もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】平方根の定義

数学

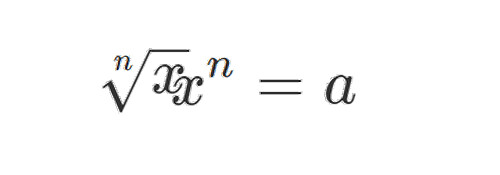
180317_03

　よく言われるのが例えば

 

  • { \displaystyle \sqrt{4} } は { \displaystyle 2 } ? { \displaystyle \pm 2 } ?
  • { \displaystyle 4 } の平方根は { \displaystyle 2 } ? { \displaystyle \pm 2 } ?

 

ですね.

 

スポンサーリンク

 

 

平方根とは

　平方根はしばしば以下のように定義されています.

 

[定義1:平方根]

　正実数 { \displaystyle a } について, { \displaystyle 2 } 乗して { \displaystyle a } になる数を 「{ \displaystyle a } の平方根」と言い, { \displaystyle \sqrt{a} } と書き表す.

 

　しかしよくよく考えてみれば { \displaystyle -\sqrt{a} } も { \displaystyle 2 } 乗して { \displaystyle a } になりますからこれもまた「{ \displaystyle a } の平方根」と考えることができます.

 

　「数」は等式関係を除いてただ一通りであることが大前提ですから, これは正しいようで定義がよろしくありません.

　その意味でも { \displaystyle \sqrt{4}=\pm 2 } は正しくありません.

　従ってしばしば以下のようにも定義されます.

 

[定義2:平方根]

　正実数 { \displaystyle a } について, { \displaystyle 2 } 乗して { \displaystyle a } になる数のうち正であるものを 「{ \displaystyle a } の平方根」と言い, { \displaystyle \sqrt{a} } と書き表す.

 

　「らしく書く」ならこれは

 

{ \displaystyle x^2=a } を満たす正実数 { \displaystyle x }

 

ですね.

　これなら { \displaystyle -\sqrt{a} } は除外されます.

 

 

n乗根

　平方根は上の通りで良さそうです, ではより一般的に { \displaystyle n } 乗根についてはどうしましょう？

 

　一般の複素変数 { \displaystyle x } の { \displaystyle n } 次方程式

 

{ \displaystyle x^n=a }　 ( { \displaystyle a } は正実数)

 

の解は, ド・モアブルにより以下となります.

 

{ \displaystyle x\equiv \zeta_k=\sqrt[n]{a} \left( \cos{\frac{2\pi k}{n}} + i\sin{\frac{2\pi k}{n}} \right) }
{ \displaystyle (k=0,1,\dots , n-1) }

 

　ようは複素数の範囲では { \displaystyle n } 個の解を持ちます.

　この { \displaystyle n } 個の複素数は定義から { \displaystyle n } 乗して { \displaystyle a } になる数です.

　従って { \displaystyle n } が大きくなれば { \displaystyle n } 乗根の候補もどんどん増えます.

 

　従って以下のように定義することになります.

 

[定義3:{ \displaystyle n } 乗根]

　任意の正実数 { \displaystyle a } について,

 

{ \displaystyle \zeta_0 = \sqrt[n]{a} }

 

を { \displaystyle a } の { \displaystyle n } 乗根と言う.

 

 

nが奇数のとき

　そもそも { \displaystyle -\sqrt[n]{a} } という数は, { \displaystyle n } が奇数のとき { \displaystyle n } 乗すると { \displaystyle -a } になってしまいます.

　そう言う意味では定義2の「正であるもの」も弱い定義と言えるかもしれません.

　存在しないことが明らかのため寧ろ都合が良いとも取れますけどね.

 

 

〆

　ただ説明するだけなら「{ \displaystyle n } 乗根とは { \displaystyle \sqrt[n]{a} } のこと」と言ってしまえば楽ですが, 相手次第では例えばまだ複素数について習っていなかったりしますからね.

 

thetheorier