もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

(数学)「マイナスでかける」を掛け算なしで理解してみる

数学

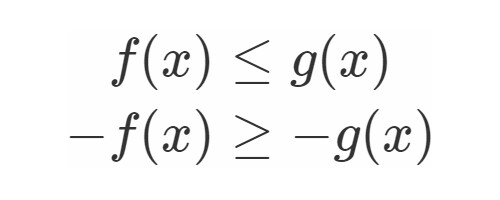
 160519_15

　多くの方にとって当たり前の事でも, そうでない方には目から鱗…となってくれたら嬉しいですね.

　等号付き不等式でやりますがそうでなくともただの等式でもOKです.

　今回はいつもより「緩め」です.

 

[Contents]
 

 

事前準備

thetheorier.hatenablog.com

　先日紹介しましたが単位元, 逆元の定義は最低限理解しておきます.

　今回は端折りますが以下になります, 分からない人は等式だけ覚えておくか, 次の「式変形」まで飛ばしましょう.

 

[単位元]

　半群 { \displaystyle (G, *) } について, { \displaystyle G } の任意の元 { \displaystyle a } について

{ \displaystyle a*e = e*a = a }

を満たす { \displaystyle G } の元 { \displaystyle e } がただ一つ存在するとき, { \displaystyle e } を単位元と言う.

 

　群 { \displaystyle (G, *) } について, { \displaystyle G } の任意の元 { \displaystyle a } について

{ \displaystyle a*a' = a'*a = e }

(但し { \displaystyle e } は { \displaystyle (G, *) } の単位元)を満たす { \displaystyle G } の元 { \displaystyle a' } が, { \displaystyle a } に応じてただ一つ存在するとき, { \displaystyle a' } を{ \displaystyle a } の逆元と言う.

　特に二元演算 { \displaystyle * } が加法 { \displaystyle \times } であるとき, 逆元 { \displaystyle a' } を特別に { \displaystyle -a } と書き表します.

 

　今回は一般的な代数系なので, 加法について { \displaystyle e = 0 }, 乗法について { \displaystyle e = 1 } であるとしてかまいません.

 

　また上記エントリにあるThm3も理解しているとします, ここで改めて書いておきます.

 

環 { \displaystyle R } の任意の元 { \displaystyle a, b } について

{ \displaystyle (-a)b = a(-b) = -ab }

 

　これを利用すると, 特に { \displaystyle (-a)b = -ab } について { \displaystyle a = 1 } とすれば

{ \displaystyle (-1)\times b = -(1\times b) = -b }

ですね.

 

 

式変形

　例えば

{ \displaystyle -x \leq 1 }

を変形してみましょう.

{ \displaystyle x + (-x) = 0 } 　…(1)

ですから, { \displaystyle -x } の加法逆元は { \displaystyle x } です.

　同様に { \displaystyle 1 } の加法逆元は { \displaystyle -1 } ですね.

　よって両辺に { \displaystyle x } を足し, 次に { \displaystyle -1 } を足すと

{ \displaystyle x + (-x) \leq x + 1 }

{ \displaystyle \Leftrightarrow 0 \leq x + 1 }　…((1)より)

{ \displaystyle \Leftrightarrow x+1 \geq 0 }　…(左辺と右辺をひっくり返す)

{ \displaystyle \Leftrightarrow x + (-1) + 1 \geq (-1) + 0 }　…(両辺に { \displaystyle -1 } を足す)

{ \displaystyle \Leftrightarrow x \geq -1 }

 

, これで「{ \displaystyle -1 } でかける」行為をせずに変形できました.

 

　{ \displaystyle -1 } 以外でもやることは同じです, 例えば { \displaystyle -3x ＞ 2 } なら, { \displaystyle 3x + (-3x) = 0 } より { \displaystyle -3x } の加法逆元は { \displaystyle 3x } ですから,

 

{ \displaystyle 3x + (-3x) ＞ 3x + 2 }

{ \displaystyle \Leftrightarrow 0 ＞ 3x + 2 }

{ \displaystyle \Leftrightarrow 3x + 2 ＜ 0 }

{ \displaystyle \Leftrightarrow 3x + (-2) + 2 ＜ (-2) + 0 }

{ \displaystyle \Leftrightarrow 3x ＜ -2 }

 

となります.

 

 

〆

　まぁ逆元を引っ張り出してる時点で「掛け算なしで」なのか微妙なところですが…

　今回は「不等式の式変形」について混乱されてる方がいるのを見て書いてみた次第です.

 

　エレガントなやり方ではないですが理解するための一つの方法としてどうぞ.

 

thetheorier