もう一人のY君

主にiPhoneのショートカットアプリのレシピやTipsなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】一通りであるべきなのに複数の表記がある有理数

数学

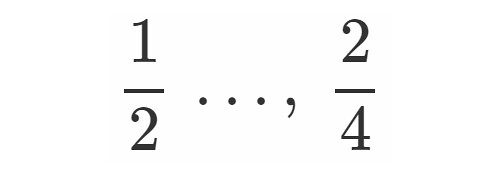
rational number unique

　疑問に思う方も少なからずおられるでしょう.

 

スポンサーリンク

 

 

数は一通り

　自然数がそうであるように, 一つ一つの数はただ一通りに表されるのがその定義の一つです.

 

　参考までにペアノの公理を書いておきます.

 

 

[公理：自然数(ペアノ)]

　数の集まり { \displaystyle \mathbb{N} } が自然数であるとは, 次の5つの条件を満たすものである.

 

  1. 　{ \displaystyle \mathbb{N} } は { \displaystyle 1 } を要素として含む. { \displaystyle 1\in\mathbb{N} }
  2. 　任意の { \displaystyle x\in\mathbb{N} } に対し, { \displaystyle x+1 } に対応する { \displaystyle \mathbb{N} } の要素が存在する.
    　このとき { \displaystyle x } に対する { \displaystyle x+1 } を「{ \displaystyle x } の後者」などと呼ぶことがある.
  3. 　{ \displaystyle 1 } が後者となる要素は存在しない.
  4. 　{ \displaystyle x+1=y+1 } ならば { \displaystyle x=y } .
  5. 　{ \displaystyle \mathbb{N} } は以上の1～4を満たす集合のうち最も小さいものである. つまり { \displaystyle \mathbb{N} } の任意の真部分集合で上記1～4を満たすものは存在しない.

 

　ここで自然数の「はじまり」として { \displaystyle 1 } にしましたが, これを { \displaystyle 0 } としても問題ありません.

　この辺はどんなカテゴリで, どのような目的で使用するかによるため, どちらが正しい・間違っているということではありません.

 

 

　今回注目するのは公理で言うところの 3 に相当します.

　公理とはその取り決めの通り, それを論証や証明などを行わずに真(=正しい)であるとし, 以降行う諸々の演繹, ひいては結論を導くための「大前提」として扱います.

　従ってこれらは疑問を持つ必要なく認めましょう, 不満であればそれこそ「不満である理由」を説明し, かつこれが公理でないことを証明しなければなりません.

 

 

複数の表記で表せる数

　自然数はその公理から明らかに一通りで表せられます.

 

　しかし例えば有理数はその限りではありません.

 

　{ \displaystyle \frac{1}{2} } に等しい数として例えば { \displaystyle \frac{2}{4} } や { \displaystyle \frac{3}{6} } , それこそ「分数」の世界まで広げてしまえば { \displaystyle 0 } でない任意の実数 { \displaystyle k } について

 

{ \displaystyle \frac{a}{b}=\frac{ak}{bk} }

 

ですから(有理数であっても似たようなものですが), いくらでも等しいものが存在します.

 

　写像をご存知であれば「全射だけど単射でない」ようなものです.

 

　例えば関数 { \displaystyle y=x^2 } の値が { \displaystyle 1 } となるような { \displaystyle x } が { \displaystyle -1, 1 } の2通りあるように, 一つの値を与える「独立変数」「引数」が複数存在し得る状況にあります.

 

 

同値関係が解決してくれた

　そんな不合理を解決したのが同値関係という考え方です.

　この言葉を知らなくても図形の相似や合同をご存知ならその仲間のようなものと思って構いません(寧ろそれをまとめたものですが).

 

　すなわち, ある集合 { \displaystyle S } とその要素を用いた条件 { \displaystyle \sim } を用いて次のように考えます.

 

[定義：同値関係]

　集合 { \displaystyle S } とその上で定義される条件 { \displaystyle \sim } が以下を満たすとき, { \displaystyle \sim } を { \displaystyle S } 上の同値関係と言う.

 

　任意の { \displaystyle a, b, c\in S } に対して

  1. { \displaystyle a\sim a }
  2. { \displaystyle a\sim b } ならば { \displaystyle b\sim a }
  3. { \displaystyle a\sim b } かつ { \displaystyle b\sim c } ならば { \displaystyle a\sim c }

 

 

　具体的には, 今回であれば整数 { \displaystyle a, b, c, d }  ( { \displaystyle b, d\neq 0 } ) について次のように定めます.

 

　整数 の直積 { \displaystyle \mathbb{Z} } の直積 { \displaystyle \mathbb{Z}\times\mathbb{Z}\backslash\{0\} }

 

{ \displaystyle (a,b)\sim (c,d) \,\, \Leftrightarrow \,\,ad=bc }

 

　２つの有理数を通分した分子同士で定義したようなものですね.

 

 

同値＝同じとみなす

　結果的にこれが同値関係になるかは練習問題にするとして, こういった定義に何を見出すかというと, 「本来等しくないものを同じとみなす」ということにあります.

 

　例えば先に挙げた { \displaystyle \frac{1}{2} } { \displaystyle \frac{2}{4} } は別の数を用いているので姿は異なりますが, 上の { \displaystyle \sim } の定義より

 

{ \displaystyle 1\times 4 = 2\times 2 }

 

ですから { \displaystyle (1,2)\sim (2,4) } となります.

 

　ご存知の通り { \displaystyle (1,2)\sim (c,d) } となる { \displaystyle (c,d) } はもっとたくさんあります.

　なのでそのうちの一つを代表してそれと同値であるものだけを集めた集合を作ることができます.

　これを同値類と言います.

 

[定義：同値類]

　集合 { \displaystyle S } とその上に定められた同値関係 { \displaystyle \sim } について, 次の集合を同値類と言う.

 

{ \displaystyle [(a)] := \{x | x\sim a \} }

 

　厳密には「集合」と「類」は明確に分かつべき言葉ですが今回は端折ります.

　また問題のない範囲で { \displaystyle [(a,b)] } などとすべきところを { \displaystyle [a,b] } と略記することがあります(以降は略記で書きます).

 

　今回の話で言うなら例えば { \displaystyle [1,2] = [2,4] } が成り立つことは明らかでしょう.

 

　そして(現代)数学の都合の良いことは, こういった数でないものを対象として扱ってしまう柔軟さにあります.

　つまりこの同値類であれば, 等しいもので重複するものはありません, よってペアノの公理の 3 に適合するのです.

 

[定義：商集合]

　集合 { \displaystyle S } とその同値関係 { \displaystyle \sim } について, 次の集合を商集合と呼ぶ.

 

{ \displaystyle ^S/_\sim := \{[a] | a\in S\} }

 

　それっぽく書いたんですが { \displaystyle S/\sim } でも構いません.

 

　この商集合を, 我々が普段読んでいる自然数や整数と同じ扱いにすれば良いわけです.

 

　また, この商集合に自然な加法・乗法を定義することにより環(=加法・減法・乗法が可能な代数系)を成します, これを「商環」と呼びます.

 

 

　この商環 { \displaystyle (S/\sim, +, \times ) } であれば, 分数や有理数といった, 一つの値に対して複数の表記が可能な集合でも一意性を保つことが可能です.

 

 

〆

　解釈を変えれば, これは整数についても言えることです.

　また小数と分数についても一定の説明が可能になります(極限値については流石に無理ですが).

 

thetheorier