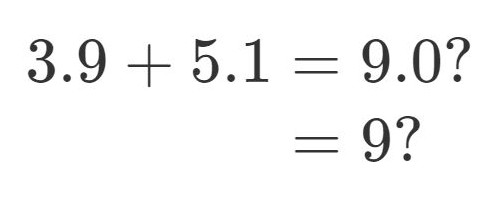
数日前から話題になった話ですね.
有効数字を入れるべきかどうか
姪っ子の小3算数テストの採点結果。.0の有効数字に意味があるというのに全く訳がわからない。 pic.twitter.com/dOUIOYzUg5
— kennel (@kennel_org) 2016年11月16日
今回の話題のネタはこちらですね.
注目されるべきは, 既に件のツイートの返信でも指摘されている通りでまだ有効数字を習っていない学年であるということです.
小数自体はまさにこの小学3年から習っているようですね1.
本題では,
教育指導の難しさ
数学をはじめとする学問の一部では, 初めからいきなり体系そのものを教えることは非現実的です.
例えば四則演算すらままならない学年でいきなり代数系がどうの, 写像がどうの, 群だ環だ体だと言っても仕方ありません.
教育する上では, 既知の概念から一部を取捨してまずそこを教えざるを得ません.
その際生まれる「取捨の外の世界」を彼らが知ったとき, 或いは指摘されたとき, 我々, 特に教師はどのように対応するべきなのか…が一番問われることだと考えます.
つまり「それ」を不正解とするのか, 取り敢えず正解にしておいて「それはまだ習ってないから」等々と一言加えるのか…
従って, このような不都合自体は, いつの時代になっても必ず生じる, 已むをえないものだと僕は思っています.
考えるべきは, その時どう対応するべきかです.
これは何も掛け算の順序や有効数字だけではありません.
例えば倍数は自然数でしか考えないと思い込んでいる方はたくさんおられるでしょうが, 同時にそんなことは全くないことをご存じの方も多いと思います.
これは実際には「まず自然数の中で考えてみる」という方針であって, 「自然数でしか定義されない」わけではありません.
解釈の相違が, 謝った認識へと繋がっていくのです, そしてその原因は個々人の思いこみや勘違いであったり, 教師の教育の仕方であったり原因は様々です.
蛇足ですがこういう難しさを考えると僕は小中高の教師への道を進む気にはとてもなれませんでした, 彼らの学術レベル・そして各教育課程に自分が合わせられる自身が無かったからです.
知の無知
我々大人, 或いは(少なくとも今回であれば)有効数字を既に学んだ学生は, 「有効数字のことを知っている」という一種の思いこみがあるからこそ, 有効数字の存在を前提にあれやこれやと論じますが, 当の小学三年の児童たちは有効数字の存在を知らずして解答したと考えるのが妥当です.
個々人で得ている学術レベルは違いますし, まして今回のように学年での相違についてであれば尚更「そちらに合わせて」評価, 議論しなければ意味がありません.
つまり, 有効数字を習っていない子・学年の児童に対して有効数字についてあれこれ言っても無意味ですし, 同時に有効数字について知っている我々に対して「有効数字であるかどうが重要である」ことなど, 説明するまでも無いのです.
今回の問題で, じゃあ児童に「有効数字だから意味があるんだよ, だから君の解答は正解だよ」と言っても, 彼はこう答えるでしょう, 「有効数字って何?」.
有効数字であることが問われているのか?
これだけ書いておいて今更なんですが, そもそもこの問題が「有効数字を問うているのか」という疑問も残ります(と思ったらこれはリプライで指摘されていますね).
とはいえ言うまでも無くこの学年では有効数字など習っていませんから, 答えはノーです.
従って強いてどちらにすべきか…と問われたら僕は「9」だと思いますが, 何度も書いた通り彼等は有効数字のことを知りませんから, 「9.0」も正解にしておくのが無難でしょう.
そもそももう一つ, 「彼(彼女)は有効数字のつもりで書いたのか?」という疑問も湧いてきます.
話が壮大になっていく
こういう話題でよくあることなんですが, 一事を以て万端を知る…な雰囲気になってしまわないように気を付けたいという点です.
現にそのような例があるとはいえ, そのような事例が通例になっているとはこの時点では何も確定していません.
しかしこれだけで当たり前のように一般論に繋げて論じてしまえる方がいらっしゃいますが.
因みにとある脳科学の専門家の方がこのように指摘されています.
「小数点問題」「かけ算の順序」「たし算の順序」問題はトリビアルに意味がない
茂木健一郎 - 小学校の算数にまかり通っている「奇習」は、子どもたちに対する「虐待」である - Powered by LINE
確かに同意する一面もありますが, このような考えは指摘されている「奇習」と変わらないのではないでしょうか?
すべての生徒が習うとは限らないとはいえ例えばいつか触れる「行列」や「ベクトル」はまったくトリビアルではありません.
いつかトリビアルでない対象, 空間, 概念が出てくるのが教育課程上の数学の運命ですから, 小学校で学ぶ内容を「トリビアル」で切り捨てるのは, まさにそれがトリビアルであると知っているが故の「知の無知」, 「思考停止」としか言いようがありません.
どこまでトリビアルとするべきか, どこから「この先にまだ深く大きな世界が広がっているか」を, ハッキリではないにしろその片鱗を見せてあげるのか, これは教育者に常に求められる大事な役目であり, かつ難題だと思うのです.
僕らにとっては当たり前でも, 彼(彼女)らにとっては当たり前ではないのです.
〆
児童はもちろんのこと, 我々がやってしまいがちなのは「思いこみ」です.
一度そう習い, 聞かされれ, 疑問に思わず納得すればそれが間違いであったり不十分であったとしても簡単には疑いません.
掛け算の順序に気を付けなければならないのは何故か.
小数点以下の0を消すべきか残すべきか
, その「何故か」「どうするべきか」について後腐れ無く説明するのが正しい教育だと思います.
でなければ後になって「(本人にとっての)例外」が現れた途端にできなくなり, 最悪「数学嫌い」に繋がります.
世の「数学嫌い」の一因はここにあると思います, 実際嫌いな方は「あの時は~って習ったのに」と思ったことはないでしょうか?
算数はもちろん, 数学で常に認識していなければいけないことは「その先の世界が存在しうること」です.
そこで終わりじゃありません.
いづれにしろ議論の対象が狭いために, いくらでも話を広げられ, それに沿った賛否両論で溢れています.
僕のこの主観も一部を切り取って書いたものに過ぎません.
[参考]
1. 文部科学省 「小学校学習指導要領解説 算数編 平成20年6月」
