もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】符号と記号の違い

数学

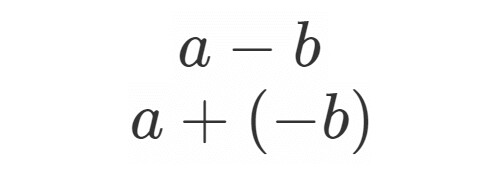
170415_00

　特に四則演算, プラスとマイナスについてです.

 

 

プラスやマイナスは符号か記号か

　どちらが正しいのか…と言われれば「どちらも正しい」が正解です.

　どう違うのかは「それをどう使っているか」によります.

 

 

演算についておさらい

　以前にもちょくちょく紹介していますが, そもそも演算というのは基本的に(二元)演算を指します, つまり代数学的な表現をするなら集合 { \displaystyle G } の直積 { \displaystyle G\times G } について,

 

{ \displaystyle G\times G\,\to\,G \\ \,(a, b)\,\to\,c=a*b }

 

となる { \displaystyle * } を二元演算とし, 組 { \displaystyle (G, *) } を代数系と呼びます.

 

 

記号としてのプラス, マイナス

　この { \displaystyle * } が(演算)記号としての記号を指します.

 

　例えば { \displaystyle 1+2 } や { \displaystyle 3-4 } で使われている { \displaystyle +, - } は(演算)記号と言えます.

 

 

符号としてのプラス, マイナス

　代数系には各演算における逆元を元に定めた演算, つまり一般に言うところの減法と除法があります.

　この2つは基本的にはそれぞれ加法, 乗法から定義しています, つまり加法, 乗法における逆元

 

{ \displaystyle a+a'=a'+a=0_e \\ aa''=a''a=1_e }
(※重複を防ぐため { \displaystyle a'' } としています)

 

, この定義に基づき, 加法逆元 { \displaystyle a' } を { \displaystyle -a }, そして乗法逆元 { \displaystyle a'' } を { \displaystyle a^{-1} } と書き, 以下のように減法, 除法を定義します.

 

{ \displaystyle a-b:=a+(-b) \\ a\div b:=a\times b^{-1} }

 

　この { \displaystyle -b } で使われている { \displaystyle - } が符号に相当するわけです.

 

　対象の数が正であることを強調するために書く { \displaystyle +a } といった表記もこれに相当します, したがって

 

{ \displaystyle +a+b }

 

と書かれている場合前者の { \displaystyle + } は符号, 右は(演算)記号ということになります.

 

　もう一つ例を挙げれば, 先程の減法の定義に出てきた

 

{ \displaystyle a+(-b) }

 

の場合, { \displaystyle + } は(演算)記号, { \displaystyle - } は符号ということになります.

 

thetheorier