こんにちは, @the_theorierです.
先日地上波でサマーウォーズをやっていたお陰で再び「モジュロ演算」等々の言葉が出てきたので, 所詮僕が理解している範囲でちょっと突っ込みを入れたいと思います.
モジュロ演算について
まずさっそくのこれですが, 数学の世界でモジュロ演算とかそういう呼び方をしたり聞いたりはしたことがありません.
一般には日本語で「合同式」, 英語でcongruence, あるいは congruence equationと書きます.
定義としては基本的には, 整数Z上の任意の整数 a, b の差 a-b が整数 m の倍数であるとき,
a ≡ b (mod m)
などと表します.
このとき m に相当するものを「法」, 英語でmoduloと呼ぶため(mod はこの省略したものです), これを発音して「モジュロ」, 「モジロ」と呼んでいます.
因みに法は除数と同じ意味です, カテゴリによって呼び名が異なるだけです.
またここで合同式の定義を「a を m で割った余り」とするケースがありますが, 厳密には正しくありません.
例外として例えば 1 ≡ 3 (mod 2) や -1 ≡ 3 (mod 4) などを説明できないからです.
しかし a≧b≧0 と制限すれば b は a を m で割った余りであることに他ならないため, 教育課程上「狭い定義」で進めるために起こる誤解です.
より突っ込めば, 上で書いた定義も更に拡大した定義が存在します, イデアルを用いたもので完全に大学数学のレベルですが.
そしてこの合同式, 日常で使わない…なんて声がありますがとんでもありません.
時間や曜日で例えば「1日と8日は同じ曜日」…なんてことはこの合同式の考えに他なりません.
またこれは合同式に限らない話ですが,
0は無か, 虚数は実在しないのか
これも全く違います.
どちらも発見時やその地域などの文化などでそのように解釈されたことはありましたが数学という学問上での解釈とは異なります.
例えば数学者である高木貞治氏は著書で下のように主張しています.
数学上の概念はすべて抽象的であるが,整数も勿論その例に洩れない.前に言うた整数の体系の内の一対一の対応は,各整数にその直後の整数を対応せしめるとき,各整数はその直前の整数に対応することを背景として,それを公理として立てたのであるが,我々はその対応を抽象的に考察するのであって,直前・直後というような具体的の意味は全く抽き去るのである.だから,我々の整数は,物の数でもなく,物の順序を示すものでもない.しかし,物の数を示すためにも,物の順序を示すためにも,なお一般に,物の標識(符牒)としても用いられる.
は加法の規準として,我々が任意に整数の体系の中から取り出した一つの整数である.それは,無を示すものではない.整数を計量に応用するならば,我々の鼻が一つ・目が二つであることが,整数
で表現されるのが便利であろうが,それは言語の習慣に過ぎない.事実は,我々が常用の言語に順応して,我々の記号
を零, 一,二と呼ぶことにしたのである.
-高木貞治 数の概念/序 - Wikisource より引用-
「0は加法の基準として, 我々が任意に整数の体系の中から取り出した一つの整数である」, ここにすべてが集約されていると思います.
現在数学, こと代数学においては, 演算が定義された集合(=代数系)は基本的には, その集合とそれに付加された演算がどのような「構造」を持っているか, そこに関心があり, 既に我々が知っている「0」や「1」がある…ということはせず, 例えば集合の任意の元 a に関して
a * e = e *a = a
を満たす元 e が存在する場合, これを以て e を単位元とし, 「0」(演算によっては「1」)に相当するものを「特徴付け」ます.
従って「0」はあくまでもその集合の元としてきちんと「存在している」のです.
こういった抽象的な表現がまさに数学の難しいところなんですけどね…
さてもう一つ, 虚数, つまり「実数でない複素数」は実在しない数なんでしょうか?
逆に, 実数はどのように存在しているんでしょうか?
紙に書いたから分かる?でもそれは虚数だって同じです.
長さや位置として表現できる?でも下のようにして実数 R については距離をユークリッド距離 √(a^2 + b^2) としたR^2空間, そして複素数 C についても同じ距離を定めれば, R^2, Cの両者の空間は同じ構造であるとみなすことが出来ます(数学ではこのような関係を「同型」と言います).
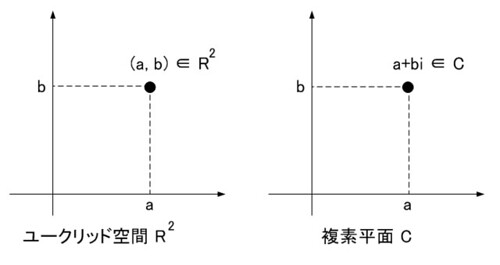
もちろん無限遠点等々を考えると全く同じとは言わないんですけどね.
また, 数学では「より大きな空間から対象を評価する」ことがよくあります.
特に対象の正体が分からないとき, 取り敢えずそれも含めた上で, 条件を満たす最小の構造体を評価します.
例えば自然数だけでは引き算は出来ません, なので「任意の自然数の元を使って引き算が出来るように対象を増やす」ことをします.
我々は既にその増やすべき対象がなんであるか, つまりそれが負数のことであることは知っていますが.
少なくともそういった構造を定める以上, 例外(矛盾)があるかどうかを確かめるのは重要なことです, 1-2の結果が本当にあるのか…という問題は, 2-1が簡単に出来る以上, 負数を知らないその人は「(現時点では)観測できないけれども存在を認めざるを得ない」のです.
「認める」までは悉く否定されてきたわけですけどね, ある意味地動説天動説です.
このように, 対象が観測できない場合でも, それが存在するものとして構造体系に含めるのを「内部対称性」と言うそうです.
上記では自然数に対する負数でしたが, 同じことは実数に対する虚数も同じことです.
物理科学で複素数を扱う場合がありますが, これも内部対称性の良い例です.
虚数という「観測できない世界」が具体的にどうであるかはさておき, 構造体系に矛盾が無ければ, それを取りこんで考えて問題ないわけです.
どうせ必要なのは観測できる値だけなのですから.
また例えば学校で実数係数の二次方程式の解の公式を学びますね.
しかしよく考えれみれば, あれは係数の組み合わせ次第では虚数解になりえます.
学んだ当初は実数解である場合のみ触れるので意識することは少ないですが, いつか嫌でもその状況にお目見えします.
そのとき我々は実数解でないそのケースを認めるべきかどうか…となります.
否定するならば, それは解の公式として価値があるのか, 疑うべきかもしれません.
そうでないならば, 解の公式を経て虚数解になりうることを, つまりは虚数の存在を認めなければなりません.
いうなれば数学も一つの言語であり, 等しく抽象的な存在です, 虚数の実在性を疑うならば, あなたは「言葉が存在すること」を, どうやって証明するべきでしょうか?
教育課程, 数学の必要性
ある意味で, 現在数学は既にかなり成熟しており, とことん抽象化され, それぞれが体系として整っています.
なのでそれを学べば手っ取り早いんですが, 当然ながらそんなことを高校いや中学, 小学校でやった所で分かるはずもありません.
なので教育課程上はまず具体的な計算などを主軸におき, それをこなすことでそこに法則が存在するであろうことを理解します, ボトムアップというヤツですね.
そして中学高校と進学するにつれ, 文字を使ったり証明をしたりと, 少しずつ体系や論理そのものから着手し, そこから一つ一つの結論に辿りつくことになります, これはボトムアップに対してトップダウンですね.
数学者として…いや数学でなくとも, 求められるのは両方というわけです, どちらかに偏っていては宜しくありません.
抽象的な話しか出来ない人は相手にちゃんと伝わってるか怪しいですし, 具体的な話しかできない人は例外に立ち会った時に対応できるか怪しいのです.
個人的には相変わらずの受験偏向ぶりはどうかとは思いますが, 総合的に見ればこのボトムアップ→トップダウンのやり方はやむを得ないと思います.
むしろこれは現代数学に至る流れそのものでもあるからですね.
現在数学の体系がはじめから演繹, 論理によって生まれたわけではなく, 一つ一つの事実の集合から法則を見出し, 後にそれを公理体系などとしたわけです, 代数系, 特に自然数の定義の歴史はまさにそれを物語っています.
しかしこのボトムアップ→トップダウンの流れにおいて, 前者に拘り過ぎていると, いざトップダウンの世界に入ったときに混乱したり, 中々理解できずに嫌いになってしまう…ということが往々にしてあるわけです.
度々話題になっている乗法の可換性にしても, (あれは多分「問題文をちゃんと理解しているか…」という意味があるからでしょうが)順序に凝り固まったまま進学し, 後にそれが障害となって理解を妨げることになりかねません.
数学というのはもっと自由で都合の良い世界なんですけどね…
従って基本的に数学は演繹的推論ですが, だからといって帰納的推論を否定することはできません.
そもそも数学が必要であるか…について例えば論理的思考が養える云々という主張もありますが, 結局のところ何が必要なのか不要なのかは「その時にならないと分からない」ですよね.
従って必要ない…という理由もまた無いわけです, 「他人のその時の結果論」に依存して自分の人生, 取捨選択をしても, 誰も責任は取ってくれません.
〆
因みに数学(mathmatics)の語源はμαθηματαであり, 「学ぶべきもの」と意味します, つまり学問そのものです.
現在ではより細分化され, 意味が異なるものとなってしまいましたけどね.
また, 我々が使っている数学の「数」, これは「ことわり」「論理」「運命(計数の赴く所は必然…ということから)」という意味も持っていたそうで, 古代中国ではむしろそちらの意味で使われていたようです.
数学は抽象的で分かりづらいとよく言われ, 実際そうですが, 逆に言えば抽象的だからこそ, 色んな分野に「落とす」ことができるのです.
ちょっとうまくまとめられないので今回はここまでです, では.
