もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】色んな「ほとんど整数」

数学

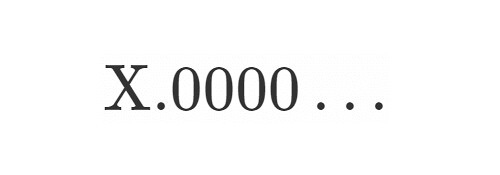
almost integer

　数学は必ずしも厳密な研究ばかりでなく, たまには今回のような遊び感覚というか趣味というか, そんな範疇のものもあります.

 

 

スポンサーリンク

 

 

ほとんど整数

　ほとんど整数とは,

 

整数ではないが整数に限りなく近い数

 

のことを言います.

　小数表示にして1.0000345とか12.99999954637といった数になるもののことです.

 

　どの程度近いのもであるべきかは特に決められていません.

 

 

ほとんど整数の有名な例

　これまでにほとんど整数となる数はたくさん見つけられています.

 

 

ほとんど整数であることが数学的に証明できる例

　例えば円周率 { \displaystyle \pi } には { \displaystyle \frac{22}{7} } や { \displaystyle 3+\frac{\sqrt{2}}{10} } といった近似値があるので, これを用いて簡単にほとんど { \displaystyle 0 } ないしほとんど { \displaystyle 3 } である数が求まります.

 

{ \displaystyle \pi - \frac{22}{7} \approx -0.0012644892\dots }

{ \displaystyle \pi - \frac{\sqrt{2}}{10}\approx 3.0001712973\dots }

 

　また貴金属比の累乗も, 簡単にほとんど整数を与えます.

　例えば黄金比 { \displaystyle \varphi = \frac{1+\sqrt{5}}{2} } の累乗はほとんど整数となります.

 

 

　かの鬼才ラマヌジャンは, パっと見てとてもほとんど整数にすら見えない数 { \displaystyle e^{\pi\sqrt{163}} } を与えました.

　これは { \displaystyle 262537412640768743.9999999999992500\dots } という非常に精度の高いほとんど整数です.

 

 

極限から評価する例

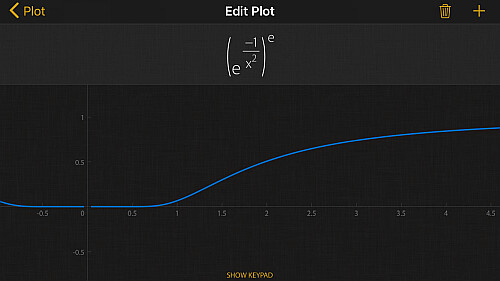
171107_01

　また例えば極限 { \displaystyle \lim_{x\to\infty}\left(e^{-\frac{1}{x^2}}\right)^e } は { \displaystyle 1 } に収束しますから, { \displaystyle x } に十分大きな数を与えるだけでほとんど { \displaystyle 1 } となります. 

 

　貴金属比の累乗同様, このようにトリビアルなケースもあります.

 

 

今回見つけたもの

　数学的に証明されたものもあれば, たまたま見つけただけでそうであることを証明できていないものもたくさんあります(多分後者の方が多いでしょうかね).

 

　ここ数ヶ月, 時間を見つけてコツコツ探しました, モノによっては精度がよくありませんが.

　調べるにあたっては普通の関数電卓だととても手間なので先日紹介したArchmedes Calculatorを使用しています.

 

Archimedes Calculator

Archimedes Calculator

  • Patrick Pijnappel
  • 教育
  • 無料

※価格は記事執筆時のものです. 現在の価格はApp Storeから確認ください.

 

blog.thetheorier.com

　その場ですぐ修正・再計算できるのでとても便利です.

 

 

　なお { \displaystyle \pi } は当然ですが円周率, { \displaystyle e } はネイピア数になります.

　オイラー数 { \displaystyle \varphi } も使いたかったですがこれは追々考えたいと思います.

 

 

ほとんど2017,2018,2020

　まずは今年と来年, そして(たまたま見つけただけですが)オリンピックにちなんで { \displaystyle 2020 } に近いものです.

 

 

{ \displaystyle \sqrt[266]{e^{2017}+2017^{266}}\approx 2017.0063070327\dots }

 

{ \displaystyle e^{\pi\sqrt[10]{6950}}\approx 2016.9946594594\dots }

 

{ \displaystyle e^{\pi\sqrt[12]{40774}}\approx 2016.9992332937\dots }

 

{ \displaystyle e^{\pi\sqrt[13]{98844}}\approx 2018.0009589363\dots }

 

{ \displaystyle e^{\pi\sqrt[11]{16870}}\approx 2019.9908013813\dots }

 

{ \displaystyle \frac{\pi^{\log_e{2018+\pi^{e+12}}}}{2018\pi + 30980e}\approx 2019.9997398303\dots }

 

 

上記以外の「ほとんど整数」

　上記を除くほとんど整数です.

　小数点直下から { \displaystyle 0 } ないし { \displaystyle 9 } が並ぶ数で分けておきます.

 

 

2桁

 

{ \displaystyle \sqrt[5788]{\frac{\pi^{2018}+2018^{2018}}{2018e^{2018}}}\approx 10.0064456510\dots }

 

 

3桁

 

{ \displaystyle \sqrt[16]{\frac{2018^{e\pi}}{2018^e+2018^\pi}}\approx 13.0006480659\dots }

 

{ \displaystyle \sqrt[2018]{\frac{e^{2018}+2018^\pi}{2018^e+2018^{265}}}\approx 1.0006873107\dots }

 

{ \displaystyle 2\cdot 25^e\approx 12618.9993654206\dots }

 

{ \displaystyle \pi^{e\sqrt[17]{2018}}+e+\pi\approx 135.9992510879\dots }

 

{ \displaystyle \frac{2^\pi +4}{e}-e\approx 1.9997638476\dots }

 

{ \displaystyle \frac{2^\sqrt[3]{3}}{e}\approx 0.9996912709\dots }

 

{ \displaystyle \frac{2^\sqrt[3]{219}}{e}\approx 23.9998772057\dots }

 

{ \displaystyle \frac{2^\sqrt{94}}{e}\approx 304.9998396442\dots }

 

{ \displaystyle \frac{2^\sqrt{134}}{e}\approx 1122.9997271698\dots }

 

{ \displaystyle 10\frac{2^\sqrt{92}}{\pi}\approx 2456.0002837344\dots }

 

{ \displaystyle \frac{2^\sqrt{110}}{\pi}-\frac{e-1}{10}\approx 456.9998915729\dots }

 

{ \displaystyle \frac{2^\sqrt{132}}{\pi}\approx 915.0007803770\dots }

 

 

4桁

 

{ \displaystyle e^2-3\pi^3+\sqrt{243\pi}\approx -57.9999528274\dots }

 

{ \displaystyle \frac{3e+2\pi^2}{2e+\pi^e}\approx 0.9999402386\dots }

 

{ \displaystyle \frac{\pi^2+e-1}{\pi-e+1}-\pi\approx 4.9999081520\dots }

 

{ \displaystyle \frac{2^\sqrt{107}}{e}-\frac{e-1}{10}\approx 478.0000221825\dots }

 

 

11桁

 

{ \displaystyle \frac{\pi^{2017}+2017^{300}}{\pi^{2017}+2017e^{2017}}\approx 1.0000000000045758\dots }

 

{ \displaystyle \frac{\pi^{2018}+2018^{300}}{\pi^{2018}+2018e^{2018}}\approx 1.0000000000014565\dots }

 

 

〆

　きちんと証明できるかどうかを除けば, 手間さえかければ結構見つかるんじゃないかと思います.

　上記も既にあるようなものを参考にある程度「当たり」をつけて見つけたものです.

 

　興味のある方は他にもっと良いものが無いか探してみましょう.

 

thetheorier