もう一人のY君

主にiPhoneのショートカットアプリのレシピやTipsなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【ショートカット】ユークリッドの互除法

iOS iOS-iOS12 iOS-ショートカット

181110_14

　今回はユークリッドの互除法によって2数の最大公約数を求めるショートカットを作ってみました.

 

ショートカット

ショートカット

  • Apple
  • 仕事効率化
  • 無料

※価格は記事執筆時のものです. 現在の価格はApp Storeから確認ください.

　レビュー時のバージョン　：　v2.1.1

 

スポンサーリンク

 

 

最大公約数の考え方

　基本的な性質として, 2数 { \displaystyle a,b } の最大公約数 { \displaystyle \text{gcd}(a,b) } について次が成り立ちます.

 

{ \displaystyle \text{gcd}(a,b) = \text{gcd}(a,-b) = \text{gcd}(-a,b)  }

{ \displaystyle \text{gcd}(a,b) = \text{gcd}(b,a) }

 

　これらを考慮し, 処理中の2数は非整数, かつ { \displaystyle a\geq b } として計算することにします.

　これを揃えないと面倒なので.

 

　一旦整理すれば後はそれほど難しくありません.

　{ \displaystyle 0\leq b\leq a } となったため, 割り切れるショートカットと同様に

 

{ \displaystyle \left[\frac{a}{b}\right] }

 

を求めます.

　この値はつまり商であり, 元の { \displaystyle a} から { \displaystyle \left[ \frac{a}{b} \right]b } だけ引いた結果が正値最小剰余となり, 次の数式へと引き継がれます.

　商とその剰余を改めて { \displaystyle a\geq b } の関係となるよう並び替え, 同じ操作を繰り返せばいつか剰余が 0 になります, その時最大公約数が求まることになります.

 

　ただ問題なのは「2数が与えられたとき, ユークリッドの互除法が何回の式変形で終わるのか」がわからないため, 後述しますが今回は10回で固定としています.

　この数字が2数に対応して変えることができれば, 組み合わせ次第では無駄な処理を省略できます(いずれ調べるつもりです).

 

 

フロー

　ではフローを見てみましょう.

 

 

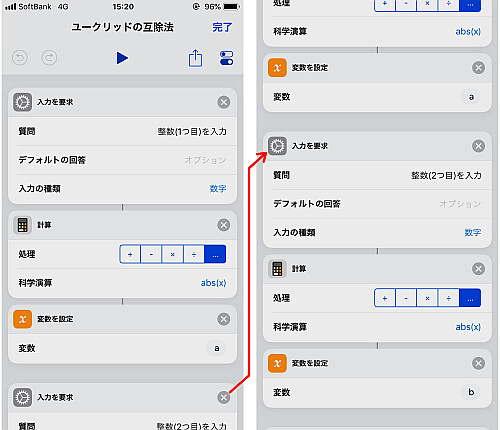
181110_15

　まず整数の入力を要求し, 絶対値をとってaとし, これを使用します.

　同じものをもう一つ作ります.

 

 

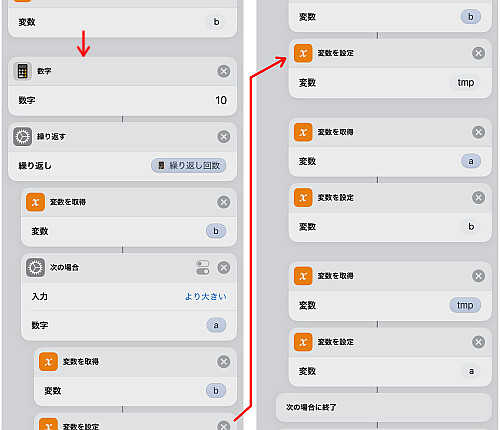
181110_16

　「繰り返す」のアクションを配置し, 回数は上記の通り今回は10回固定とします.

　その後2数 a, b の大小を比較し, { \displaystyle a\geq b } となるように変換します.

 

 

181110_17

　a, bの大小を確定させたら { \displaystyle \frac{a}{b} } および { \displaystyle \left[ \frac{a}{b} \right] } の値を計算します.

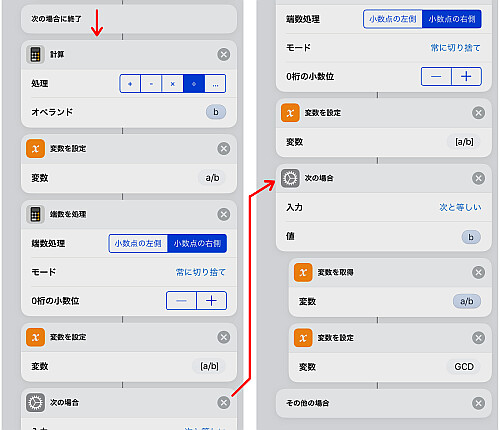
　もし { \displaystyle \left[ \frac{a}{b} \right] } が { \displaystyle b } と等しいならば, 互いに倍数の関係にある可能性があるため, 商 { \displaystyle \frac{a}{b} } を最大公約数の候補として変数 GCD に代入します.

 

 

181110_18

　そうでない場合今度は { \displaystyle b } 自身をチェックします.

　もし { \displaystyle b = 2 } より小さい, つまり繰り返しでの最初の処理から { \displaystyle b=1 } ですから　{ \displaystyle a } が最大公約数で決まりです.

　従って GCD に { \displaystyle a } を「追加」します.

　以降 GCD に代入する操作は「変数を設定」でなく「変数に追加」を使うことで配列化します.

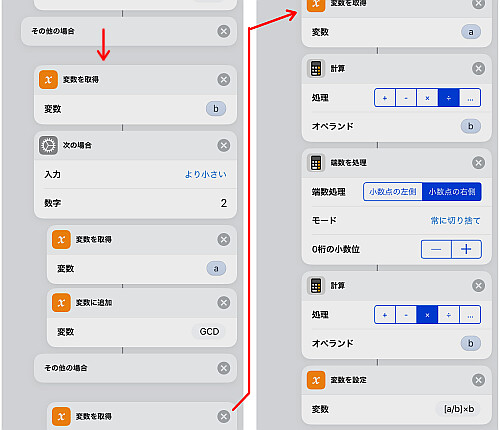
　さて { \displaystyle b=1 } でない場合は何倍かして余りを求め, これらの操作をまだ続ける必要があるということになります.

　そこでまず { \displaystyle \left[ \frac{a}{b} \right]b  } を求めます.

 

 

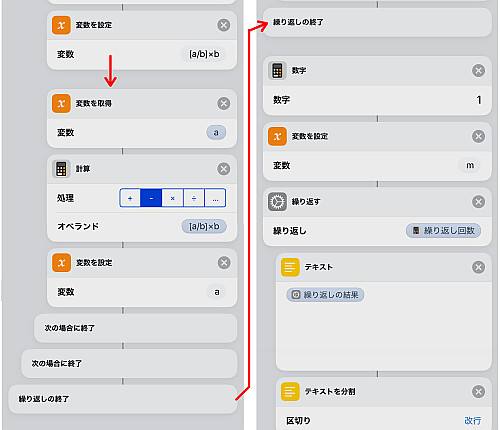
181110_19

　更にこれを { \displaystyle a } で引き, 結果 { \displaystyle \left[  \frac{a}{b}  \right]b-a  } を改めて a に代入し, この新しい a と b とを用いて再び繰り返します.

　これによって配列 GCD にはユークリッドのアルゴリズムで最大公約数まで順に小さくなった数の列が続き, 以降0が続く配列を成します.

 

　上の繰り返しを抜け, 初期値1とした繰り返しの媒介変数mを用意し, 最初と同じ繰り返し回数(今回は10)で GCD の列から最大公約数となっている数を取り出します.

　

 

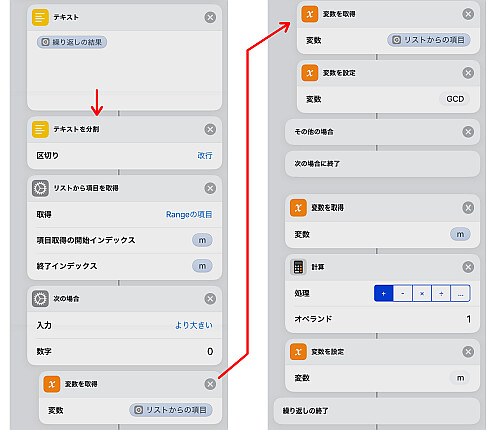
181110_20

　配列となった変数から項目を取り出すため, 一度「テキスト」に配列を置き, 「テキストを分割」で改行分割します.

　その後 m 個目の項目を「リストから項目を取得」で取り出し, 各自0より大きいかどうかをチェック, 正しいなら改めて変数 GCD に代入します(配列としてのGCDと同じ名前にしてまったのでややこしいですがこのGCDは配列のGCDと別物です).

　その後mを1つ足して次へ移行します.

　これで最後には配列GCDの0でない最後尾, つまり最大公約数が取り込まれることになります.

 

 

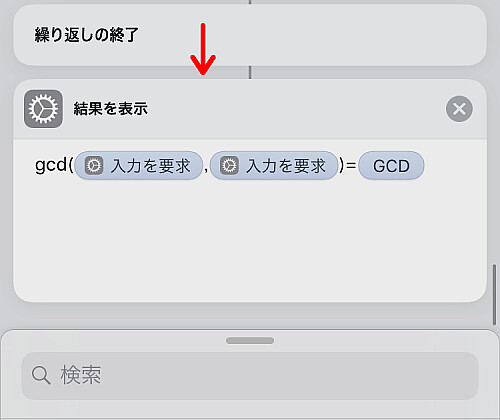
181110_21

　最後に「結果を表示」などで確かめます.

 

 

実行

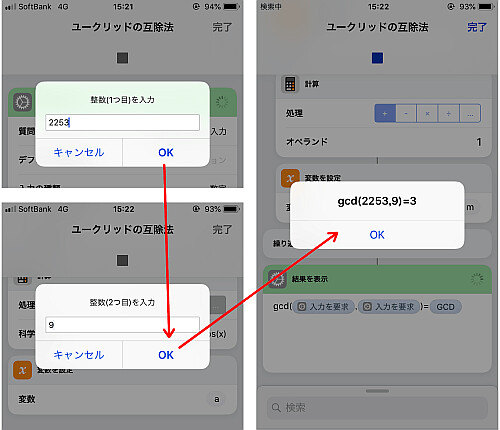
181110_22

　実際に実行し, 結果が正しいことを確かめます.

 

 

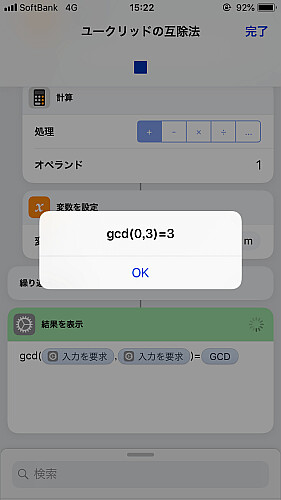
181110_23

　他方が0の場合も正しい値が出ています.

 

 

〆

　もっとスッキリ作れたらいいのですがそこはセンスのない僕の問題です.

　とはいえ互除法は歴史があるにも関わらず処理速度が比較的早いアルゴリズムです, こんな冗長な内容でも処理は結構早いです.

　ただ大きな値を用いると正しい結果が得られない時があります.

 

thetheorier