
先日シンプルな合同式のショートカットを作りましたので今回は累乗の状態から計算するショートカットを作りました.
※価格は記事執筆時のものです. 現在の価格はApp Storeから確認ください.
レビュー時のバージョン : v2.1.1
スポンサーリンク
予め整除する
今回は法を5以上の素数 に限定します.
累乗 の底
や指数
はどのような数になるか分かりません.
例えば を計算するなら,
により
を計算した方が楽に決まっています.
またフェルマーの定理より, ならば
ですから, 指数についても条件付きで簡約化できます.
よってまずはこの2つの性質より を簡単にし, その後計算することにします.
フロー
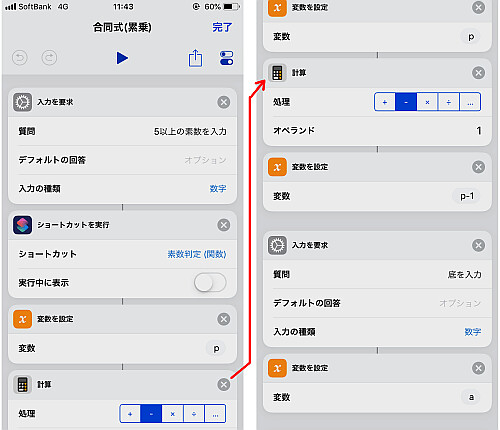
まずは法の入力を要求し, 素数判定を行います.
先日紹介した通り, 関数化した素数判定のショートカットを起動させます.
問題なければ素数自身が帰ってきますのでこれを変数pで置きます.
また後の演算用にp-1の値を計算しておきます.
底 a の値もこのタイミングで入力を要求しておきましょう.
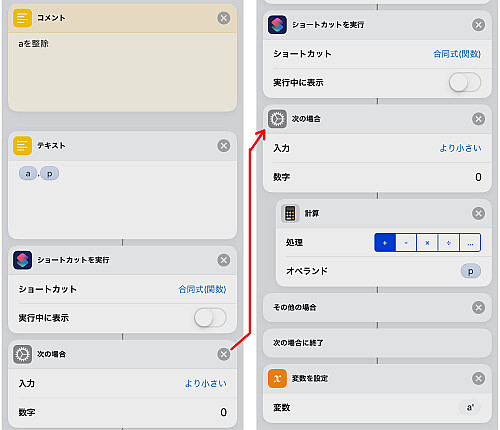
まずは底 a を法 p で整除します.
先日の関数のやり方に従い決められたフォーマットに値を直し, 関数にした合同式のショートカットを呼び出します.
今回の合同式の関数は先日紹介したものと同様のため絶対値最小剰余で帰ってくるため, 結果が0より小さい場合法pだけ足してあげる必要があります.
こうして得られた結果を新たな底として変数 a' に代入します.
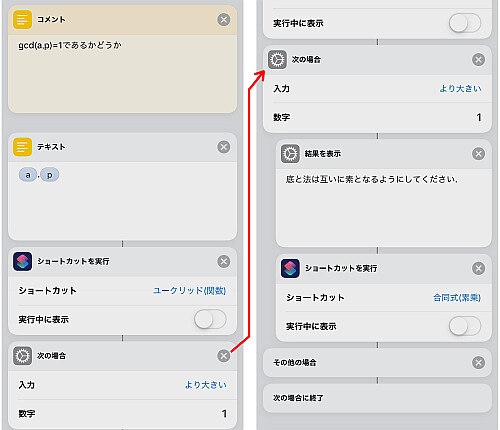
続いてフェルマーの定理に伴い, である必要があるためやはり関数として作ったユークリッドの互除法のショートカットを呼び出し,
を計算します.
もし結果が1より大きいならば今回の目的に外れるため, エラーメッセージを添えて「ショートカットを実行」でこのショートカット自身を実行することで初めからやり直します.
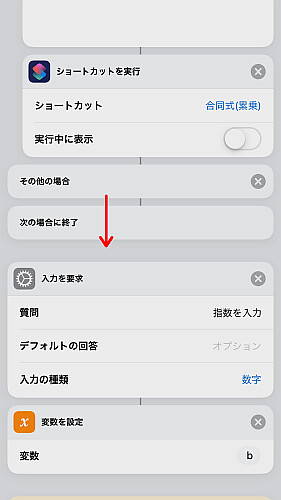
底の整除が終わったので次は指数です.
まず「入力を要求」で数を入力させ, 変数 b で置きます.
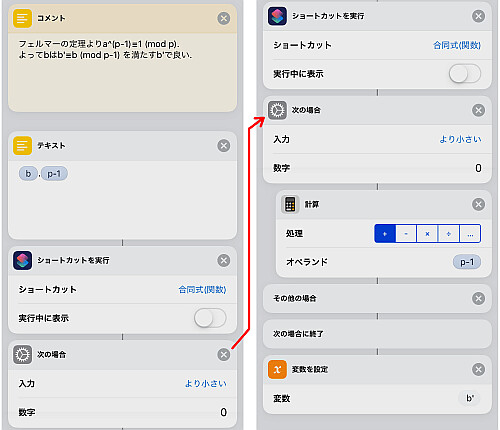
底の場合と同様, まず b を整除します.
但しフェルマーの定理より でなく
で整除することに注意します.
得られた結果を改めて b' とします.
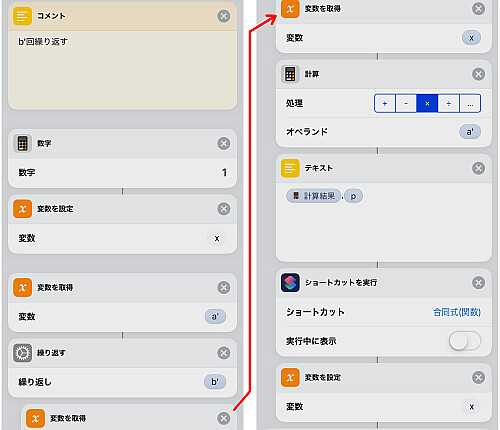
あとは を計算して法で整除したいところですが, 既に整除したとはいえそれでも
を一気に計算するのはリスクがあります.
そこで を順にかけ, そのたびに整除することを
回繰り返す操作を行います.
処理速度は落ちますが大きな数を扱うならば避けられません.
繰り返しの結果得られたものを x(初期値1) でおき, これと とをかけて関数である合同式にかけます.
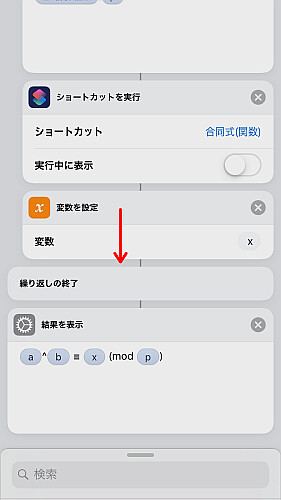
繰り返しを終えた後の x が求める答えとなっているはずです.
実行
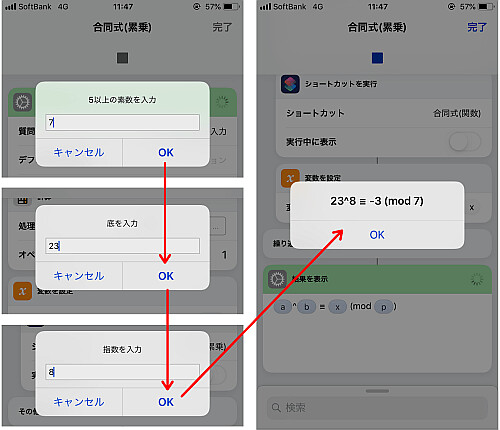
実行してみると, 正しいことが確認できます.
〆
法が大きい程, 繰り返し処理も多くなるためどうしても遅くなります.
それでも手計算よりは速いですね.


