もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【ショートカット】合同式を計算するショートカット(改造版)

iOS iOS-iOS12 iOS-ショートカット

181121_00

 

blog.thetheorier.com

　やはりこのやり方は冗長でした, 投稿後しばらくしてもっと簡単に出来ることに気づきました.

 

ショートカット

ショートカット

  • Apple
  • 仕事効率化
  • 無料

※価格は記事執筆時のものです. 現在の価格はApp Storeから確認ください.

　レビュー時のバージョン　：　v2.1.1

 

スポンサーリンク

 

 

商を利用する

　律儀に合同式の定義に従う必要はありませんでした, ようは結果が正しければ良いのです.

 

　法 { \displaystyle m } と整数 { \displaystyle a } が存在するとき, 除法の定理より

 

{ \displaystyle a = qm+r }

 

を満たす整数の組 { \displaystyle (q, r),\,(0\leq r\lt m) } がただ一つ存在します.

 

　知りたい値は { \displaystyle r } であり, 従って { \displaystyle q } が分かれば

 

{ \displaystyle r = a-qm }

 

により求まります.

 

　では { \displaystyle q } はいくつなのか, 除法の定理の式を変形すれば

 

{ \displaystyle q = \frac{a-r}{m} }

 

, { \displaystyle r } は { \displaystyle 0\leq r\lt m } でしたから

 

{ \displaystyle \left[q\right] = \left[ \frac{a}{m} \right] }

 

, この { \displaystyle \left[ q \right] } が事実上の商であり, 右辺はこれまでの整数論関連のショートカットでも頻繁に登場した式ですね.

 

　但し結果を絶対値最小剰余にしたい場合は床関数(ガウス関数)でなく四捨五入にする必要があります.

 

 

フロー

　ではフローを見てみましょう.

 

 

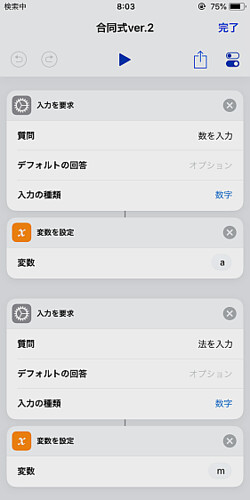
181121_01

　まず整数と法の入力を要求するのは前回と同じです.

 

 

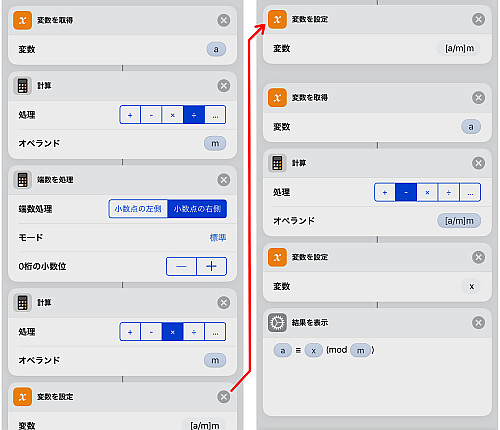
181121_02

　続いて変数 a を呼び出し, m で割って端数処理を行います.

　これまでの端数処理は切り捨てでしたが今回は結果を絶対値最小剰余にするために

 

  • 端数処理：小数点の右側
  • モード：標準
  • 0桁の小数位

 

にします.

 

　計算した値を a から引けば求める答えが得られます.

 

　前回のショートカットはアクション数26個でしたが, 今回は17個と約7割にまで抑えることができました.

　しかも今回はループ処理も一切無く, 四則演算と端数処理のみです.

 

 

実行

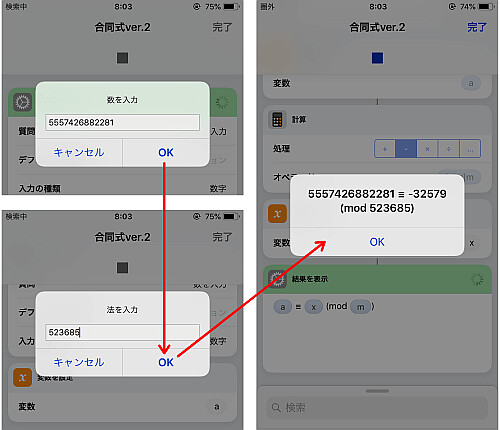
181121_03

　内部の処理数も減り, アクション自体も処理に負担がかからないもののみとなった結果, 全体の処理も前回に比べ圧倒的に軽くなりました.

　画像のような { \displaystyle x\equiv 5557426882281\pmod {523685} } の計算もあっという間です.

 

 

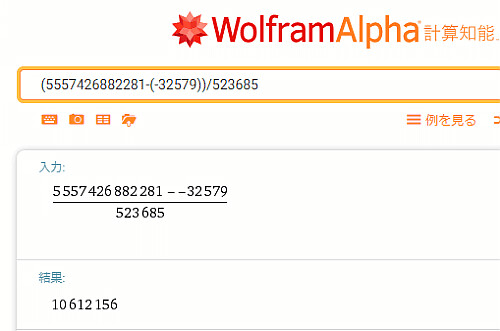
181121_04

　検算しても { \displaystyle 5557426882281-(-32579) }{ \displaystyle =5557422720860 }{ \displaystyle =523685\times 10612156 } で合っているようです.

 

 

〆

　ショートカットにあるアクションのうち, スクリプティングに属する一番の「天敵」は「繰り返す」です.

　繰り返し回数が増えれば増えるほど, 高級言語のそれ以上に処理にかかる時間が顕著に長くなってしまうため, できるだけ使用は避けたいのです.

 

　得られる結果は同じでも組み方によってより速くも遅くもできるのは面白いですよね.

(できればこっちを先に思いつきたかった…)

 

thetheorier