
先日の素数判定ショートカットより処理時間を改善したものを作ってみました.
※価格は記事執筆時のものです. 現在の価格はApp Storeから確認ください.
レビュー時のバージョン : v2.1.1
スポンサーリンク
偶数を排除
前回の素数判定は与えられた数 に基づいて 2 から
までの自然数すべてについて割り切れるかどうかをチェックしていました.
は仕方ないにしてもそれ以降の偶数は処理の無駄です.
そのためまず で割り切れるか判定し, 以降は
以上の奇数で割り切れるかを判定することで処理時間の削減を行いました.
フロー
まずは関数から紹介します.
2で割り切れるかどうかと3以上の奇数のそれについての構造は同じですが, メインフロー全体のことを考えて前者のみ関数として別に作りました.
2倍判定関数
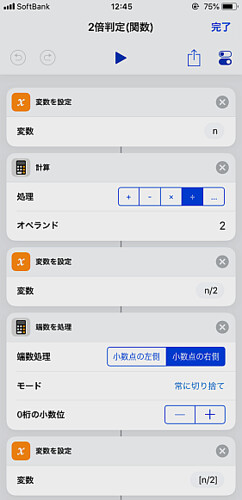
関数を適用する直前に与えられた入力を「変数を設定」で変数 n に渡します.
いつものようにこれを用いて および
を作ります.
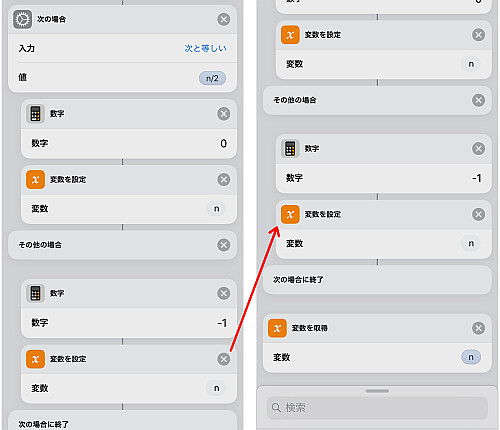
2数が一致すれば n は 2 で割り切れることを意味します.
今回はその場合 0 を返し, そうでない場合は -1 とします.
関数は以上です.
メイン
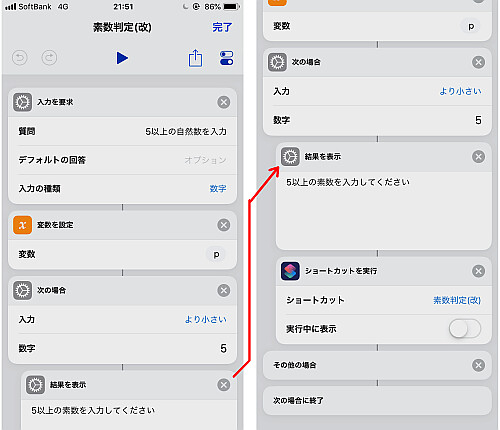
ではメインのフローについてです.
まず素数判定する値の入力を要求し, 5未満の場合はエラーとしてショートカットをやり直させます.
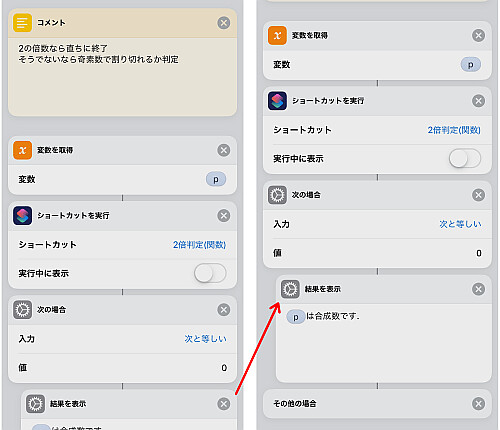
ここからメインの処理になります.
まず2で割り切れるかどうかをチェックします.
入力を要求で得た値を再び取得し, 先程の2倍判定のショートカットを適用します.
0が帰ってきた場合は2で割り切れるという意味であり, はじめの処理により値 p は 5以上の数ですからこの時点で pは5以上の偶数であることは明白のため, 素数でないことがわかります.
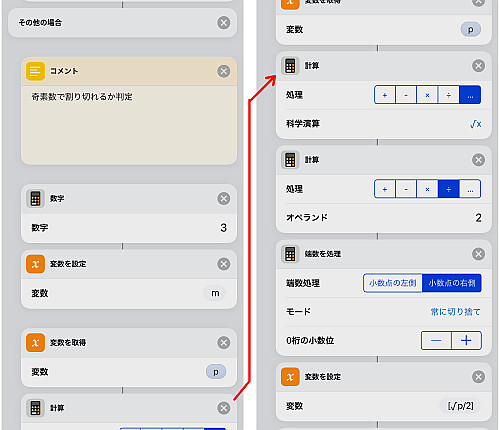
以上を通過した値 pは少なくとも「5以上の奇数」ということになるので, あとは3以上の奇数で割り切れるかどうかを判定します.
3を初期値として変数 m を与え, 繰り返し回数として を計算します.
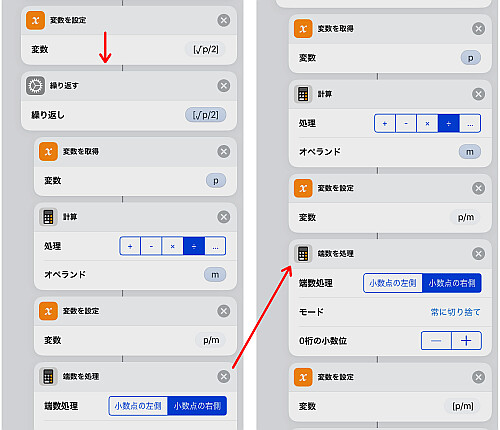
上記の繰り返し回数を用いた「繰り返し」を置き, および
を計算します.
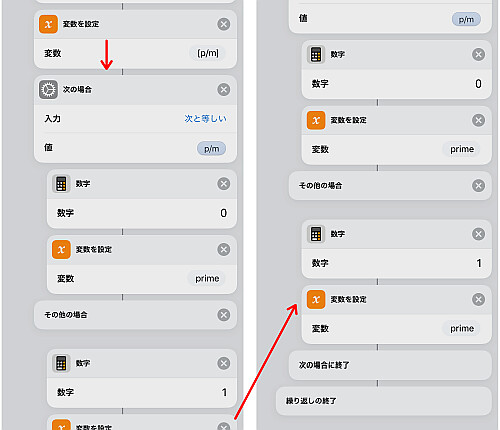
2数が一致したら, 素数判定用変数として prime を置き, 0 を代入, 一致しなければ 1 を代入します.
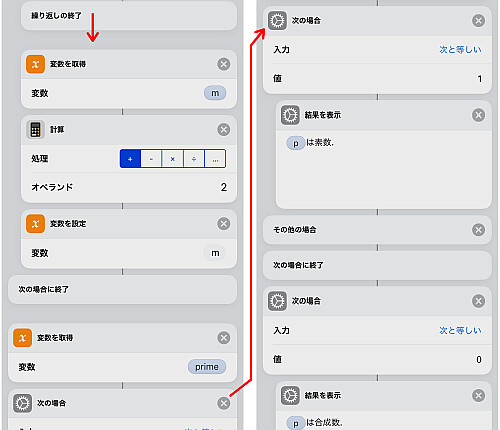
最後に m を2つ足して繰り返しに戻ります.
これで繰り返しが終わり, prime が1なら素数, 0のままなら合成数ということになります.
変数 prime の値に応じて結果を表示して終わります.
〆
この手法だと, 繰り返しの回数が約半分になることがわかります.
実際前回と処理時間(秒)を簡単に比較したところ以下になりました.
| p | 旧 | 新 |
|---|---|---|
| 997 | 2.4 | 1.6 |
| 9973 | 3.8 | 2.5 |
| 99991 | 9.2 | 4.4 |
| 999983 | 28.4 | 15.1 |
| 9999991 | 79.2 | 38.2 |
値が大きい程, 処理時間もちょうど半分くらいに改善しています.
今回は2の倍数だけ特別扱いしたわけですが, 素数判定などを組み合わせて必要な数だけにすればもっと改善するかもしれません.


