もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU

箱ひげ図の定義は一つではない？

数学

 160217_00

　以前別サイトに書いていたものを少し修正したものです.

　※スマホで閲覧される方は, 横向き画面をおすすめします.

 

[Contents]
 

 

箱ひげ図とは

　箱ひげ図とは, 統計学の標本調査で用いられる指標の一つであり, 主に

  • 最小値
  • 第一四分位数
  • 中央値(メジアン, 第二四分位数)
  • 第三四分位数
  • 最大値

の5つの指標を視覚的に評価するために用いられます.

 

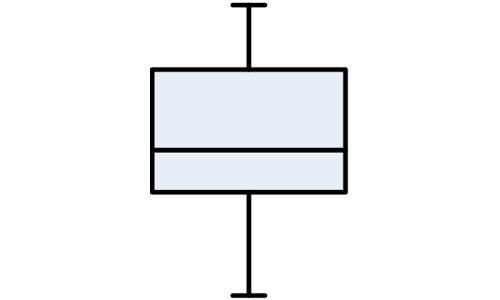
160217_00a

　こんな風に描かれ, 中央が「箱」, そして上下に「ひげ(髭)」が伸びているいるように見えることから箱ひげ図と呼ばれますね.

　箱ひげの大ざっぱな書き方は同じで

  • 上にある「ひげ」の上端が最大値
  • 「箱」の上端が第三四分位数
  • 「箱」の下端が第一四分位数
  • 下にある「ひげ」の下端が最小値

であり, 中央値は場合によって書かれたり書かれなかったりですが, 書く場合は箱内部に横線を引きます(記事トップ画像のような感じ).

　細かい書き方も特に厳しいきまりがあるわけではありません, 記事トップのようなシンプルなものから, Googleスプレッドシートのように箱内部を塗りつぶしたりと色々です.

　最大値, 最小値の部分に横線を加えるかどうかも違いますね, あった方が分かりやすいと思いますが, 目的次第でしょうね.

 

 

各指標の定義

　最大値, 最小値, 中央値は簡単ですね.

 

 

最大値

　標本の要素のうち, 最も小さくない要素のことです.

　なぜここで「最も大きい」としないかは, 例えば標本が 1, ,2, 3, 3 の場合, 3と3は"等しい"を除いた大小の比較ができないからです.

 

 

最小値

　最大値と同様, 標本の要素のうち, 最も大きくない要素のことです.

 

 

中央値

　標本を大きい順, または小さい順に並べたとき, ちょうど真ん中に来る要素のことです.

　中央値はメジアン, 或いは第二四分位数と呼ばれることもあります.

　例えば標本が 1, 2, 4, 5, 5の場合, 標本数は5なので中央値は3番目の4になります.

 

　しかし例えば標本数が偶数だと, 真ん中の要素…を考えることができません.

　この場合は前後の要素の相加平均を中央値とします.

　例えば標本が 1, 2, 4, 5 の4つの場合, 2つ目と3つ目の要素である2, 4の相加平均である

{ \displaystyle \frac{2+4}{2}=3 }

が中央値になります.

 

 

四分位数

　データ解析の分野で高校数学にも採用されるようになった箱ひげ図ですが, それに欠かせない指標がそもそもこの四分位数です.

　おおまかに言えば標本の分布を4分割するための, その値が四分位数になります.

　記号としては小さい方から順に { Q_{1}, Q_{2}, Q_{3} } と書き表します.

　問題はその定義が一通りでない…ということですね, 順に紹介しましょう.

 

　因みにいづれの場合も第二四分位数 { \displaystyle Q_{2} } は中央値で一致しているため, 第一, 第三四分位数 { \displaystyle Q_{1}, Q_{3} } のみ記述します.

　また標本数は { \displaystyle n } とし, 標本が小さい順に

{ \displaystyle x_{1}, x_{2}, x_{3}, ..., x_{n} }

という風に与えられているとします.

　また { \displaystyle \lfloor x\rfloor }は床関数, { \displaystyle \lceil x\rceil }は天井関数です.

　床関数は日本国内ではしばしば「ガウス記号」と呼ばれ, { \displaystyle [ x] } と書き表しますが後述するように天井関数に触れる部分があるので今回は床関数を採用します.

 

 

四分位数からわかること

　こういったものを考えるのですから, 計算して意味があるということです.

　定義の前に簡単に説明すると

 

  • { \displaystyle Q_{3}-Q_{1} }の値はデータの散らばり具合を表しているひとつの指標である
  • { \displaystyle Q_{3}-Q_{1} }の値が大きければ大きいほど, データの散らばり具合が大きいと言える
  • { \displaystyle Q_{3}-Q_{1} }は四分位範囲と呼ばれ, データの散らばり具合を表す数値としてより適している

[参考]日本評論社「数学セミナー2013年1月号　『数学I』の四分位数・箱ひげ図に悩む　何森 仁」

 

 

定義A : 検定教科書

　ちょっと古いですが2013年度の時点で調べたものです.

(nが偶数のとき)

　{ \displaystyle Q_{2} }で分割された標本2グループそれぞれの中央値が, 小さい方から順に { \displaystyle Q_{1}, Q_{3} } と定められます.

 

(nが奇数のとき)

　{ \displaystyle Q_{2} }を除外して分割した標本2グループそれぞれの中央値が, 小さい方から順に { \displaystyle Q_{1}, Q_{3} } と定められます.

 

 

定義B : Webio辞書より

　{ \displaystyle Q_{1} = x_{f},　但し　f := \lfloor\frac{n}{4}\rfloor }

　{ \displaystyle Q_{3} = x_{t},　但し　t := n-f+1 }

 

 

定義C

　質問サイト「OK WAVE」で見つけたものですが出自は不明.

　{ \displaystyle \lfloor\frac{kn}{4}\rfloor　(k=1, 2, 3) } が整数　⇒　{ \displaystyle Q_{k}:=\frac{x_{\frac{kn}{4}}+x_{\frac{kn}{4}+1}}{2} }

　{ \displaystyle \lfloor\frac{kn}{4}\rfloor　(k=1, 2, 3) } が整数でない　⇒　{ \displaystyle Q_{k}:=x_{\lfloor\frac{kn}{4}+1\rfloor} }

 

 

定義D : 内分点による定義1

　Microsoft Excelで使われ, Wikipediaでも紹介されている定義です.

　{ \displaystyle m_{1}:=\frac{n+3}{4},　m_{2}:=\frac{n+1}{2},　m_{3}:=\frac{3n+1}{4}  }

として内分点 { \displaystyle m_{i} (i=1, 2, 3) } を定義し,

　{ \displaystyle m_{i} }が整数　⇒　{ \displaystyle Q_{i} := x_{m_{i}} }

　{ \displaystyle m_{i} }が整数でない　⇒　{ \displaystyle Q_{i} := (H-m_{i})x_{L}+(m_{i}-L)x_{H} }

{ \displaystyle (但し, L := \lfloor m_{i}\rfloor,　H := \lceil m_{i}\rceil) }

と定義します.

 

 

定義E : 内分点による定義2

　定義Dと同じ内分点を用いますが, { \displaystyle Q_{i} } の定義が異なります.

{ \displaystyle (m_{i}が整数の場合) }

　定義Dと同じです.

 

{ \displaystyle (m_{i}が整数でない場合) }

　{ \displaystyle Q_{i} }は{ \displaystyle m_{i} }番の前後の標本による相加平均になります.

 

 

定義ごとの違い

　これらすべてを比較するには, 標本数を4で割った余りで分類するのが都合がよいです.

　実際に分類してみると以下のようになります.

 

n = 4k型

 ABCDE
{ \displaystyle Q_{1} } { \displaystyle \frac{x_{\frac{n}{4}}+x_{\frac{n}{4}+1}}{2} } { \displaystyle x_{\frac{n}{4}} } { \displaystyle \frac{x_{\frac{n}{4}}+x_{\frac{n}{4}+1}}{2} } { \displaystyle \frac{x_{\frac{n}{4}}+3x_{\frac{n}{4}+1}}{4} } { \displaystyle \frac{x_{\frac{n}{4}}+x_{\frac{n}{4}+1}}{2} }
{ \displaystyle Q_{2} } { \displaystyle \frac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2} } { \displaystyle \frac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2} } { \displaystyle \frac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2} } { \displaystyle \frac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2} } { \displaystyle \frac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2} }
{ \displaystyle Q_{3} } { \displaystyle \frac{x_{\frac{3n}{4}}+x_{\frac{3n}{4}+1}}{2} } { \displaystyle x_{\frac{3n}{4}+1} } { \displaystyle \frac{x_{\frac{3n}{4}}+x_{\frac{3n}{4}+1}}{2} } { \displaystyle \frac{x_{\frac{3n}{4}}+x_{\frac{3n}{4}+1}}{2} } { \displaystyle \frac{x_{\frac{3n}{4}}+x_{\frac{3n}{4}+1}}{2} }

 

 

n = 4k+1型

 ABCDE
{ \displaystyle Q_{1} } { \displaystyle \frac{x_{\frac{n-1}{4}}+x_{\frac{n-1}{4}+1}}{2} } { \displaystyle x_{\frac{n-1}{4}} } { \displaystyle x_{\frac{n-1}{4}+1} } { \displaystyle x_{\frac{n-1}{4}+1} } { \displaystyle x_{\frac{n-1}{4}+1} }
{ \displaystyle Q_{2} } { \displaystyle x_{\frac{n+1}{2}} } { \displaystyle x_{\frac{n+1}{2}} } { \displaystyle x_{\frac{n+1}{2}} } { \displaystyle x_{\frac{n+1}{2}} } { \displaystyle x_{\frac{n+1}{2}} }
{ \displaystyle Q_{3} } { \displaystyle \frac{x_{\frac{3n+1}{4}}+x_{\frac{3n+1}{4}+1}}{2} } { \displaystyle x_{\frac{3n+1}{4}+1} } { \displaystyle x_{\frac{3n+1}{4}} } { \displaystyle x_{\frac{3n+1}{4}} } { \displaystyle x_{\frac{3n+1}{4}} }

 

 

n = 4k+2型

 ABCDE
{ \displaystyle Q_{1} } { \displaystyle x_{\frac{n+2}{4}} } { \displaystyle x_{\frac{n+2}{4}-1} } { \displaystyle x_{\frac{n+2}{4}} } { \displaystyle \frac{3x_{\frac{n+2}{4}}+x_{\frac{n+2}{4}+1}}{4} } { \displaystyle \frac{x_{\frac{n+2}{4}}+x_{\frac{n+2}{4}+1}}{2} }
{ \displaystyle Q_{2} } { \displaystyle \frac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2} } { \displaystyle \frac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2} } { \displaystyle \frac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2} } { \displaystyle \frac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2} } { \displaystyle \frac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2} }
{ \displaystyle Q_{3} } { \displaystyle x_{\frac{3n+2}{4}} } { \displaystyle x_{\frac{3n+2}{4}+1} } { \displaystyle x_{\frac{3n+2}{4}} } { \displaystyle \frac{x_{\frac{3n+2}{4}-1}+3x_{\frac{3n+2}{4}}}{4} } { \displaystyle \frac{x_{\frac{3n+2}{4}-1}+3x_{\frac{3n+2}{4}}}{4} }

 

 

n = 4k+3型

 ABCDE
{ \displaystyle Q_{1} } { \displaystyle x_{\frac{n+1}{4}} } { \displaystyle x_{\frac{n+1}{4}-1} } { \displaystyle x_{\frac{n+1}{4}} } { \displaystyle \frac{x_{\frac{n+1}{4}}+x_{\frac{n+1}{4}+1}}{2} } { \displaystyle \frac{x_{\frac{n+1}{4}}+x_{\frac{n+1}{4}+1}}{2} }
{ \displaystyle Q_{2} } { \displaystyle x_{\frac{n+1}{2}} } { \displaystyle x_{\frac{n+1}{2}} } { \displaystyle x_{\frac{n+1}{2}} } { \displaystyle x_{\frac{n+1}{2}} } { \displaystyle x_{\frac{n+1}{2}} }
{ \displaystyle Q_{3} } { \displaystyle x_{\frac{3n+3}{4}} } { \displaystyle x_{\frac{3n+3}{4}+1} } { \displaystyle x_{\frac{3n+3}{4}} } { \displaystyle \frac{x_{\frac{3n+3}{4}-1}+x_{\frac{3n+3}{4}}}{2} } { \displaystyle \frac{x_{\frac{3n+3}{4}-1}+x_{\frac{3n+3}{4}}}{2} }

 

　計算違いがあるかもしれませんがこんな感じになります.

　これらの違いは, 標本のばらつきを評価する上でどの程度影響するでしょうか？気になりますよね.

 

 

実験

　試しに下記のデータを使ってみましょう.

　データ数30, それぞれのデータをF, Gとします.

 

 123456789101112131415
F 5 5 7 8 12 15 15 25 25 28 30 32 35 40 45
G 10 10 12 12 12 12 13 20 30 32 42 42 42 45 45

 

 161718192021222324252627282930
F 45 46 52 55 60 60 65 70 72 72 78 80 85 88 90
G 45 55 55 56 58 58 58 78 80 90 90 92 92 95 95

　どのように解釈してもかまいませんよ, 例えばクラスのテスト結果とか…

 

　F, Gのヒストグラムは以下になります.

 

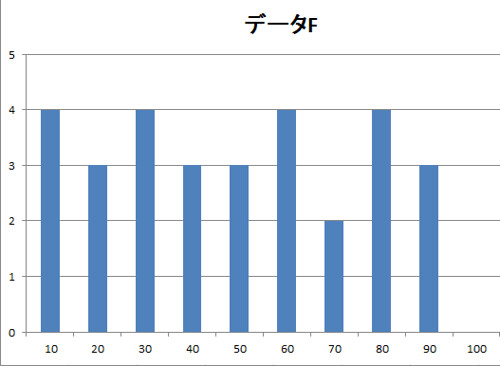
160217_01

 

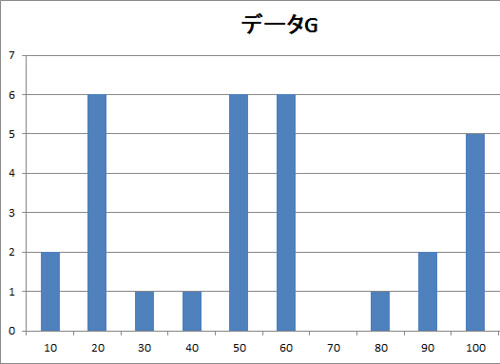
160217_02

 

　ヒストグラムからするとFの方が均一にバラついているように見えます.

　なおF, Gの分散はそれぞれ約712.672, 878.329であり, やはりGの方が大きいですね(もっと露骨にしたいところですが逆に都合のよい標本を考えるのって難しいですねw).

 

　先程の通り, 四分位数における { \displaystyle Q_{3}-Q_{1} }の値はデータの散らばり具合を評価する指標となりうるということですから, それぞれの定義における{ \displaystyle Q_{3}-Q_{1} }の位置関係を見てみましょう.

 

 

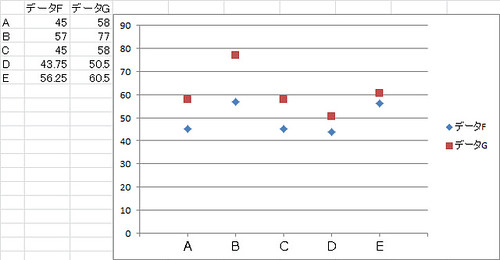
160217_03

　見ての通り, ExcelやWikipediaで採用されている定義Dと, 定義BおよびEでかなりの差が見られます.

　検定教科書の場合である定義AとDでも, データF, Gの差に違いが見られることも分かります.

　今回一致したのは定義AとCのみという結果になりました.

　対象によってはまた結果は異なるかもしれません.

 

 

検定教科書とExcelで異なるという事実

　そもそもすべての人がエクセルを日常的に使うわけでもないので強くは言いませんが, 教科書に書かれている定義と, エクセルで使用している箱ひげの定義が異なるというのは何か意図があってのことなんでしょうかね？

　折角学校で学んでも, エクセルで作成した箱ひげが習ったそれと違う…なんて本末転倒だと思いませんか？

 

　因みに以前図書館などで調べたところ, 啓林館の「新編 数学Ⅰ」ではこう触れています.

～表計算ソフトによる四分位数の計算はこれまで学んだ方法とは異なるので, 若干の値の違いが出ることがあるが, 解釈は同じなので, 全体の傾向をつかむ上では問題ない

-啓林館 「新編 数学Ⅰ」より-

　確かに全体をつかむ上では問題ないでしょうが, 複数の標本と比較する場合そういうわけにはいかないと思われます.

　多少の差による優劣の入れ替わりならばまだ許容する余地はあるでしょうが, 定義の違いによる差がどれだけ影響するかは, どうしても気になってしまうところですね.

 

　なお同時期に調べた時点では, この啓林館の書籍以外では「定義が複数存在すること」自体どこも触れられていませんでした(最近のはどうか分かりません).

 

 

〆

　この事実から考えるに, 上著の指摘の通りで箱ひげは「全体の傾向をつかむ」程度に留めるのが良いのかもしれません.

　或いは値に拘るのならば

  • 箱ひげは複数定義が存在すること
  • 定義によって値が変わりうること

を前提として評価するべきでしょう.

 

　当然ですがまったく参考にならない…ということを言いたいわけではありません.

　「そういうものだ」ということを知っておくだけで, 無用な誤解や誤りを防げる, そういうことです.

 

 

 

thetheorier