もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】無限小(または許容誤差)ε

数学

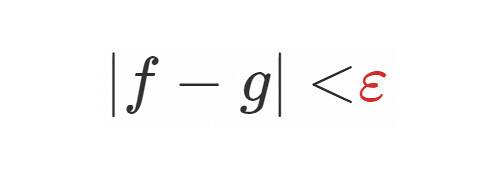
数学 無限小 infinitesimal

　今回は主に大学数学になってしまいますが高校数学以下でも重要でありうる無限小についてです.

 

 

スポンサーリンク

 

 

無限小とは

　無限小とは, 簡単に言えば限りなく { \displaystyle 0 } である, しかし { \displaystyle 0 } でない正実数を意味し, 一般的にギリシャ文字の { \displaystyle \varepsilon } を用います.

 

　実際にはこのような数は明らかに存在しません, 何故ならば このような { \displaystyle \varepsilon } が存在するならば, 任意の正実数 { \displaystyle a } について { \displaystyle \varepsilon\lt a } ですが, ここで { \displaystyle \varepsilon } が数であると認めるならば, { \displaystyle a } は実数ですから { \displaystyle a=\varepsilon } を代入して { \displaystyle \varepsilon\lt\varepsilon } となり, 矛盾してしまいます.

 

　従ってこの数は仮の存在であり, またこの時点では具体的にどんな値であるかに言及しません.

　それ故「限りなく」という枷を外せば自由ある許容誤差としても使うことが可能になります.

 

 

近似(許容誤差)

　例えば無理数である円周率 { \displaystyle \pi } は, { \displaystyle \frac{22}{7} }, { \displaystyle \sqrt{\frac{40}{3}-\sqrt{12}} }, { \displaystyle 2+\sqrt[4!]{4!} ,\dots} と言ったたくさんの近似式があります.

 

　無理数は小数表示にすると無限に数が並ぶため, その値と等しい小数を書き起こすのは不可能です.

　従ってある程度の桁数まで等しいような別の数式で代用することで, 例えば距離を測る際にそちらを使用することで計算の手間を省くわけです.

 

　「{ \displaystyle a }と{ \displaystyle b }がほとんど等しい」を意味する { \displaystyle a\fallingdotseq b } (或いは { \displaystyle a\approx b } ) は, 無限小を用いるならば言葉でなく数学として定義するならば例えば下のようにできるでしょう.

 

{ \displaystyle a\approx b \Leftrightarrow \left|a-b\right|\lt\varepsilon }

 

　そして近似値の精度, もしくは許容誤差を「評価」する場合, 正実数 { \displaystyle \varepsilon } の多寡に興味関心が向くことになります.

 

 

ε-N論法

　許容誤差は時代を経るにつれ求められる精度を増し, また現代数学に至っては「具体的な値」を超えてより抽象的な誤差・変動の評価に目を向けるようになります.

 

　関数の連続性で登場するε-N(またはε-δ)論法はその最たる例の一つであり, 高校数学までで曖昧にしてきた連続の意味を一部であれ明確にする「道具」の一つです.

 

　つまり

 

関数値の変動を { \displaystyle \varepsilon\gt 0 } に抑えることで, 変数値の変動をある制御誤差 { \displaystyle \text{N}\gt 0 } 以下に抑えられる

 

のが { \displaystyle \varepsilon -\text{N} } 論法の簡単な説明です.

 

　{ \displaystyle \text{N} } は変数値と許容誤差 { \displaystyle \varepsilon } に依存して決まり, これらに応じて大きくなったり小さくなったりします.

　目的としては

 

  • より目的の変数値に近づくほど
  • より許容誤差 { \displaystyle \varepsilon } を小さくするほど
  • 制御誤差 { \displaystyle \text{N} } が限りなく小さく抑えられる

 

ことです.

　これが不可能ならば「連続でない」わけですね.

 

 

thetheorier