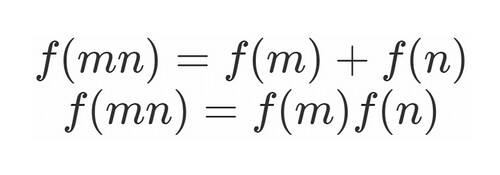
依頼があった旧サイトに投稿していたものの再投稿です.
スポンサーリンク
数論的関数とは
数学では, 我々が考える理想, 或いは「都合の良い事実」とそうでない場合が存在しえます.
関数も同じで, ある関数 を分解・展開するにおいて都合のよい環境であればそれについて深く考えたくなるものです.
その一つが数論的関数です.
先日紹介しましたが改めて少し紹介し直しましょう.
[定義:数論的関数]
数論的関数とは, 次のような関数を言う.
つまり, 正整数を定義域とし, 複素数を値とする関数である.
定義の通り, 数論的関数は非常に幅広いもののため, この時点では興味をそそられることは少ないでしょう.
加法的関数と乗法的関数
[定義:加法的関数]
互いに素である正整数 について
を満たすとき, この数論的関数 は加法的, 或いは加法的関数であると言います.
[定義:加法的関数]
互いに素である正整数 について
を満たすとき, この数論的関数 は乗法的, 或いは乗法的関数であると言います.
この2つは線形性にも似ていますね.
グラフにしてみる
前回は各々の具体的な数表でしたが今回はそれをプロットしたものを見てみましょう.
対象の各種数論的関数は前回と同じで以下となります.
以降, を異なる素因数,
を各々の指数とし,
と素因数分解されるとします.
- 加法的関数
:ビッグオメガ関数
…の素因数の, 重複を含めた総和:
例::オメガ関数
…の, 異なる素因数の個数:
例:
…の異なる素因数の総和
例:
…の素因数の, 重複を含めた総和
例:- 乗法的関数
…の正約数の個数:
例:の正約数は
なので
…の正約数の総和:
例::オイラーの
関数
…から
までの正整数のうち,
と互いに素な数の個数
例:までの正整数のうち,
と互いに素なのは
の8個なので
:メビウス関数
…が平方数で割り切れるとき
, そうでないとき
が異なる
個の素数で素因数分解されるとき,
例:は
で割り切れるので
:根基
…の異なる素因数の総積:
例:
他にもありますが今回はこの9種です.
プロット例
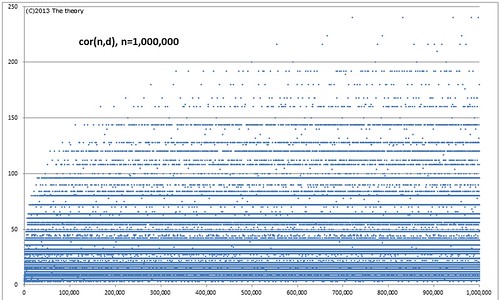
例えばこちらは横軸を , 縦軸を
としたものです.
画像の通りデータ数は まで取得しています.
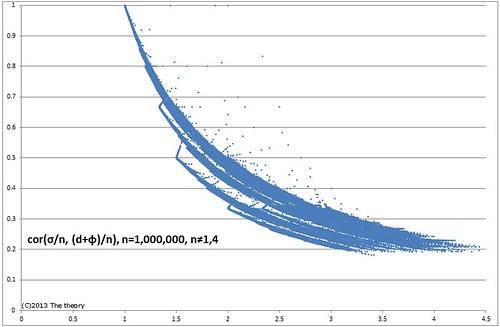
便宜上横軸と縦軸の関係として のように表記しています.
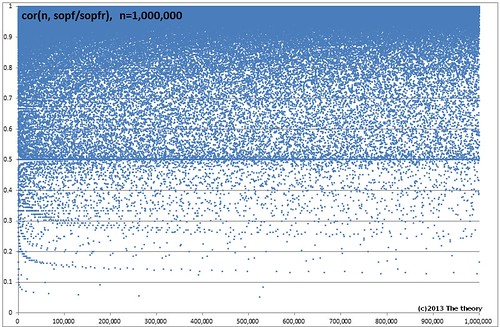
組み合わせ次第ではこのような面白い模様になります.
全部で103枚あるのでですがすべて貼ると重くなるので以降は個人的に面白いと思ったもののみ載せ, 残りは記事末にスライダを貼ってあります.
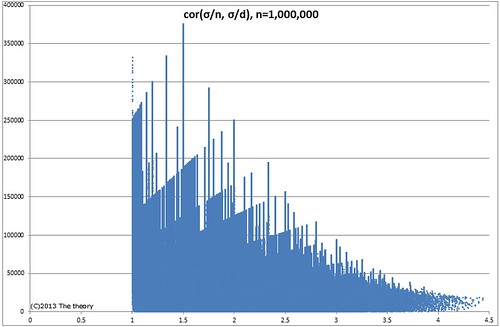
〆
何か惹かれるものがあれば嬉しいです.
上記を含めた他の組み合わせはこちら.
