もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】a≡b (mod m)ならなぜa,bをmで割った余りが等しいのか

数学

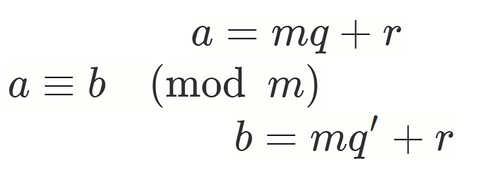
180307_00

　高校から合同式を学ぶようになってそこそこ経ちましたが, まだまだ定着するには時間がかかりそうです(そもそも何故入れたんでしょうね).

まるで堂々巡りのようなタイトルですがこんな質問があったので実際に確認してみましょう.

 

スポンサーリンク

 

 

定義

　合同式の定義は習熟度の立場から少なくとも2通りの定義があります.

 

[定義:合同式1]

　整数 { \displaystyle a,b } を整数 { \displaystyle m } で割った余りが等しいとき,

 

{ \displaystyle a\equiv b\pmod m }

 

と書き, { \displaystyle a } と { \displaystyle b } は (法 { \displaystyle m } に対して)合同であると言います.

　ここで堂々と「余りが等しい」と言ってしまっていますがスルーします(目的はこの「逆」が何故成り立つか…という話ですし).

　これは「余り」の概念から立ち入った定義と言えます, このとき整数 { \displaystyle k, k', r (0\leq r \lt b) } を用いて

 

{ \displaystyle a=mk+r }
{ \displaystyle b=mk'+r }

 

と表せますね.

　辺々引くと

 

{ \displaystyle a-b=m(k-k') }

 

となり, これは「{ \displaystyle a-b } は { \displaystyle m } の倍数」を意味します.

　この等式に余り { \displaystyle r } は登場しません(依存しない, と言います)から, いちいち余りについて考えることなく合同式を定義できることになります, それが合同式の二つ目の定義です.

 

 

[定義:合同式2]

　整数 { \displaystyle a,b } の差 { \displaystyle a-b } が整数 { \displaystyle m(\gt 0) } の倍数であることき,

 

{ \displaystyle a\equiv b\pmod m }

 

と書き, { \displaystyle a } と { \displaystyle b } は (法 { \displaystyle m } に対して)合同であると言います.

 

　これが初等整数論における合同式の定義です.

　実際にはイデアルという概念を用いた更に拡張された定義がありますが割愛します.

 

 

本題

　では本題に入りましょう, つまり以下を証明します.

 

 

　{ \displaystyle a\equiv b\pmod m } ならば { \displaystyle a,b } をそれぞれ { \displaystyle m } で割った余りは等しい.

 

 

[証明]

　仮定より, ある整数 { \displaystyle k } を用いて

 

{ \displaystyle a-b=mk } …(1)

 

が成り立ちます.

　除法の定理より, 整数 { \displaystyle q,r(0\leq r\lt m) } の組が(ただ一通り)存在して

 

{ \displaystyle a=mq+r }

 

を満たします.

　つまり「{ \displaystyle a } を { \displaystyle m } で割った余りが { \displaystyle r }」となります.

 

　これを(1)に代入して

 

{ \displaystyle (mq+r)-b=mk }
{ \displaystyle \Leftrightarrow mq+r-b=mk }
{ \displaystyle \Leftrightarrow b=m(q-k)+r }

 

, つまりこのとき { \displaystyle b } を { \displaystyle m } で割った余りが { \displaystyle r } となります.

 

　よって { \displaystyle a,b } 双方を { \displaystyle m } で割った余りが共に { \displaystyle r } で等しくなります. { \displaystyle \square }

 

 

〆

　先ほどの「拡張」でやったことを逆に辿れば良いわけですね.

 

thetheorier