もう一人のY君

主にiPhoneのショートカットアプリのレシピやTipsなどを書いています. たまに数学の記事も書きます.

　MENU

【数学】分散はなぜ絶対値でなく二乗するのか

数学

人気記事

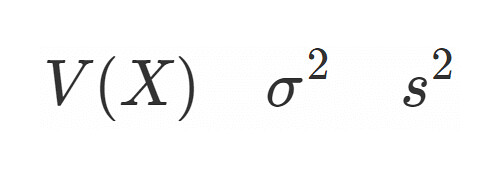
数学統計学分散

　今回も質問サイトで気になった質問です.

スポンサーリンク

分数とは
なぜ平均の差を2乗するのか
〆

分数とは

　 $n$ 個の実数データ $x=\{x_1,x_2,\dots ,x_n\}$ について, $x$ の平均を

$m :=: E(x) := \frac{1}{n}\sum_{k=1}^{n}x_k$

, そして分散を

$\sigma :=: V(x) := \frac{1}{n}\sum_{k=1}^n (x_k-m)^2$

, また標準偏差として

$\sigma := \sqrt{V(x)}$

と定義することはご存知の通りです.

　分散は簡単に言えば「データの散らばり具合」であり, もうちょっと具体的に言えば「各データが平均からどの程度離れているか」を与える統計指標の一つです.

　分散でデータを2乗してしまったため, 単位の次元をあわせるために標準偏差が存在します.

なぜ平均の差を2乗するのか

　「平均からの散らばり」であれば「各データと平均の絶対値の総和」でも良いはずです.

　つまり

$\nu = \frac{1}{n}\sum_{k=1}^n|x_k-m|\quad\dots(1)$

としても良いのではないか？という疑問です.

　因みに上記 $(1)$ は平均偏差という語で実際に統計指標として使われて「は」いるそうです.

　お察しの通り教科書でもまともに取り上げられないのが現実ですが.

　しかしこちらの方が各 $x_k-m$ を2乗して足し合わせるより計算も楽そうですね, なぜこちらより2乗偏差を使うのでしょうか.

微分できない場合がある

　直感的な視点では参考になりませんが, 概念・体系として扱う際に微分するシーンがあります.

　絶対値 $|x|$ は $x=0$ で微分不可能であるため, いずれ微分が関わる場合絶対値は「できるだけ使いたくない」のです.

場合分けをしなくて良い

　平均偏差では $n$ 個の絶対値が登場します.

　具体的な計算はもちろん, 変数のままで行う演繹において絶対値が登場するということは即ち場合分けを迫られるということです.

　絶対値の中身次第ですが, $n$ 個の絶対値がある場合最大で $n+1$ 通りの場合分けがあり得ます.

　 $n$ が多ければ多いほど, 全体の操作は困難になる恐れがあります.

　2乗してしまえば絶対値であっても $|x|^2=x^2$ と絶対値が外れるため, 場合分けをする必要がなくなる上上記の微分不可能性も解消されます.

　また有名な等式

$V(x)=E(x^2)-E(x)^2$

もシンプルに説明できます.

最小二乗の妥当性

　言うまでもなく, 絶対値を取る場合より二乗を取った方がその総和が大きくなるのはほぼ間違いないです.

　二乗したことによる平均からの「距離」が著しく大きくなることは尤もであるかどうかは議論の余地ある問題が出てきます.

　これは統計を取る上で大きく離れたデータの評価が目立った方が寧ろ望ましいでしょう, 特にデータが有限である場合は尚更, 分散は平均より遠いデータがより目立ち, 対して平均に近いデータは目立たない方がその意味をより増し得ます.

　また有限個の点を用いたフィッティング直線を求める最小二乗法は, 任意の点と求める直線のばらつきが最も小さくなる直線を求めるものであり, この構成は二乗偏差と似ています.

　平均偏差は誤差が正規分布に従う場合に限り良い評価を与えますが, 一般の場合は向かず, 寧ろ二乗偏差の方が向いており, これが前者が廃れた要因とも言われています.

〆

　というわけで, 絶対値を用いること自体は間違いではありませんが, 総合的な「使い勝手」を考えると二乗偏差に分がある…ということですね.