もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】分数(有理数)の間違った加法の定義考察

数学

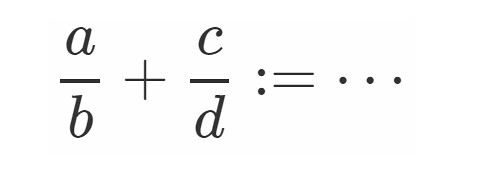
数学 分数 有理数 加法

　当然のように学ぶ分数・有理数の加法の定義ですが, なぜそれが正しいかを説明できるでしょうか？

 

 

スポンサーリンク

 

 

有理数の加法

　以下では基本的に有理数を扱います(分数でも構いませんが).

　有理数の加法の定義は, 知られている通り以下になりますね.

 

{ \displaystyle \frac{a}{b}+\frac{c}{d} := \frac{ad+bc}{bd} \\ \forall a,b,c,d\in\mathbb{Z},\, b,d\neq 0 }

 

　因みに乗法は

 

{ \displaystyle \frac{a}{b}\times\frac{c}{d} := \frac{ac}{bd} \\ \forall a,b,c,d\in\mathbb{Z},\, b,d\neq 0 }

 

ですね.

 

 

誤った定義

　しかし直観的に, 以下ではないのか…と考えたくなります.

 

{ \displaystyle \frac{a}{b}\dot{+}\frac{c}{d} := \frac{a+c}{b+d} \\ \forall a,b,c,d\in\mathbb{Z},\, b,d\neq 0 }

 

　一般の加法と区別するため, { \displaystyle + } の頭にドットを付けて { \displaystyle \dot{+} } としています.

　また更に言えば分母が { \displaystyle 0 } とする根拠も「この時点では」無いため, 削っておきましょう

 

{ \displaystyle \frac{a}{b}\dot{+}\frac{c}{d} := \frac{a+c}{b+d} \\ \forall a,b,c,d\in\mathbb{Z} }

 

　さて, この演算 { \displaystyle \dot{+} } は加法として正しいのでしょうか？

 

 

有理数に関わる諸定義

　今回は有理数ということで, 代数系で言うところの「体(=field)」に相当します.

　これを満たす条件は以下になります.

 

  1. 演算結果は(同値性を除いて)ただ一通りに定まる
  2. 結合律：
    { \displaystyle \left( \frac{a}{b}*\frac{c}{d} \right)*\frac{e}{f} = \frac{a}{b}*\left( \frac{c}{d}*\frac{e}{f} \right) }
  3. 単位元：
    　任意の { \displaystyle \frac{a}{b} } に対し, { \displaystyle \frac{a}{b}*\frac{m}{n}=\frac{m}{n}*\frac{a}{b}=\frac{a}{b} } を満たす元 { \displaystyle \frac{m}{n} } がただ一つ存在する
    (乗法単位元は0でないことが条件)
  4. 逆元：
    　任意の { \displaystyle \frac{a}{b} } に対して
    { \displaystyle \frac{a}{b}*\frac{a'}{b'} = \frac{a'}{b'}*\frac{a}{b} = \frac{m}{n} }
    を満たす元 { \displaystyle \frac{a'}{b'} } が, { \displaystyle \frac{a}{b} } に応じてただ一つ存在する
  5. 可換律：
    { \displaystyle \frac{a}{b}*\frac{c}{d}=\frac{c}{d}*\frac{a}{b} }
  6. 分配律：
    { \displaystyle \frac{a}{b}\left(\frac{c}{d}\dot{+}\frac{e}{f}\right) = \frac{a}{b}\frac{c}{d}\dot{+}\frac{a}{b}\frac{e}{f} }
    { \displaystyle \left(\frac{a}{b}\dot{+}\frac{c}{d}\right)\frac{e}{f} = \frac{a}{b}\frac{e}{f}\dot{+}\frac{c}{d}\frac{e}{f} }
  7. 正則性：任意の { \displaystyle \frac{a}{b}\neq 0 } が正則

 

　これらが一つでも成り立たなければ, 代数構造の理由で有理数と同じでないという事になります.

 

　因みに代数系とは, 代数学用語で「集合に演算構造を組み入れたモノ」を指します.

　集合はただ要素とその包含関係があるのみで, 演算や大小関係と言った概念は「まだ入っていない」状態です.

 

　一般にはそれらは当たり前にそれらが入っており, 使えて当たり前ですが, 集合とその代数系の本質に立ち入る代数学ではその「当たり前」は必ずしも通用しません.

　この考えは(数学における)位相も同じですね.

 

　では順番に確認してみましょう.

　因みに乗法は一般と同じであるとし, 先程は省略しましたが予め任意に { \displaystyle \frac{a}{b},\,\frac{c}{d},\,\frac{e}{f} } を取ります.

　かなりのボリュームです, 注意.

 

 

1.演算結果はただ一通りに定まる

　これは代数系の基本中の基本です.

　つまり一つの演算結果に対して, 「入力」はただ一通りという事です.

 

blog.thetheorier.com

　ちゃんと説明するならそれなりの文面を要します.

 

　ここで最も注目すべきは, 関数・写像における単射性でしょう, 簡単に言えば

 

{ \displaystyle f(a)=f(b)\Rightarrow a=b }

 

が成り立つことを言います.

 

　今回の { \displaystyle \dot{+} } は分母分子で独立しているため, 自然数がこれを満たしていることを以て成り立つことがわかります.

 

 

2.結合律

 

{ \displaystyle \left(\frac{a}{b}\dot{+}\frac{c}{d}\right)\dot{+}\frac{e}{f} }
{ \displaystyle = \frac{a+c}{b+d}\dot{+}\frac{e}{f} }
{ \displaystyle = \frac{a+c+e}{b+d+f} }

 

{ \displaystyle \frac{a}{b}\dot{+}\left(\frac{c}{d}\dot{+}\frac{e}{f}\right) }
{ \displaystyle = \frac{a}{b}\dot{+}\frac{c+e}{d+f} }
{ \displaystyle = \frac{a+c+e}{b+d+f} }

 

より成り立つことが分かります.

 

 

3.単位元

　まず加法について存在すると仮定し, { \displaystyle \frac{m}{n} } と置くと,

 

{ \displaystyle \frac{a}{b}\dot{+}\frac{m}{n} = \frac{m}{n}\dot{+}\frac{a}{b} = \frac{a}{b} }

 

, 整理して

 

{ \displaystyle \frac{a+m}{b+n} = \frac{m+a}{n+b} = \frac{a}{b} }

 

　これを満たす組 { \displaystyle (m,n) } はあるでしょうか？

 

　純粋に考えれば { \displaystyle (0,0) } しかありません, しかしこれは { \displaystyle \frac{0}{0} } であり, 一般には数ではありません.

 

　この時点でもう不穏な雰囲気ですが「順番の都合で」敢えて保留しましょう, つまり { \displaystyle (0,0)\equiv\frac{0}{0} } で良いとします.

　というのもこの時点ではまだ可逆であるかは分からないからです.

 

　なお乗法については通常のものとしたため省略します.

 

 

4.逆元

　まず加法について存在するとして { \displaystyle \frac{s}{t} } と置くと,

 

{ \displaystyle \frac{a}{b}\dot{+}\frac{s}{t} = \frac{s}{t}\dot{+}\frac{a}{b} = \frac{0}{0} }

 

, 整理すると

 

{ \displaystyle \frac{a+s}{b+t} = \frac{s+a}{t+b} = \frac{0}{0} }

 

ですね, つまり

 

{ \displaystyle s+a=0 ,\, t-b = 0 }

 

, よって

 

{ \displaystyle s=-a,\, t=-b }

 

を得ます.

 

　つまり { \displaystyle \frac{a}{b} } の逆元は存在するとして { \displaystyle \frac{-a}{-b} } ということになります.

 

　しかしこれは乗法の系に基づき { \displaystyle \frac{-a}{-b} = \frac{a}{b} } ですから, これから分かることは「{ \displaystyle \frac{a}{b} }の加法逆元は { \displaystyle \frac{a}{b} }」, つまり自分自身ということになります.

 

　なんとも違和感ある結果ですがこれも結果は兎も角得られましたから保留しましょう.

 

 

5.可換

　加法可換はとても簡単に導くことができます.

　通常の加法の可換性を利用して

 

{ \displaystyle \frac{a}{b}\dot{+}\frac{c}{d} }
{ \displaystyle = \frac{a+c}{b+d} }
{ \displaystyle = \frac{c+a}{d+b} }
{ \displaystyle = \frac{c}{d}\dot{+}\frac{a}{b} }

 

より成り立ちます.

 

　乗法可換については, やはり割愛します.

 

 

6.分配律

 

{ \displaystyle \frac{a}{b}\left(\frac{c}{d}\dot{+}\frac{e}{f}\right) }
{ \displaystyle = \frac{a}{b}\frac{c+e}{d+f} }
{ \displaystyle = \frac{ac+ae}{bd+bf} }

 

{ \displaystyle \frac{a}{b}\frac{c}{d}\dot{+}\frac{a}{b}\frac{e}{f} }
{ \displaystyle = \frac{ac}{bd}\dot{+}\frac{ae}{bf} }
{ \displaystyle = \frac{ac+ae}{bd+bf} }

 

となるためこちらも大丈夫です(もう一つは割愛).

 

 

7.任意のa≠0が正則

　「正則」という言葉は数学の色んな場面で使われ, かつカテゴリによって少しずつ意味が違います.

 

　今回の「正則」の意味は, 環, 簡単に言えば加減乗の可能な代数系 { \displaystyle R } であって, 単位元 { \displaystyle e\neq 0 } と { \displaystyle R } の元 { \displaystyle a } について

 

{ \displaystyle aa'=a'a=e }

 

を満たすような { \displaystyle R } の元 { \displaystyle a' } が存在することを言います.

　つまり逆元が存在することとほぼ同義で, このとき { \displaystyle a } は「正則である」, あるいは「可逆である」と言い, { \displaystyle a' } を可逆元と言います.

 

　逆元と同じとしか思えない定義ですが, 違いを挙げるならばこちらは「{ \displaystyle a\neq 0 }」と断っている点でしょうか.

 

　今回, 乗法は一般のそれとしたため乗法単位元は { \displaystyle 1\neq 0 } ですし, また

 

{ \displaystyle \frac{a}{b}\frac{s}{t}=\frac{s}{t}\frac{a}{b}=1=\frac{1}{1} }

 

を満たす組 { \displaystyle (s,t) } が { \displaystyle \frac{a}{b} } に応じて(同値性を除いて)ただ一つ存在することは直ちにわかります.

 

　従って正則性は問題ないことが分かります.

 

 

整理

　以上により, 成り立つか疑わしいモノとして

 

  • 4.(加法)単位元
  • 5.(加法)逆元

 

が挙げられます.

 

　仮に加法単位元を { \displaystyle \frac{0}{0} } と認めるとどうなるでしょう？

　加法逆元も問題ないように見えますが少し考えてみると少なくとも2点問題が生じます.

 

 

0/0は存在するのか

　今回の加法の定義を抜きにしても, 一般的に { \displaystyle \frac{0}{0} } という数は存在しません.

　簡単に理由を言えば「{ \displaystyle 0 } の乗法逆元が存在しないから」です.

 

　加法逆元が存在しないとなれば代数系で言う体, いや環, いやいや加法群はおろか群になりえないモノイドが精一杯です.

(群の世界では割り算を定義する遥か前の存在のため, { \displaystyle \frac{0}{0} }を認めることは強引ながら可能です. 困るのは「乗法逆元」です)

 

 

逆元が自分自身

　加法逆元で得た通り, 単位元の存在を前提として逆元が存在するならば, それは自分自身であると結論づけられます.

 

　減法は, 加法とその逆元を用いて

 

{ \displaystyle \frac{a}{b}\dot{-}\frac{c}{d}:= \frac{a}{b}\dot{+}\frac{c'}{d} }
({ \displaystyle \frac{c'}{d} } は { \displaystyle \frac{c}{d} } の加法逆元)

 

としたいものです, これは先程の「加法逆元が自分自身」から

 

{ \displaystyle \frac{a}{b}\dot{-} \frac{c}{d} = \frac{a}{b}\dot{+}\frac{a}{b} }

 

となります.

 

　この両辺に右から { \displaystyle \frac{c}{d} } を加えて整理すると, 単位元の定義より

 

{ \displaystyle \frac{a}{b}\dot{-}\frac{c}{d}\dot{+}\frac{c}{d}=\frac{a}{b}\dot{+}\frac{c}{d}\dot{+}\frac{c}{d} }
{ \displaystyle \Leftrightarrow\,\frac{a}{b}\dot{+}\frac{0}{0}=\frac{a}{b}\dot{+}\frac{2c}{2d} }
{ \displaystyle \Leftrightarrow\,\frac{a}{b}=\frac{a}{b}\dot{+}\frac{c}{d} }

 

　これが成立するのは { \displaystyle \frac{c}{d}=\frac{0}{0} } のみですね.

 

　例えば通常の有理数では当たり前の

 

{ \displaystyle 2-1=\frac{2}{1}-\frac{1}{1} = 1 }

 

を { \displaystyle \dot{+},\,\dot{-} } で計算すると,

 

{ \displaystyle \frac{2}{1}\dot{-}\frac{1}{1} }
{ \displaystyle = \frac{2}{1}\dot{+}\frac{1}{1} }
{ \displaystyle = \frac{2+1}{1+1} = \frac{3}{2} }

 

となってしまいます.

 

　逆元を用いる定義を無視して減法を定義しても, やはり不都合が生じてしまいます.

 

 

〆

　結果言えることは, { \displaystyle \frac{a}{b}\dot{+}\frac{c}{d}:=\frac{a+c}{b+d} } という定義は

 

  • 加法単位元および逆元が正しく定義できない
  • 上記により減法の自然な定義ができない

 

となります.

 

　興味ある方は, 逆に { \displaystyle \frac{a}{b}+\frac{c}{d}:=\frac{ad+bc}{bd} } の定義でなぜ大丈夫か, 確認してみましょう.

 

thetheorier