【数学】その定義は「正しいか」？

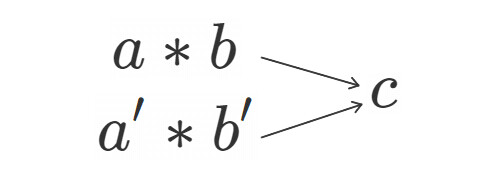
mathematics well-definded 数学うまく定義されている

　多くの方が聞き慣れない言葉だと思います.

その定義は「うまく定義されている」か？
- 「定義」が噛み合っていない例
  - 1.自然数と0
  - 2.素数の定義
- well-definded
〆

その定義は「うまく定義されている」か？

　定義とは言ってみれば諸々の議論に先立って決める概念や用語の名前や意味, 用法を明確にしたものを言います.

　言ってみれば「ルール」のようなものであり, 「そのように定義」すれば万人が共通の理解を得られるもので無ければなりません.

　肝心の定義なのに, 人によって解釈が異なる, 反論がある…では議論になりません.

　それゆえ, 議論に関わる総ての当事者が, 言語の差異こそあれその定義の意味がお互いに一致していることが大前提です.

　これは何も数学に限った事では無いでしょう.
　日常であれ会社であれ, ある事を話しているのにお互いにその言葉の意味を異にしているなら話は噛み合わず, 議論は進まないどころか最悪崩壊してしまいます.

「定義」が噛み合っていない例

1.自然数と0

　自然数は0を含むのか…というやり取りはとても多く見かけます.

　高校数学までは「含まない」で大方問題ありませんが, 大学数学になると公理で触れていない(どちらでも良い)こどあってか, 分野によっては含む方が都合が良いため「含む」場合もあります.

　この曖昧性のため, 場合によっては「ここでは自然数に0を含む」と断ったり, 誤解を与えるなら…ということで「正整数」と「非負整数」の二語を使うことで自然数という言葉を避けるなどの対応がなされることもあります.

2.素数の定義

　素数の定義として

「1と自分自身を約数に持たない自然数」

とする事が多いです.

　ここで問題になるのが「1は素数なのか」という問題です.

　上記のままでは(自然数の曖昧性はさておき)1も条件を満たしているため素数になることが出来ます.

　一般には, これを避けるために

1より大きい自然数
但し1は除く

のように断るでしょう.

　或いは素因数分解の一意性を以て除外するケースもありますが, (あくまでも主観ですが)これを持ち出すのは何だか循環論法に感じて僕は好きになれません.

　これらに囚われない定義として, 「真の約数」を用いた定義があります.

　つまり正整数aは1とa自身の2つ(a=1の場合は共通なので特別扱いされます)の正約数を必ずしも持つので, この2つを「真の約数」と呼びます.

　このとき

aが真の約数を持たない ⇔ aは素数
aが真の約数を持つ ⇔ aは合成数

として素数を定義します.

　この定義なら素因数分解の一意性は要請されませんし, また1は1自身以外に正約数を持たないので素数でない事がわかります.
　つまり素因数分解の一意性を使わずに1が素数でない事を説明出来ます.

　定義において「但し～とする」とすることはしばしばあるためそれ自体は悪いことではないこともまた事実です.

well-definded

　学生の立場であれば, この言葉が初めて登場し, 同時に頻繁に試行錯誤せねばならないのは同値関係絡みでしょう.

　このブログでも何度か登場しているこの概念は現代数学の画期的アイデアの一つであり, 同時に大学生を悩ませるものの一つでもあります.

blog.thetheorier.com

　商集合 $S\backslash\sim$ を商環たらしめるには然るべき加法と乗法を定義することになるわけですが, その際大抵は(大雑把ですが)

$[a]*[b] := [a*b]$

のように定義すれば事足りる事が多いでしょう(例外は幾らでもあるんですがイメージということで).
　因みに上の定義において, 左の $*$ は新しく定義した $S\backslash\sim$ 上での演算であり, 右辺のそれはS上での演算であることは言うまでもありません.

　問題はこれが定義として正しいか…という事です.
　これが晴れて正しいと分かれば, その定義はwell-defindedとなるわけです.

　例えば「曜日」で考えてみましょう, 曜日による法7の合同式を用いた剰余環は商環のとても分かりやすい例とした(多分)有名ですね.

　ある月の任意の「日付」は,

[日曜日], [月曜], [火曜], ..., [土曜]

という曜日による「類」のいづれか一つに必ず属します.

　よってこれらの7つの類を対象とした集合, 商集合に, 上で曖昧に書いたように, 自然な「加法」と「乗法」を定義できます.

　今回は加法について考えましょう.

　ある月の2日が日曜のとき, その月の11日は火曜ですね？

　もし2日の属する類[2]と11日の属する類を[11]と書き, これを用いて

[2]+[11] := [2+11]

, つまり「日曜」+「火曜」:=「2+11の属する曜日」と「定義」してみましょう.

2+11=13であり, 2日が日曜になる月の13日は木曜ですね.

　つまりこの定義では

「日曜」+「火曜」=「木曜」

となるはずです.

　これが正しいなら, 上で挙げた2日と11日以外の組み合わせでも同じ結果になってくれないと困ります.

　そこで例えば各々日曜と火曜に属する9日と18日でやってみるとどうなるか…と考えてみます.
　実際これは同じ結果を返す訳で, これが任意の組み合わせでも同じである事が確かめられる事で, 晴れてその「定義」は定義として正しい, well-defindedであるということになるわけです.

　即ち, $[a],[b]$ から任意の組み合わせ, 例えば $a,a'\in[a],\,b,b'\in[b]$ を取ってきても, $[a]*[b]$ と $[a']*[b']$ の結果が同じであるという保障は一般には無く, これが保障されて初めてwell-defindedと言えるわけです.

〆

　分数や有理数も同じです.

　例えば $\frac{1}{2}+\frac{1}{2}$ と $\frac{2}{4}+\frac{3}{6}$ がどちらも同じ値なのは, 分数(或いは有理数)の加法の定義

$\frac{a}{b}+\frac{c}{d} := \frac{ad+be}{bd}$

がwell-defindedであるからに他なりません.

もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.