もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】数学的帰納法の妥当性

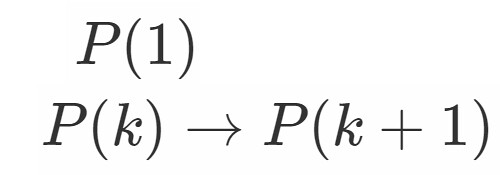
mathematical induction

　この問題は頻繁に取り上げられますね, 指摘される点は幾つかありますが一番は

 

{ \displaystyle n=k } で仮定して { \displaystyle n=k+1 } の場合を証明して何の意味があるのか

 

でしょうか.

 

スポンサーリンク

 

 

数学的帰納法とは

　その前に数学的帰納法を振り返りましょう.

 

[定義：数学的帰納法]

　主に任意の自然数 { \displaystyle n } に対する命題列 { \displaystyle P(n) } の証明法の一つであり, 一般に以下を証明するものである.

 

  • (1) { \displaystyle P(1) }
  • (2)任意の自然数 { \displaystyle k } について, { \displaystyle P(k)\Rightarrow P(k+1) }

 

　「主に～」としたのは, 一般的には { \displaystyle P(1) } から { \displaystyle P(n) } に対するものですが, ある { \displaystyle P(n) } から逆順に証明したり, 或いは { \displaystyle n } が整数であることもあるためです.

 

　構造としては, まず(1)によって { \displaystyle P(1) } が証明され, 続いて(2)によって個々の { \displaystyle k } について { \displaystyle P(k)\Rightarrow P(k+1) } が証明されているため, 例えば { \displaystyle P(2) } は

 

  • { \displaystyle P(1) } ...(1)より
  • { \displaystyle P(1)\Rightarrow P(2) } ...(2)より

 

という二つを仮定とした結論として演繹されます.

 

　{ \displaystyle P(3) } でも同じように

 

  • { \displaystyle P(1) }
  • { \displaystyle P(1)\Rightarrow P(2) }
  • { \displaystyle P(2)\Rightarrow P(3) }

 

の { \displaystyle 3 } つの仮定を用いて演繹されます.

 

　任意の { \displaystyle n } に対する { \displaystyle P(n) } であれば...もうお分かりですね？

 

 

誤解

　分かっている方には何の事もない話ですが, (2)に疑問を抱く原因は論理式で書けば一目瞭然です, 即ち

 

{ \displaystyle \forall k, \left[P(k)\Rightarrow P(k+1)\right] }

 

が正しい解釈です.

 

　誤解する方はこれをしばしば

 

{ \displaystyle \left\{ \forall k\left[P(k)\right] \right\} \Rightarrow P(k+1) }

 

と解釈してしまいます.

 

　ようは各々の { \displaystyle k } について { \displaystyle P(k)\Rightarrow P(k+1) } であることを証明しているのです.

 

　{ \displaystyle \forall k\left[P(k)\right] } はそもそも証明したいことそのものですから, そりゃあ「そんなもの証明して意味があるの？証明になるの？」となってしまいますね.

 

 

〆

　なお, 数学的帰納法は自然数を特徴づける性質の一つとなっています.

 

thetheorier