もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

素数の証明で使うMnは素数なのか

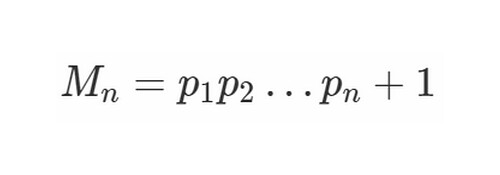
180729_01

　素数が無限に存在することの証明法で一番有名なのは背理法によるものでしょう.

　その際に使う「すべての素数の積に1を加えた数」への理解が一番のカギになります.

 

スポンサーリンク

 

 

Mnは素数？

　素数が無限個存在することを証明する方法として有名な手法は素数が { \displaystyle p_1, p_2,\dots , p_n } の有限個であると仮定し,

 

{ \displaystyle M_n := p_1\times p_2\times\dots\times p_n +1 }

 

なる数を扱うことになります.

 

　典型的な誤りは, この時点で

 

「{ \displaystyle M_n } は { \displaystyle p_1, p_2,\dots ,p_n } のいづれでも割り切れない, 従って { \displaystyle M_n } は { \displaystyle n } 個のいづれでもない素数であり, 仮定に反する」

 

と言ったものです.

 

　ぱっとみた感じ問題なく見えてしまいますね.

 

 

誤り

　なぜこれが誤りなのでしょう？

　それを考えるにはそもそも { \displaystyle M_n } が何であるかから考えることになります.

 

　そもそも { \displaystyle M_n } を定めた時点ではこれが素数であるかそうでないかは分かりません.

　{ \displaystyle M_n } が { \displaystyle n } 個のうちのどれかの素数なのか, そうでない合成数なのか, はたまた別なのかがこの時点では分からないからです.

 

　例えば

 

{ \displaystyle 2\times 3 +1=7 }

 

は素数ですが

 

{ \displaystyle 3\times 5 +1=16 }

 

は素数ではありませんね.

(あくまでも素数は有限個であると仮定しているのみであるため, { \displaystyle 2 } から順に並べる必要はありません, それが納得出来なければ例えば { \displaystyle 2\times 3\times 5\times 7\times 11\times 13 +1=30031 } が合成数となり { \displaystyle 59\times 509 } と因数分解できます)

 

　従って { \displaystyle M_n } は素数かそうでないかはこの時点ではわかりません, 故に素数であるとは決め付けられず場合分けが必要になります.

 

 

　もし { \displaystyle M_n } が素数ならば, 任意の { \displaystyle i(i=1,2,\dots ,n) } について { \displaystyle p_i\lt M_n } , つまり { \displaystyle p_i } よりも大きい素数の存在を認めることとなり, これは初めの仮定に反します.

 

 

　対して { \displaystyle M_n } が素数でない, つまり合成数である場合.

　この場合合成数なのですから { \displaystyle M_n } は一つの素数の累乗, もしくは2つ以上の異なる素数で割り切れるはずです.

　しかし { \displaystyle M_n } の定義から { \displaystyle M_n } はどの { \displaystyle p_i } でも割り切れません.

　初めの仮定よりこの { \displaystyle n } 個の素数がすべてですから合成数であることに矛盾します.

 

 

　結果 { \displaystyle M_n } が素数であると仮定しても合成数であると仮定してもどこかで矛盾を生じます.

 

　これは初めの仮定である「素数が有限個である」がそもそも誤りであるこということ, 然るに素数は有限でない, 無限個であることの証明となります.

 

　これが背理法と { \displaystyle M_n } を用いた正しい証明法です.

 

 

〆

　人によっては前者を省略してしまうため, このような誤解をしてしまう方が出てくるんじゃないかと思います.

　場合分けは必要だからやってる…ということですね.

 

thetheorier