もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】(-1)^nで遊ぼう

数学

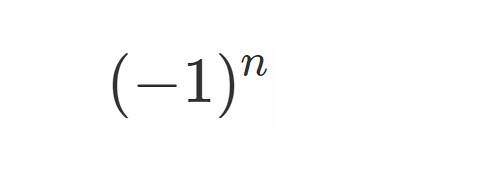
power of -1

　今回はちょっとした数学遊びです.

　質問サイトでごく稀に回答するときのアイデアとその応用です.

 

 

スポンサーリンク

 

 

(-1)^nを使った数列

　例えば以下の数列の一般項はどう表せるか考えてみましょう.

 

　{ \displaystyle \frac{1}{5},-1,\frac{1}{5},\,-1,\dots }

 

　少し間を置きます.

 

 

 

 

 

…

 

 

 

 

 

 

 

 

 

　色んなアイデアがあるでしょうが例えば以下はその解答の一つです.

 

{ \displaystyle a_n = \frac{1}{5}\frac{1-(-1)^n}{2} - \frac{1-(-1)^{n+1}}{2} }

 

　中には三角関数を駆使する方もおられます.

 

　ぱっと見難しいですが, 順を追っていけば対して難しくないことがわかります.

 

 

色々変形してみる

　単純な { \displaystyle (-1)^n } については以下であることがわかります( { \displaystyle n=8 } まで).

 

{ \displaystyle n}  { \displaystyle 1}  { \displaystyle 2}  { \displaystyle 3 }  { \displaystyle 4 }  { \displaystyle 5 }  { \displaystyle 6 }  { \displaystyle 7 }  { \displaystyle 8 } 
{ \displaystyle (-1)^n }  { \displaystyle -1 }  { \displaystyle 1 }  { \displaystyle -1 }  { \displaystyle 1 }  { \displaystyle -1 }  { \displaystyle 1 }  { \displaystyle -1 }  { \displaystyle 1 } 

 

　これを基本にもっと色々変形してみましょう.

 

 

{ \displaystyle n}  { \displaystyle 1}  { \displaystyle 2}  { \displaystyle 3 }  { \displaystyle 4 }  { \displaystyle 5 }  { \displaystyle 6 }  { \displaystyle 7 }  { \displaystyle 8 } 
{ \displaystyle (-1)^n }  { \displaystyle -1 }  { \displaystyle 1 }  { \displaystyle -1 }  { \displaystyle 1 }  { \displaystyle -1 }  { \displaystyle 1 }  { \displaystyle -1 }  { \displaystyle 1 } 
{ \displaystyle -(-1)^n }  { \displaystyle 1 }  { \displaystyle -1 }  { \displaystyle 1 }  { \displaystyle -1 }  { \displaystyle 1 }  { \displaystyle -1 }  { \displaystyle 1 }  { \displaystyle -1 } 
{ \displaystyle \frac{1+(-1)^n}{2} }  { \displaystyle 0 }  { \displaystyle 1 }  { \displaystyle 0 }  { \displaystyle 1 }  { \displaystyle 0 }  { \displaystyle 1 }  { \displaystyle 0 }  { \displaystyle 1 } 
{ \displaystyle \frac{1-(-1)^n}{2} }  { \displaystyle 1 }  { \displaystyle 0 }  { \displaystyle 1 }  { \displaystyle 0 }  { \displaystyle 1 }  { \displaystyle 0 }  { \displaystyle 1 }  { \displaystyle 0 } 

　{ \displaystyle 1 } から { \displaystyle (-1)^n } を足し引きして { \displaystyle 2 } で割ることで { \displaystyle 0 } と { \displaystyle 1 } を繰り返す数列が得られました.

 

　先程の数列 { \displaystyle a_n } はこの { \displaystyle \frac{1\pm(-1)^n}{2} } をうまく利用しているわけですね.

 

　これを応用すれば, 例えば { \displaystyle 1,0,2,0,3,0,4,0,\dots } となる数列の一般項 { \displaystyle b_n } は次のように表すことができます.

 

{ \displaystyle b_n = \frac{n+1}{2}\frac{1-(-1)^n}{2} }

 

 

 

複素数の利用

{ \displaystyle n}  { \displaystyle 1}  { \displaystyle 2}  { \displaystyle 3 }  { \displaystyle 4 }  { \displaystyle 5 }  { \displaystyle 6 }  { \displaystyle 7 }  { \displaystyle 8 } 
{ \displaystyle i^n }  { \displaystyle i }  { \displaystyle -1 }  { \displaystyle -i }  { \displaystyle 1 }  { \displaystyle i }  { \displaystyle -1 }  { \displaystyle -i }  { \displaystyle 1 } 
{ \displaystyle -i^n }  { \displaystyle -i }  { \displaystyle 1 }  { \displaystyle i }  { \displaystyle -1 }  { \displaystyle -i }  { \displaystyle 1 }  { \displaystyle i }  { \displaystyle -1 } 

　{ \displaystyle i } は複素単位です.

　このままでは虚数が点在します, これも工夫して実数のみにしてみましょう.

 

 

{ \displaystyle n}  { \displaystyle 1}  { \displaystyle 2}  { \displaystyle 3 }  { \displaystyle 4 }  { \displaystyle 5 }  { \displaystyle 6 }  { \displaystyle 7 }  { \displaystyle 8 } 
{ \displaystyle \frac{1+(-1)^n}{2}i^n }  { \displaystyle 0 }  { \displaystyle -1 }  { \displaystyle 0 }  { \displaystyle 1 }  { \displaystyle 0 }  { \displaystyle -1 }  { \displaystyle 0 }  { \displaystyle 1 } 
{ \displaystyle \frac{1-(-1)^n}{2}i^{n+1} }  { \displaystyle -1 }  { \displaystyle 0 }  { \displaystyle 1 }  { \displaystyle 0 }  { \displaystyle -1 }  { \displaystyle 0 }  { \displaystyle 1 }  { \displaystyle 0 } 

　交互に { \displaystyle 0 } と { \displaystyle 1 } を 繰り返し, 更に { \displaystyle 1 } は符号が入れ替わります.

 

 

　もっと複雑にするとどうでしょう.

 

 

{ \displaystyle n}  { \displaystyle 1}  { \displaystyle 2}  { \displaystyle 3 }  { \displaystyle 4 }  { \displaystyle 5 }  { \displaystyle 6 }  { \displaystyle 7 }  { \displaystyle 8 } 
{ \displaystyle (-1)^n-(1+(-1)^n)i^n }  { \displaystyle 0 }  { \displaystyle 1 }  { \displaystyle -2 }  { \displaystyle 1 }  { \displaystyle 0 }  { \displaystyle 1 }  { \displaystyle -2 }  { \displaystyle 1 } 
{ \displaystyle \frac{\frac{1-(-1)^n}{2}-(1-(-1)^ni^{n+1})}{2} }  { \displaystyle 0 }  { \displaystyle 0 }  { \displaystyle 1 }  { \displaystyle 0 }  { \displaystyle 0 }  { \displaystyle 0 }  { \displaystyle 1 }  { \displaystyle 0 } 

(スマホ縦向きだと長すぎて被ってると思います, すいません)

　{ \displaystyle \{0,1,-2,1\} }, または { \displaystyle \{0,0,1,0\} } で繰り返します.

 

 

3乗根の利用

　これまで使用した { \displaystyle (-1)^n } や { \displaystyle i } は原始2乗根または同4乗根に基づくため2項または4項周期が基本でした.

　では3乗根を用いるとどうでしょう, ここでは

 

{ \displaystyle x^2+x+1=0 }

 

の根の一つ, つまり { \displaystyle x^3=1 } の根のうち, { \displaystyle 1 } でないものの一方を { \displaystyle \omega } と置きます.

 

 

{ \displaystyle n}  { \displaystyle 1}  { \displaystyle 2}  { \displaystyle 3 }  { \displaystyle 4 }  { \displaystyle 5 }  { \displaystyle 6 }  { \displaystyle 7 }  { \displaystyle 8 } 
{ \displaystyle \omega^n }  { \displaystyle \omega }  { \displaystyle \omega^2 }  { \displaystyle 1 }  { \displaystyle \omega }  { \displaystyle \omega^2 }  { \displaystyle 1 }  { \displaystyle \omega }  { \displaystyle \omega^2 } 
{ \displaystyle \omega^{n+1} }  { \displaystyle \omega^2 }  { \displaystyle 1 }  { \displaystyle \omega }  { \displaystyle \omega^2 }  { \displaystyle 1 }  { \displaystyle \omega }  { \displaystyle \omega^2 }  { \displaystyle 1 } 
{ \displaystyle \omega^{2n+1} }  { \displaystyle 1 }  { \displaystyle \omega^2 }  { \displaystyle \omega }  { \displaystyle 1 }  { \displaystyle \omega^2 }  { \displaystyle \omega }  { \displaystyle 1 }  { \displaystyle \omega^2 } 
{ \displaystyle -(\omega^{n+1}+\omega^n) }  { \displaystyle 1 }  { \displaystyle \omega }  { \displaystyle \omega^2 }  { \displaystyle 1 }  { \displaystyle \omega }  { \displaystyle \omega^2 }  { \displaystyle 1 }  { \displaystyle \omega } 
{ \displaystyle \omega^{2n+1}-(\omega^n+\omega^{n+1}) }  { \displaystyle 2 }  { \displaystyle -1 }  { \displaystyle -1 }  { \displaystyle 2 }  { \displaystyle -1 }  { \displaystyle -1 }  { \displaystyle 2 }  { \displaystyle -1 } 
{ \displaystyle \frac{\omega^{2n+1}-(\omega^n+\omega^{n+1})+1}{3} }  { \displaystyle 1 }  { \displaystyle 0 }  { \displaystyle 0 }  { \displaystyle 1 }  { \displaystyle 0 }  { \displaystyle 0 }  { \displaystyle 1 }  { \displaystyle 0 } 

　{ \displaystyle \omega } の性質である

 

{ \displaystyle \omega^3=1 }
{ \displaystyle \omega^2+\omega+1=0 }

 

を上手に使います.

　これで { \displaystyle \{1,0,0\} } を周期とする数列の基礎が生成されました.

 

 

〆

　これらを利用することで, 規則的であるものの普通では解けないような数列の一般式を作ることができるかもしれません.

　上記はほんの一例です, 組み合わせ次第でもっと多様な基本列を作ることができます.

 

thetheorier