
2年以上前に似たような疑問を投げかけて放置したまま今に至りましたが, 解決しないまま新たなネタが持ち上がりました.
スポンサーリンク
これまで
原始根の定義そのものの話はもう割愛しましょう.
指数表は簡単に言えば対数表の整数バージョンのようなものです.
例えば素数7の原始根は3,5 の2つ, とりあえず今は3を例に挙げると
より, 素数7, 原始根3の指数表は以下となります.
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 2 | 1 | 4 | 5 | 3 |
前回はこれを単位円上にプロットすることで
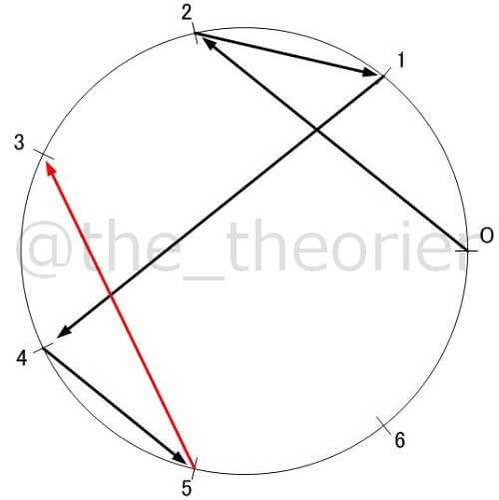
例えばこんな図形が得られました.
あるいは指数表の一部に巡回性が存在することを紹介しました.
今回は前者寄りです.
二次元平面にプロット
今回は得られた値を利用して平面に座標表示してみます.
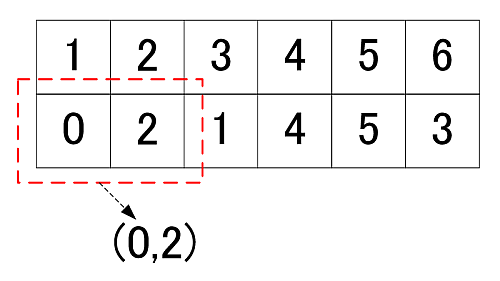
やることはさして難しくはありません.
表の隣り合う値同士を点とみなすだけです.
よって今回の, 素数7, 原始根3の場合
(0,2), (2,1), (1,4), (4,5), (5,3)
の5つの点を得ます.
これらを「表から生成した点」とでも呼ぶことにします.
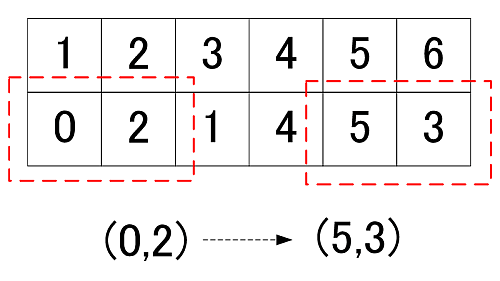
更に表から生成した点同士を, 得た順で両端から繋げていきます.
今回は (0,2)と(5,3), そして(2,1)と(4,5)を繋げます.
(1,4)は相方がいないのでプロットだけし, これを「孤立点」と呼ぶことにします.
指数表の項目数は必ず偶数であり, 素数3を除いて指数表には必ず孤立点が存在します.
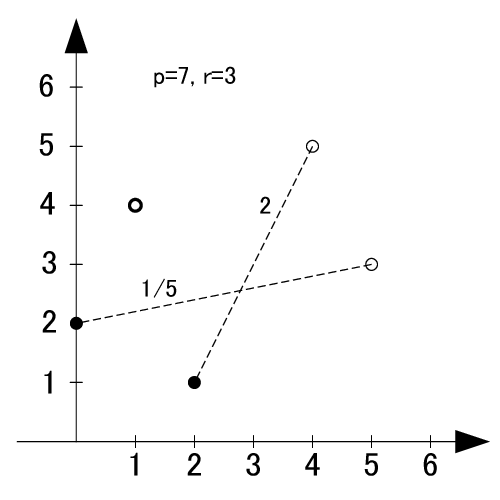
すると画像のようになります.
簡単に説明すると
- 塗りつぶしありの点 → 表の左側で生成した点
- 塗りつぶしなしの点 → 表の右側で生成した点
- 太字で塗りつぶしのない点 → 孤立点
, また生成点同士を繋げた線にある数字はその直線の傾きです.
意味があるかはまだわかりませんが塗りつぶしのある生成点を始点, 塗りつぶしなしの生成点を終点とみなした時になんらかの特徴を見いだせるかもしれません.
こうして見ると孤立点はともかくとして生成点による直線に線対称を見出すことができそうです.
では他の場合はどうでしょう?
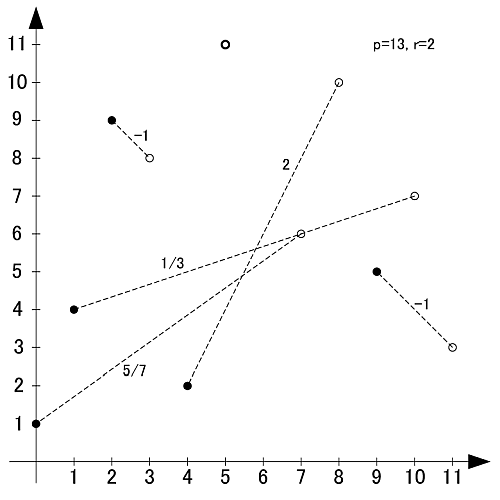
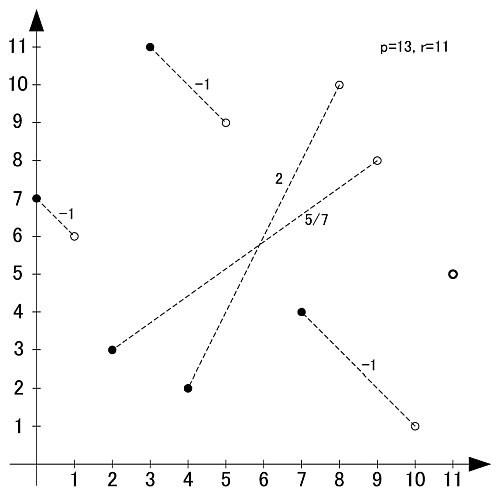
こちらは素数13, 原始根2の場合です.
先程見られた線対称性は見られず, 対して傾きが-1の直線が見られます.
実は素数7までの一部の指数表はその数が小さいのが原因で, この「傾き-1の直線」が最低でも1つ確認できます.
なお, 傾き-1の直線に該当しない各点のうち, x+y≦1, つまり「左下」のある点とそれx+y>1にある点に相似が見られるのでは…とも思ったのですが, この後で紹介しますが例えば素数17, 原始根14で例外があるためそんなに単純な話ではないようです.
ともかく説明はこれまでとして実際に見てもらう方が早いでしょう(というよりこれ以上よく分かっていません).
各素数・原始根ごとの図表
以下では素数p, 原始根rにおける, 上記で説明した通りにプロットした図表を紹介します.
手間の都合で素数19までとなっています.
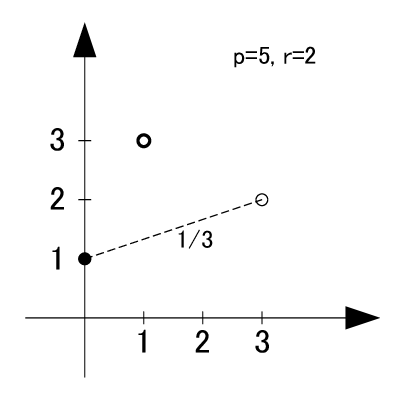
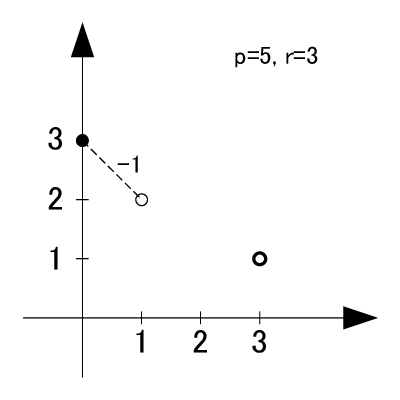
p=5
素数5の原始根は2,3の2個です.
p=7
素数7の原始根は3,5の2個です.
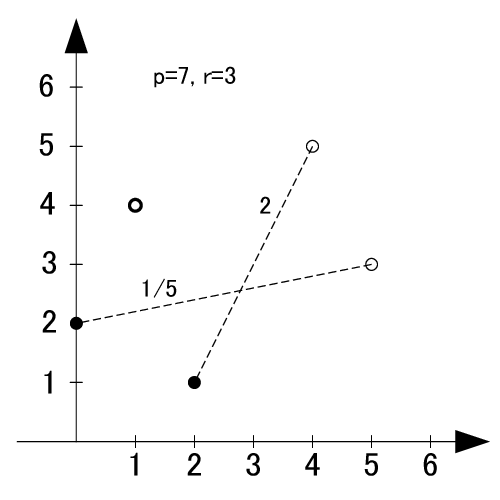
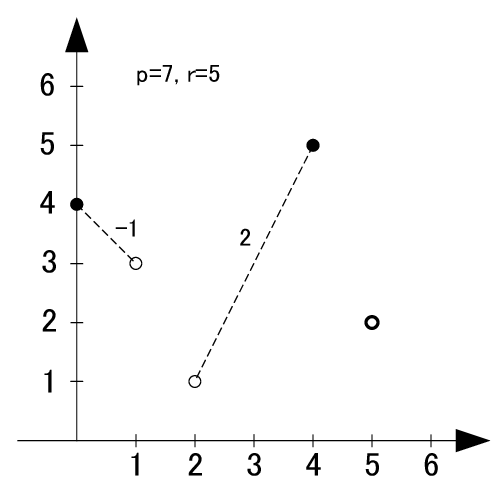
p=11
素数11の原始根は2,6,7,8の4個です.
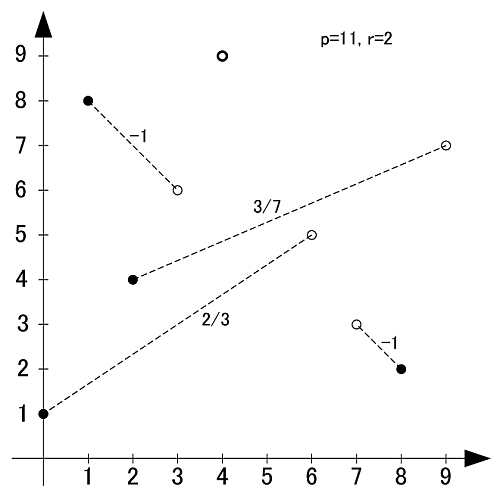
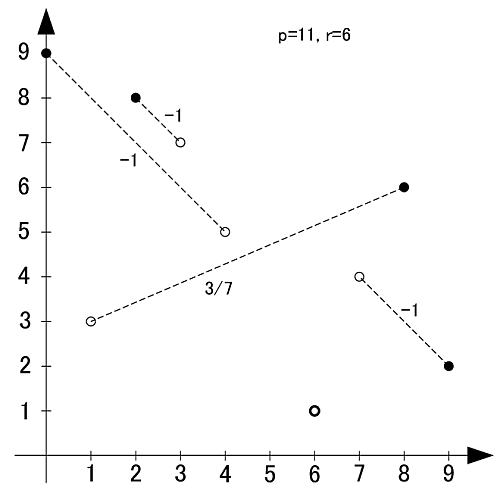
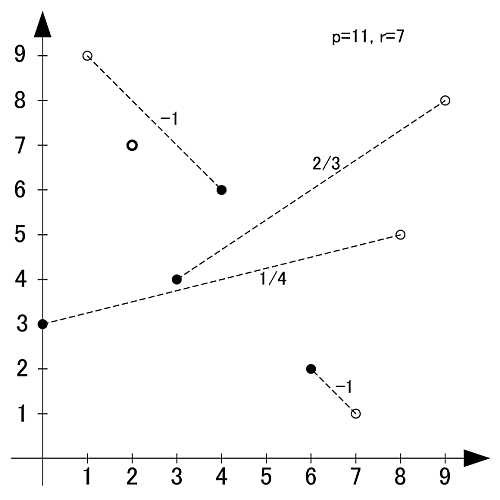
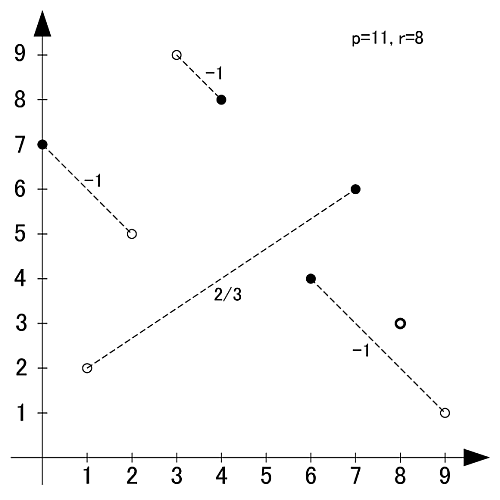
p=13
素数13の原始根は2,6,7,11の4個です.
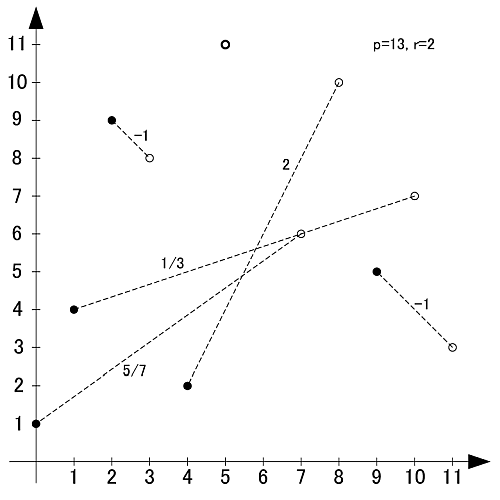
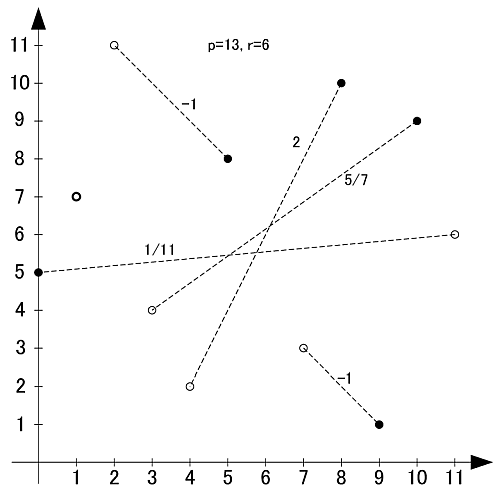
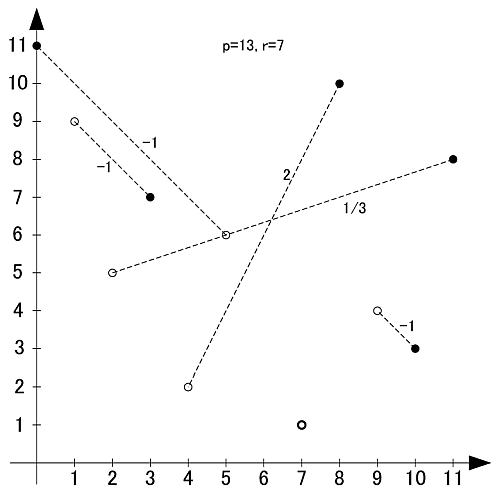
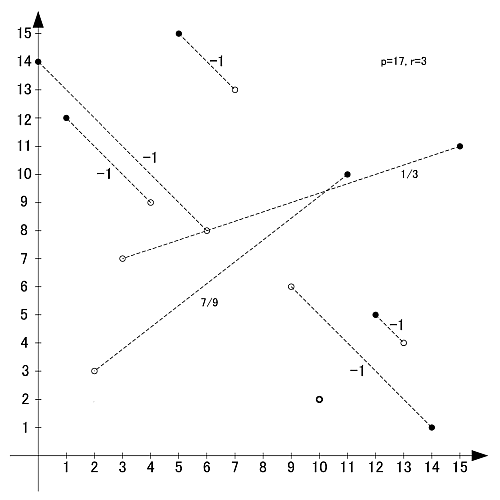
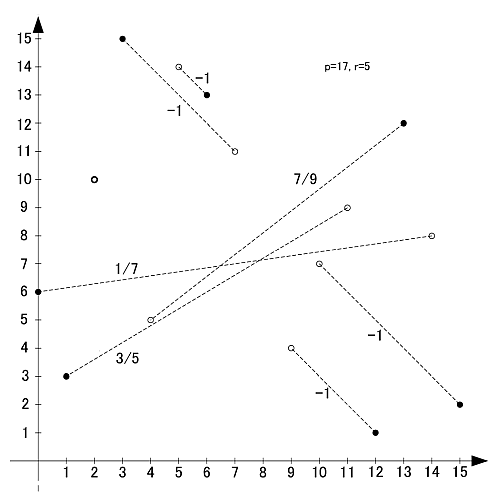
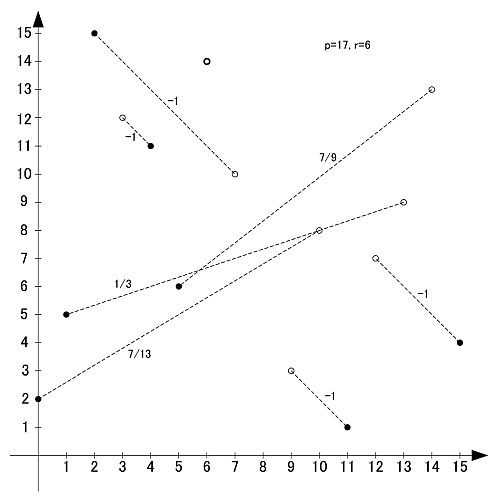
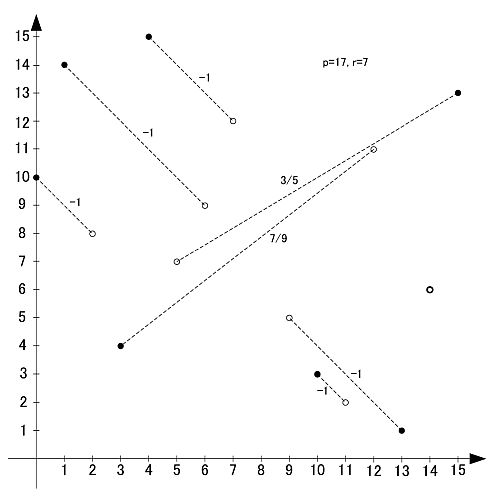
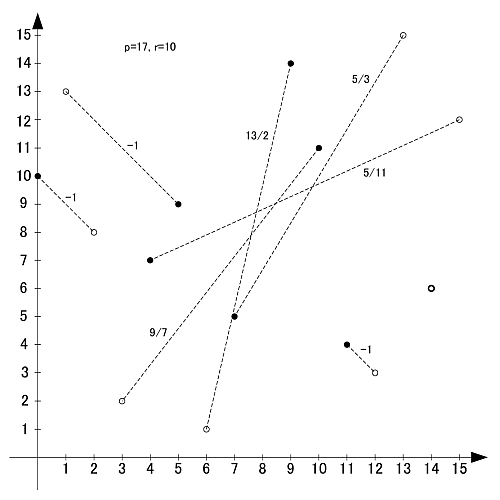
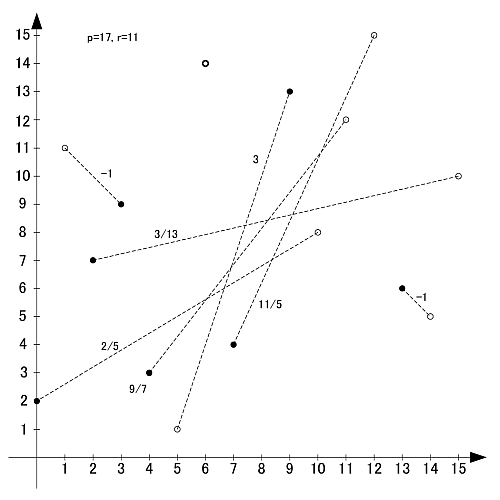
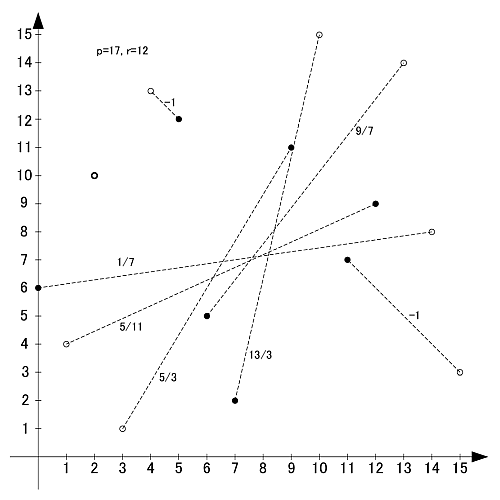
p=17
素数17の原始根は3,5,6,7,10,11,12,14の8個です.
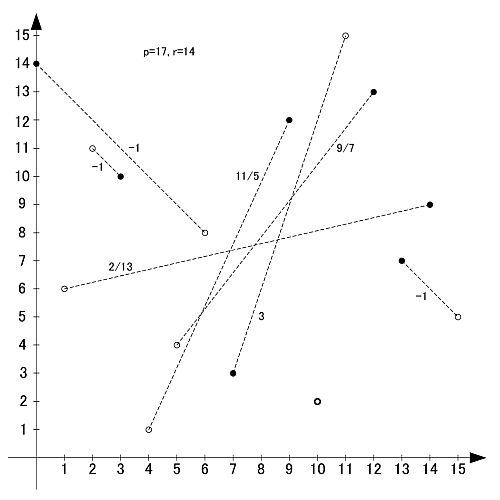
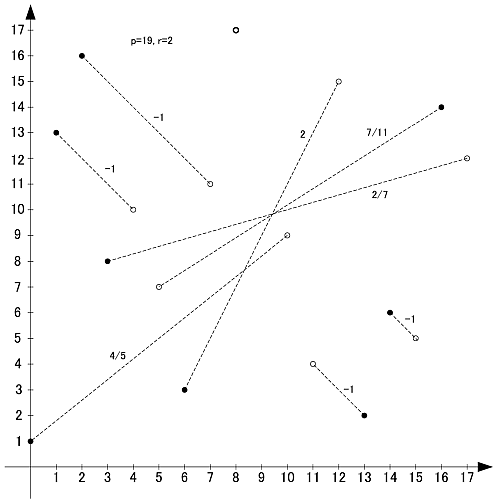
p=19
素数19の原始根は2,3,10,13,14,15の6個です
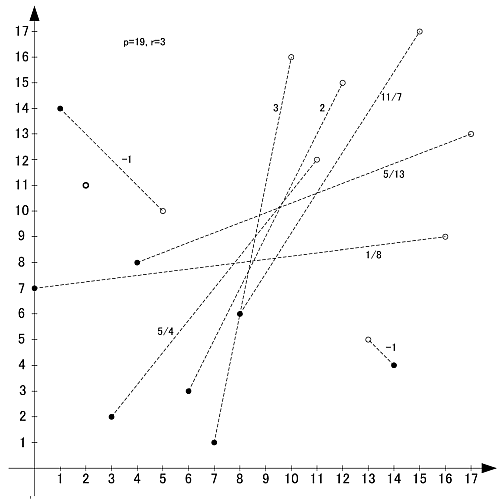
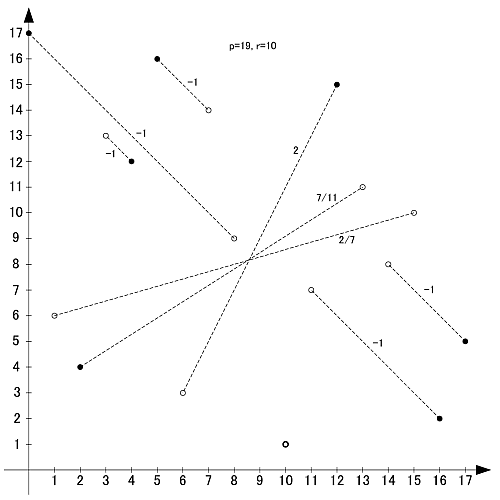
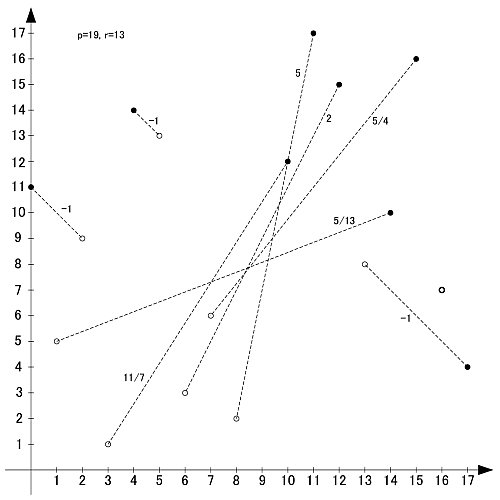
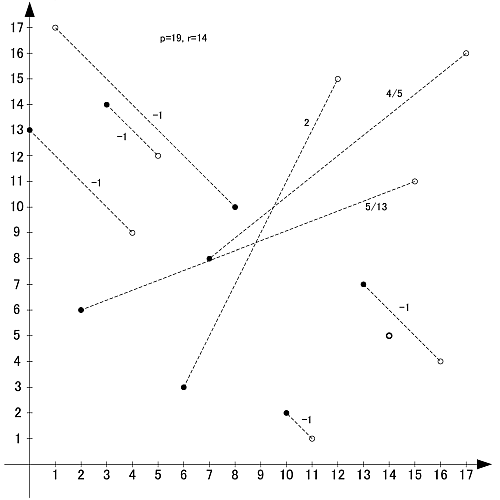
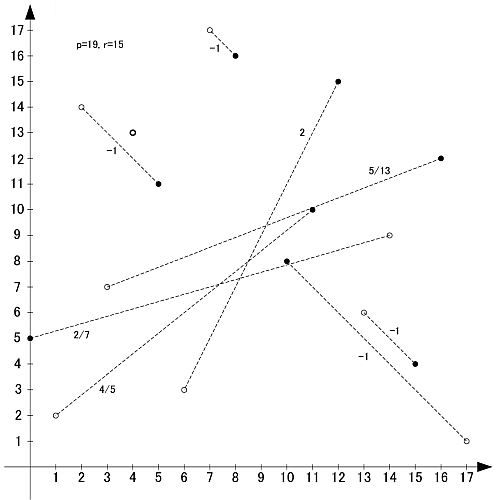
〆
同じ素数同士で互いに線対称や点対称などの関係にあるものがありそうでない, 傾き-1の直線の数も素数と原始根の組と関係があるのかどうか, -1以外の直線はなぜすべて正になるのか, その傾きの値も似たものばかり…
色々と分からないことが多いですね, これまでのと組み合わせて指数表を正攻法で解く以外のヒントになればと色々試しているのですが…
