もう一人のY君

主にiPhoneのショートカットアプリのレシピやTipsなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】背理法を用いた無理数の証明で既約分数を使う理由

数学

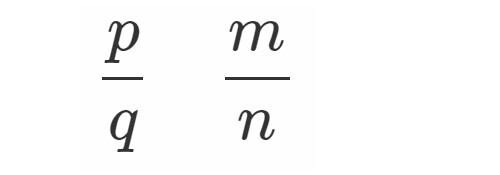
170221_12

　先日, このような質問がありました.

 

　{ \displaystyle \sqrt2 } が無理数であることの背理法を用いた証明で, なぜ有理数でなく既約分数と仮定するのか

 

　意訳してしまえば, 「既約分数でない有理数を抜きにして既約分数だけ証明してそれが本来の証明になっているのか？」ということです.

 

 

「一般性を失わない」

　結論から言えば, 今回の場合は既約分数だけ考えても一般性を失いません.

　「一般性を失わない」という用語が何なのかは以下の説明で分かることでしょう.

 

　さて本題ですが, 既約分数だけで本当に大丈夫なのか？ということなので敢えて既約でないことを想定して次のように有理数 { \displaystyle \frac{a}{b} } と既約分数 { \displaystyle \frac{a'}{b'} } を用意します.

 

{ \displaystyle \frac{a}{b} = \frac{a'k}{b'k} }

{ \displaystyle k } は { \displaystyle 0 } でない任意の整数

 

　即ち, { \displaystyle \frac{a}{b} } は既約分数でない有理数です.

 

　先程の引用と同じ, 「{ \displaystyle \sqrt2 } が無理数である」ことの証明で例としましょう.

　背理法ですから有理数であると仮定し, { \displaystyle \sqrt2 = \frac{a}{b} } とします.

　これを変形して

 

{ \displaystyle \sqrt2b = a \\ \Rightarrow 2b^2 = a^2 \\ \Leftrightarrow 2(b'k)^2=(a'k)^2 \\ \Leftrightarrow 2b'^2 = a'^2 }

 

…となります.

 

　最後の等式は, はじめに既約分数と仮定した場合に同じやり方をした場合と同じ結論ですね.

 

　つまり有理数と仮定してアプローチしても, 既約分数としてアプローチしても, 結果は後者と同じになるわけです.

 

 

既約分数は有理数を代表する

　はじめに置いたように, 任意の有理数 { \displaystyle \frac{a}{b} } は, 対応する { \displaystyle 0 } でない整数 { \displaystyle k } と既約分数 { \displaystyle \frac{a'}{b'} } を用いて

 

{ \displaystyle \frac{a}{b} = \frac{a'k}{b'k} }

 

を満たします.

　厳密に言えば { \displaystyle k } は { \displaystyle a, b } の最大公約数となります.

 

　任意の有理数は, 自分自身が既約であるか, そうでない( { \displaystyle a, b } の最大公約数 { \displaystyle \text{gcd}(a, b) } が { \displaystyle 1 } より大きい)ならば, 分母分子を { \displaystyle \text{gcd}(a, b) } で割ったものが既約分数となります.

 

　つまり任意の有理数は, 必ずいづれかの既約分数に対応します.

　

　従って何かを論ずる際, 例えばそれを有理数とするところを既約分数に制限しても問題ないときがあります, これが「一般性を失わない」の一つです.

　高校まででは余り使いませんが, 数学ではよく使う用語です.

 

 

〆

　因みに今回のようなケースは有名なので「既約分数としても一般性を失わない」なんていちいち書きません.

　分かってる人にとっては当たり前でも, 学んだばかりであったりまだきちんと理解していない内は混乱しますよね.

 

　この用語をまともに使うようになるのは大学数学になってからでしょう.

 

 

blog.thetheorier.com

　念のためですが有理数は「分数で表せる数」ではありませんよ.

 

 

thetheorier