もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU

【数学】(-1)^nで遊ぼう(原始n乗根編)

数学

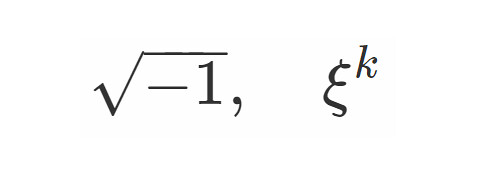
√-1で遊ぼう 1の原始n乗根

　先日紹介した, 0と1とを繰り返す数列を生成するロジックを, { \displaystyle \sqrt{-1} } から見出しました.

 

 

スポンサーリンク

 

 

前回

blog.thetheorier.com

　前回は { \displaystyle \sqrt{-1} } をはじめ複素単位である { \displaystyle i }, そして1の3乗根である { \displaystyle \omega } を利用しました.

　後半はその場の思いつき感丸出しでちょっとエレガントでなかったのですが, もう少し考えてみたところ, 1の原始n乗根に気づきました.

 

 

1のn乗根, 1の原始n乗根

　1のn乗根, 及び原始n乗根とは, いづれも方程式

 

{ \displaystyle x^n=1 }

 

の解であることですが, 後者は { \displaystyle 1 } を除きます.

　言い換えると { \displaystyle 1 } の原始 { \displaystyle n } 乗根とは,

 

{ \displaystyle n } 乗してはじめて { \displaystyle 1 } となる複素数

 

を指します.

 

　これらはド・モアブルの定理によって以下で表現できます.

 

{ \displaystyle x=\cos\frac{2\pi k}{n}+i\sin\frac{2\pi k}{n},\ }{(k=0,1,\dots ,n-1) }

 

　また { \displaystyle 1 } の原始 { \displaystyle n } 乗根の一つを { \displaystyle \xi } とすると, 任意の自然数 { \displaystyle k } について

 

{ \displaystyle \left(\xi^k\right)^n \\ =\xi^{kn} \\ =\xi^{nk} \\ = \left(\xi^n\right)^k \\ =1^k \\ =1 }

 

ですから, { \displaystyle \xi^k } もまた { \displaystyle 1 } の { \displaystyle n } 乗根であることがわかります(原始 { \displaystyle n } 乗根であるとは限りません).

　{ \displaystyle 1 } の原始 { \displaystyle n } 乗根は位数 { \displaystyle n } の巡回群であり,

 

{ \displaystyle \xi, \xi^2, \xi^3,\dots ,\xi^{n-1},\xi^n(=1) }

 

は互いに異なる複素数です.

 

　この { \displaystyle n } 個の複素数はいづれも { \displaystyle x^n=1 } の解ですから

 

{ \displaystyle (x-\xi)(x-\xi^2)\dots (x-\xi^n)=0 }

 

を満たしており, 左辺を展開して { \displaystyle x^{n-1} } の係数を比較すれば

 

{ \displaystyle \xi+\xi^2+\dots +\xi^{n-1}+\xi^n=0 }

 

を得ます.

　この事実が今回の肝となります.

 

 

本題

　では本題に入りましょう, 数列の添字を { \displaystyle n } とすると原始 { \displaystyle n } 乗根の { \displaystyle n } と被ってしまうため { \displaystyle a_m } と { \displaystyle m } を使うことにします.

 

({ \displaystyle n\nmid m }のとき)

{ \displaystyle \xi^{km}≠1,\, (k=1,2,\dots ,n-1) \\ \xi^{nm}=1 }

 

より,

 

{ \displaystyle \xi^m +\xi^{2m}+\dots +\xi^{(n-1)m}+\xi^{nm}=0 }

 

　後のために { \displaystyle \rho_{(m,n)} }{ \displaystyle :=\xi^m +\xi^{2m}+\dots +\xi^{(n-1)m}+\xi^{nm} } と置きます.

 

 

({ \displaystyle n\mid m }のとき)

　任意の { \displaystyle m } について { \displaystyle \xi^{km}=1,\, (k=1,2,\dots ,\, n) } より,

 

{ \displaystyle \rho_{(m,n)} \\ =\xi^m +\xi^{2m}+\dots +\xi^{(n-1)m}+\xi^{nm} \\ =1+1+\dots +1 \\ =n }

 

となります.{ \displaystyle \quad\square }

 

 

整理

　よって, この { \displaystyle \rho_{(m,n)} } は「初項から { \displaystyle m-1 } 項目までが { \displaystyle 0 } , { \displaystyle m } 項目が { \displaystyle n } 」で以降同じように繰り返す数列と言えます.

 

　使い勝手のために各項を { \displaystyle n } で割った { \displaystyle \frac{\rho_{(m,n)}}{n} } を使えば良いでしょう.

 

　また「1」の箇所をずらしたい, 例えば初項を { \displaystyle 1 } としたい場合は例えば

 

{ \displaystyle \frac{\rho_{(m,m+n-1)}}{n} }

 

とすれば良い事が分かります.

 

　因みに { \displaystyle \sqrt{-1} } は { \displaystyle n=2 }, { \displaystyle i } は { \displaystyle n=4 }, { \displaystyle \omega } が { \displaystyle n=3 } の場合であることもすぐ分かると思います.

 

 

具体例

　例えば, { \displaystyle a,b,c,d,a,b,c,d,\dots } と繰り返す数列の一般項 { \displaystyle a_m } は, この { \displaystyle \rho_{(m,n)} } を用いることで

 

{ \displaystyle a_m }{ \displaystyle = \frac{a\rho_{(m,m+3)}+b\rho_{(m,m+2)}+c\rho_{(m,m+1)}+d\rho_{(m,m)}}{4} }

 

となります.

 

 

〆

　前回もひょんな思いつきでしたが, 今回も「そういえば原始 { \displaystyle n } 乗根なんてあったな…」という程度で思いついた…というより「思い出した」ですね.

 

　質問サイトなんかでよくある(?)ヒントの緩い数列の特定項を当てる問題なんかで使えます(狭いですねw).

 

　これで多少無茶振りな数列の問題も解決できます(誰得).

 

thetheorier