もう一人のY君

主にiPhoneのショートカットアプリのレシピやTipsなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

(数学)指数表に幾何学的特徴を見る

数学

160827_00

　先日, 原始根や指数を紹介したのは, 今回の記事を紹介するためでした

　やっと書ける…

 

[Contents]
 

 

原始根・指数についておさらい

thetheorier.hatenablog.com

　前回, 原始根と指数について触れましたが, 改めて多さっぱに書いておきます.

 

[定義：原始根]

　素数 { \displaystyle p } と, { \displaystyle p } で割り切れない整数 { \displaystyle a } について, { \displaystyle a } が { \displaystyle p-1 } に対応するとき, つまり { \displaystyle p-1 } よりも小さな正指数で { \displaystyle a^{e}\equiv 1\pmod p } という形にならないとき, { \displaystyle a } は { \displaystyle p } の原始根と言います.

 

 

[定義：指数]

　素数 { \displaystyle p } とその任意の原始根 { \displaystyle r }, また { \displaystyle a\not\equiv 0\pmod p } なる任意の整数について

{ \displaystyle r^{\alpha}\equiv a\pmod p }

を満たすような指数 { \displaystyle \alpha } が, { \displaystyle a } に応じて { \displaystyle 0\leq \alpha\lt p-1 } の範囲にただ一つ存在します.

　この { \displaystyle \alpha } を, { \displaystyle r } を底とする { \displaystyle a } の指数と言い, { \displaystyle \text{Ind}_{r}(a) } と書き表します. 

 

　先日も述べたように, 原始根は対数の底, 指数は対数そのものと似ています.

 

　また

 

{ \displaystyle 1, r, r^{2}, \dots, r^{p-2} }

 

が規約代表であることから, これらによる指数は互いに1対1となり, これを用いた指数表を作ることができます.

 

　前回, { \displaystyle p=7, r=3 } の場合では

 

{ \displaystyle 3^{0}=1\equiv 1\pmod 7 }

{ \displaystyle 3^{1}=3\equiv 3\pmod 7 }

{ \displaystyle 3^{2}=9\equiv 2\pmod 7 }

{ \displaystyle 3^{3}=2\times 3\equiv 6\pmod 7 }

{ \displaystyle 3^{4}\equiv 6\times 3\equiv 18\equiv 4\pmod 7 }

{ \displaystyle 3^{5}\equiv 4\times 3\equiv 12\equiv 5\pmod 7 }

 

であることから, 以下のような指数表ができることを紹介しました.

 

{ \displaystyle p=7, r=3 } の指数表
{ \displaystyle N } 1 2 3 4 5 6
{ \displaystyle \text{Ind}_3(N) } 0 2 1 4 5 3

 

　今回はこの表を図形に表してみたいと思います.

 

 

指数表を図形にしてみる

　色んな表現方法はあると思いますが, 今回は単位円を { \displaystyle p } 分割して番号を振り, { \displaystyle \text{Ind}_{r}(a) } の値に沿って矢印線を引いていきます.

　まぁ文章で書くより実際に図を見てもらった方が早いですね.

　上の { \displaystyle p=7, r=3 } を例にしてみましょう.

 

 

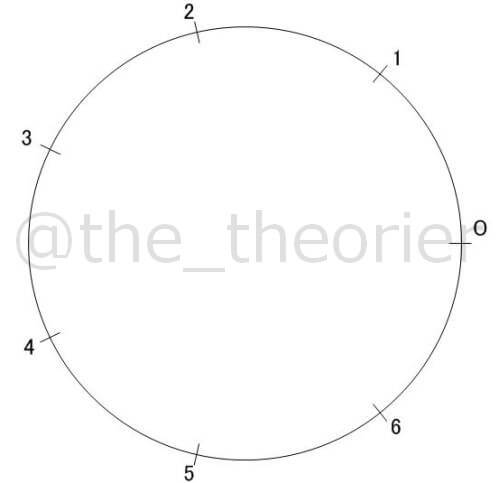
160827_01　 

　まず円を描き, 円周を7等分して番号を付けます.

　付け方は色々あるでしょうがここでは右端を0として反時計回りにつけていきます.

 

 

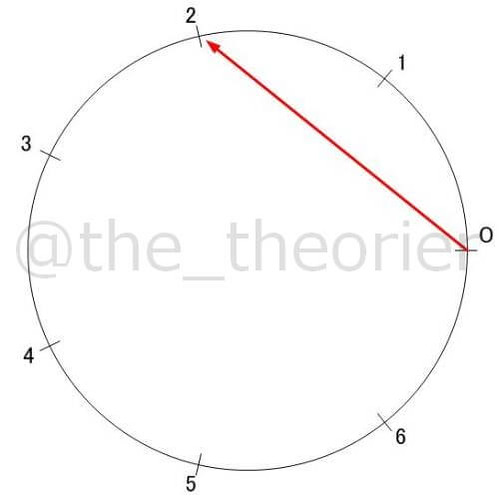
160827_02

　決まりに従って矢印を描いていきます.

　{ \displaystyle \text{Ind}_{3}(1)=0, \text{Ind}_{3}(2)=2 } なのでまず 0 から 2へ矢印を引きます.

 

 

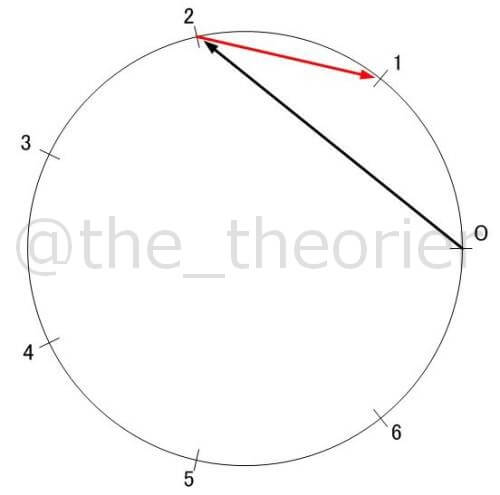
160827_03

　続いて { \displaystyle \text{Ind}_{3}(2)=2, \text{Ind}_{3}(3)=1 } なので 2 から 1 へ引きます.

 

 

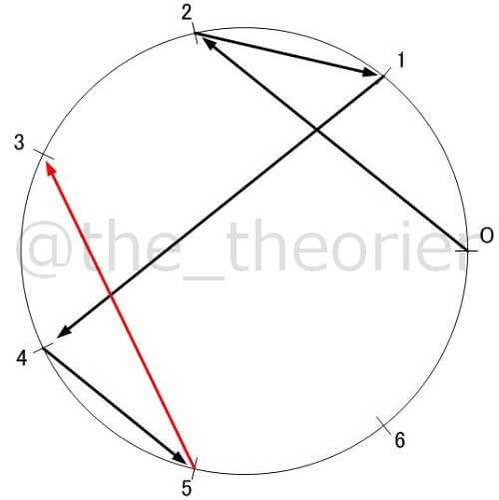
160827_06

　この調子で描いていくと上のようになります.

　本数が少ない上, まだ一つしか描いてないので特徴を評価することはできそうにありません.

 

 

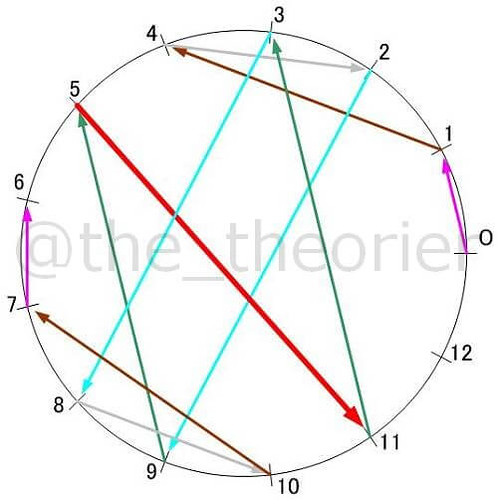
160827_06a

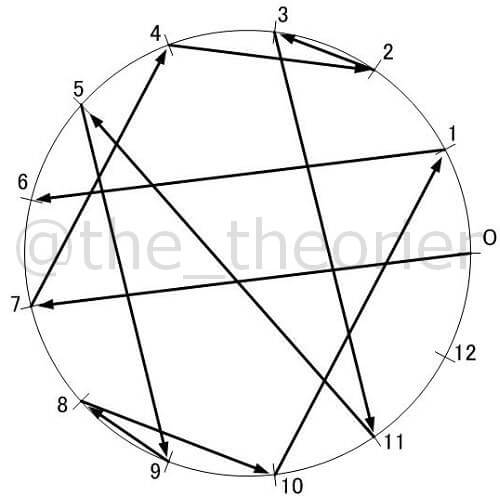
　ではこちらはどうでしょう, { \displaystyle p=13, r=2 } の場合です.

　既に色を付けたので分かるでしょうが, 5 から 11の矢印(以下5→11と書きます)を除き, すべての矢印が, 線対象となる矢印の組を持っていることが分かります.

　具体的には0→1と7→6, 1→4と10→7, 4→2と8→10, そして2→9と8→3がそれぞれ似た特徴を持っています.

　また孤立した5→11は指数表の丁度真ん中となっています(下記数表を参照).

　矢印も, この孤立した矢印を境に, 前半と後半がちょうど逆転した関係となっていることが観察されます.

　最後に他の例も挙げますが, 上の特徴は如何なる素数と原始根の組であっても見られるものと思われます.

　何か法則が見出せそうですね.

 

 

原始根が異なるとどう変わるか

　例えば { \displaystyle p=13 } は, { \displaystyle r=2 } 以外にも原始根を持っています.

　各々について同じように描いてみると下のようになりました.

 

 

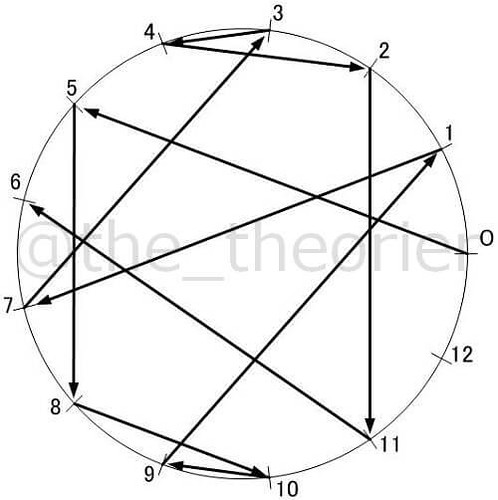
160827_07_13-6

　{ \displaystyle p=13, r=6 }

 

 

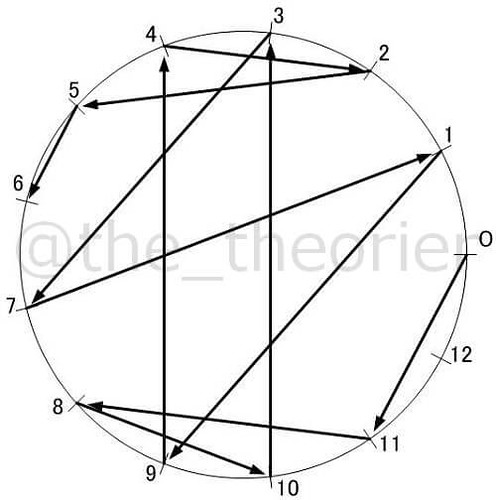
160827_07_13-7

　{ \displaystyle p=13, r=7 }

 

 

160827_07_13-11

　{ \displaystyle p=13, r=11 }

 

　同じ素数 { \displaystyle 13 } でも, 原始根によって少しずつ姿が違いますね.

 

 

図形化したことで推測されること

　いくつかのパターンから類推するに, 以下の等式が成り立つであろうと考えられます.

 

 

[推論]

　素数 { \displaystyle p } とその原始根 { \displaystyle r } について,

{ \displaystyle \Bigl|\text{Ind}_{r}\frac{p-1}{2} - \text{Ind}_{r}\frac{p+1}{2}\Bigr| = \frac{p-1}{2} }

 

　まだ証明に至ってはいませんが, これが意味する所は { \displaystyle N=1, 2, \dots \frac{p-1}{2} } までの指数表が分かっていれば, この推論を用いて後半の指数が導かれるということです.

　実際にはそれほどメリットがあるわけでもないんですけどね.

 

 

〆

　二項係数剰余を考えてるうちに何故か思いついた発想ですが, 世間に知られたものであるかは知りません.

 

　以下に { \displaystyle p=5 } から { \displaystyle 29 } までの素数の, 正値最小原始根での図を紹介します.

　( { \displaystyle p=3 } については今回のような描画ができないため, 除外します )

 

 

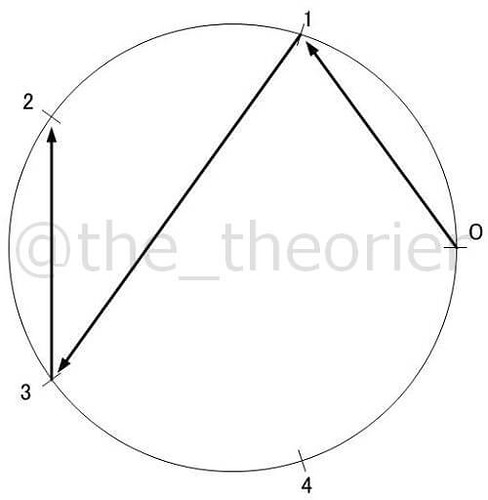
160827_07_5-2

　{ \displaystyle p=5, r=2 }

 

 

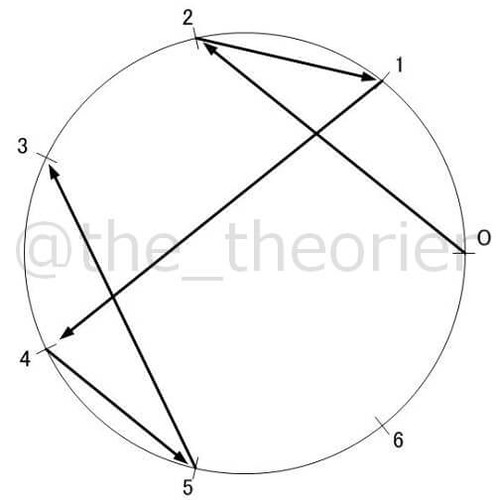
160827_07_7-3

　{ \displaystyle p=7, r=3 }

 

 

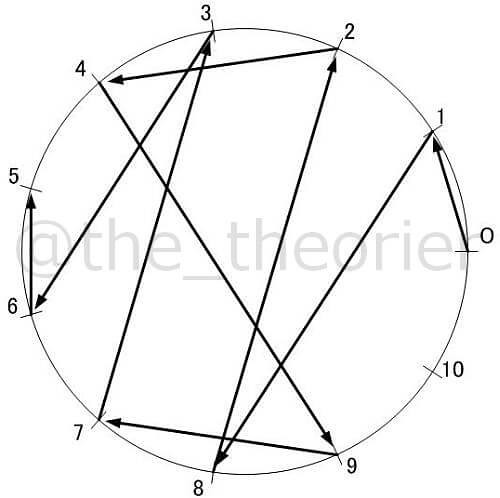
160827_07_11-2

　{ \displaystyle p=11, r=2 }

 

 

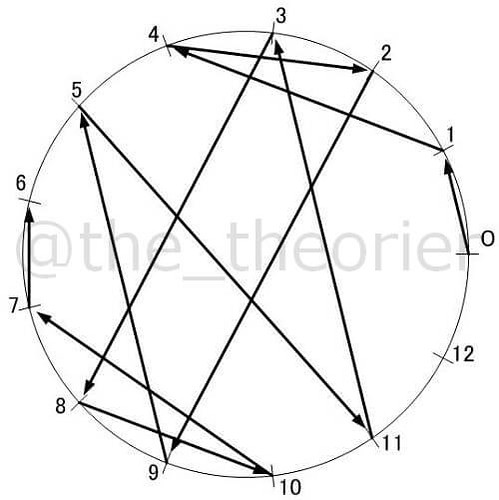
160827_07_13-2

　{ \displaystyle p=13, r=2 }

 

 

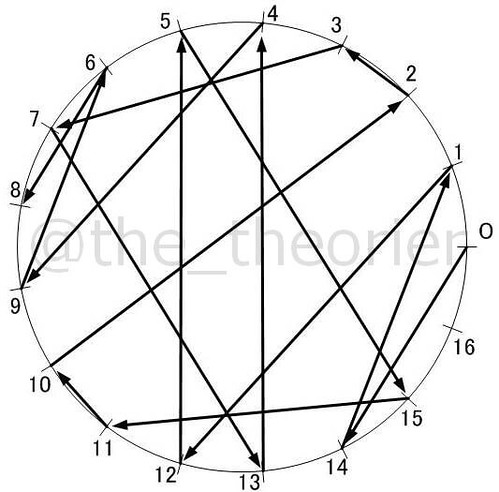
160827_07_17-3

　{ \displaystyle p=17, r=3 }

 

 

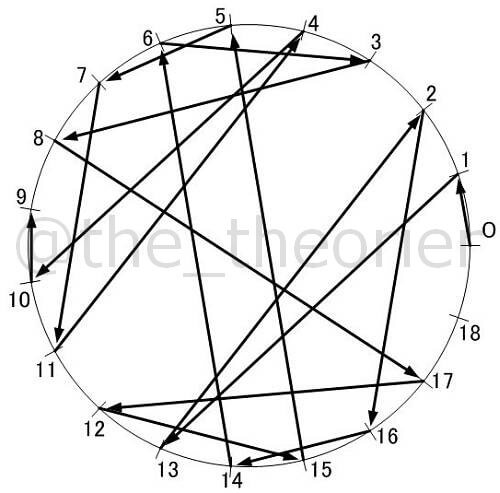
160827_07_19-2

　{ \displaystyle p=19, r=2 }

 

 

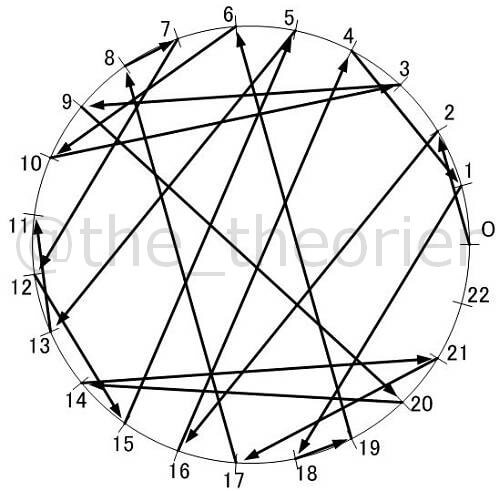
160827_07_23-5

　{ \displaystyle p=23, r=5 }

 

 

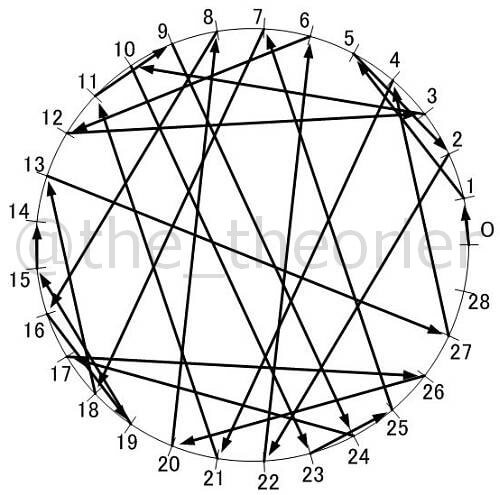
160827_07_29-2

　{ \displaystyle p=29, r=2 }

 

 

　見ての通り, { \displaystyle p=29 } でこれだけ複雑になってしまいます.

 

　これらを見て何かひらめく方はいるでしょうか？

 

　文字や表だけで見る数学でも, 今回のような図を用いるアプローチで, それまで見えなかった(見づらかった)ものが見えてくることがあります.

　我々は例えば二次方程式と二次関数のグラフなどで, 既にこの考えを当たり前に行っています.

　「数学をやれば論理的思考がー」といったありきたりなことは言いたくありませんが, 矛盾しない程度に他の表現で評価し, "元に戻す"手法は数学に限らず他の分野でも役に立つことでしょう.

 

　最後の最後に, { \displaystyle p=5 } から { \displaystyle 29 } までの指数表を載せておきます(縦書き, 原始根は各々の正値最小).

 

  Ind
p=57111317192329
Nr=23223252
1 0 0 0 0 0 0 0 0
2 1 2 1 1 14 1 2 1
3 3 1 8 4 1 13 16 5
4 2 4 2 2 12 2 4 2
5   5 4 9 5 16 1 22
6   3 9 5 15 14 18 6
7     7 11 11 6 19 12
8     3 3 10 3 6 3
9     6 8 2 8 10 10
10     5 10 3 17 3 23
11       7 7 12 9 25
12       6 13 15 20 7
13         4 5 14 18
14         9 7 21 13
15         6 11 17 27
16         8 4 8 4
17           10 7 21
18           9 12 11
19             15 9
20             5 24
21             13 17
22             11 26
23               20
24               8
25               16
26               19
27               15
28               14

 

 

thetheorier