もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

　MENU

【iPhoneショートカット】数字のソートを利用して統計量を計算する

iOS iOS-iOS15 iOS-ショートカット

人気記事

f:id:thetheorier:20210926111815p:plain

　先日の投稿で数字を並び替える方法を紹介しました.

　これを利用して並び替えが前提の統計量などを計算するレシピを作ります.

ショートカット

ショートカット

Apple
仕事効率化
無料

※価格は記事執筆時のものです. 現在の価格はApp Storeから確認ください.

　レビュー時のiOSバージョン　：　iOS15.0.1

スポンサーリンク

既存のものも含める
レシピ
実行
〆

既存のものも含める

　いくつかの統計量は「統計を計算」アクションから簡単に計算できます.

　それ以外はこちらで工夫しなければなりません.

レシピ

f:id:thetheorier:20210926112342p:plain

　まず評価したい数のデータを用意します.

　今回は「テキスト」アクションに直書きです.

f:id:thetheorier:20210926112429p:plain

　続いて「リスト」アクションに各種統計量の項目を並べます.

　今回は思いついた順に

最小値
最大値
平均値
中央値
四分位数
最頻値
分散
標準偏差
歪度
尖度
中点値
範囲

の12項目です.

　各々を単独で計算したかったのですが全体の処理に時間がかかってしまうため一部は他を流用することにします.

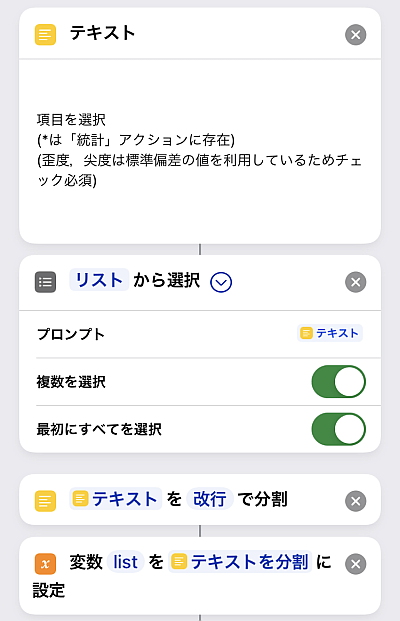
f:id:thetheorier:20210926112731p:plain

　統計値のリストを「リストから選択」で複数選択します.

　続いてデータを書き込んだ「テキスト」アクションを改行で分割したものを変数listで置きます.

　この時点でlistはきちんと昇順で並んでいるとは限らないため, ソートする必要があります.

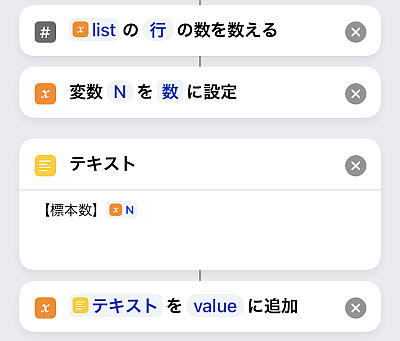
f:id:thetheorier:20210926113019p:plain

　その前にいくつかの情報は先に取得しておきます.

　まずはlistの行数, つまりデータの標本数です.

　すべての情報は変数valueに追加することにします.

f:id:thetheorier:20210926113141p:plain

　続いてlistの整数部の最大桁digitsを求めます.

　対象のデータが整数とは限らないため, listの最大値Maximumに対して「計算式」アクションを用いて

floor(log([Maximum])+1)

で最大桁数を求めます.

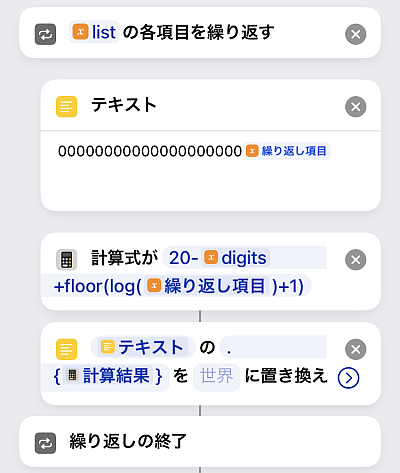
f:id:thetheorier:20210926113535p:plain

　前回の投稿に倣い, 各データを0埋めします.
　整数でないことを想定し, 最大桁で右から最大桁文字取り出すのでなく, 先頭から

[0埋めで使った0の文字数]-digits+floor(log([繰り返し項目])+1)

の分だけ文字を取り除くことになります(第3項は繰り返し項目の整数部桁数).

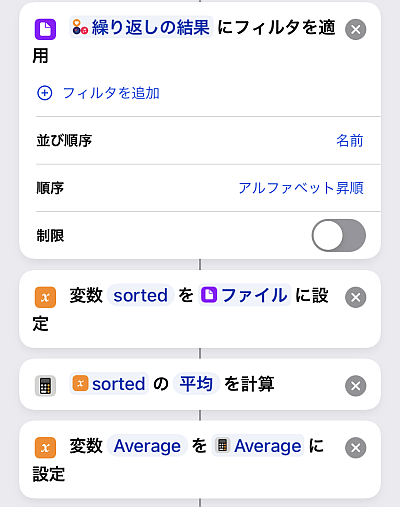
f:id:thetheorier:20210926114059p:plain

　こうして0埋めして整数部を揃えたデータリストに対して「ファイルにフィルタを適用」で名前に対して昇順に並び替えます.
　結果を変数sortedで置きます(「ファイル」の種類を数字にしておくことを忘れずに).

　今後はこのソート済みのデータsortedを使って色んな統計量を計算することになります.

　また後の処理の簡約化のために, この時点で平均値を求めておきます.

　ここからは具体的な統計量を求めていきます.

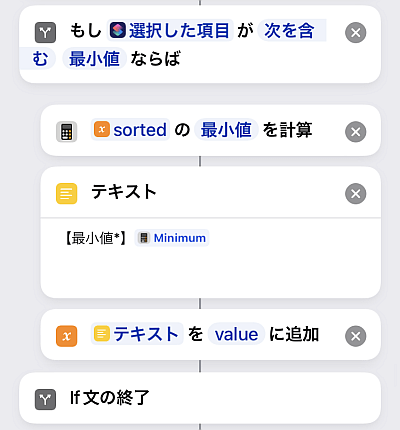
f:id:thetheorier:20210926114424p:plain

　まずは最小値です.

　最小値は「統計を計算」アクションに対応しているためこれを使います.

　「テキスト」アクションで体裁を整え, 変数valueに追加します(この処理は今後も共有なので以降の説明は省略します).

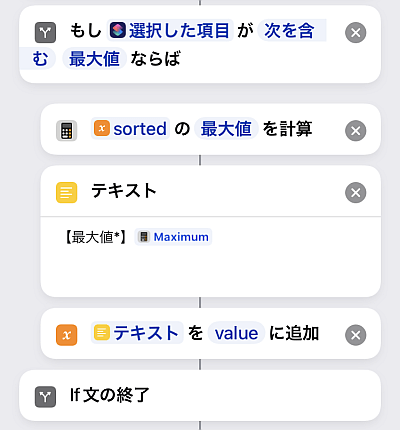
f:id:thetheorier:20210926114641p:plain

　最大値も同様です.

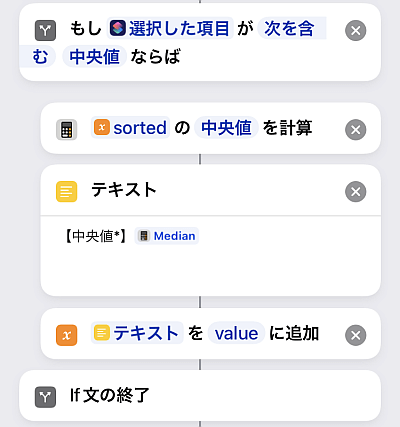
f:id:thetheorier:20210926114728p:plain

　中央値も「統計を計算」アクションを使います.

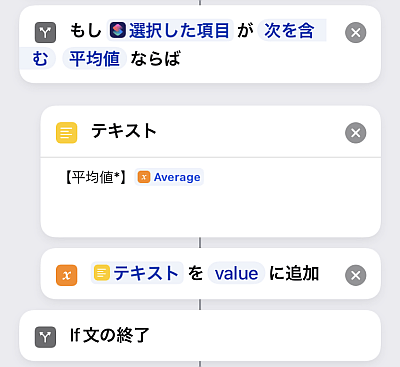
f:id:thetheorier:20210926114815p:plain

　平均値も「統計を計算」アクションに対応していますし, そもそも上で計算済みなのでそれを使います.

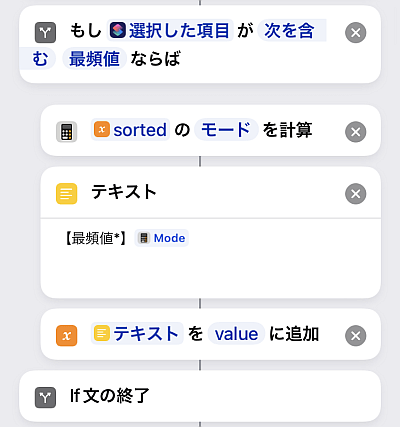
f:id:thetheorier:20210926114915p:plain

　最頻値(モード)も「統計を計算」アクションにあります.

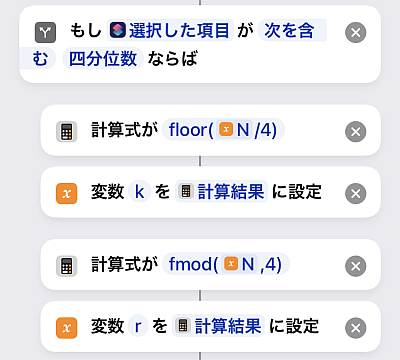
f:id:thetheorier:20210926115004p:plain

　中央値以外の四分位数 $Q_1,Q_3$ は「統計を計算」アクションにないため, 何らかの方法で計算しなければなりません.

blog.thetheorier.com

　四分位数の定義は複数あり, それを抜きにしても何らかの形で場合分けは避けれられません.

　今回は上の記事の定義D, WikipediaやExcelで用いられる定義を採用します.

　計算のしやすさのためにデータ数を4で割ったときの商k, そして同じく4で割った余りのrを計算しておきます.

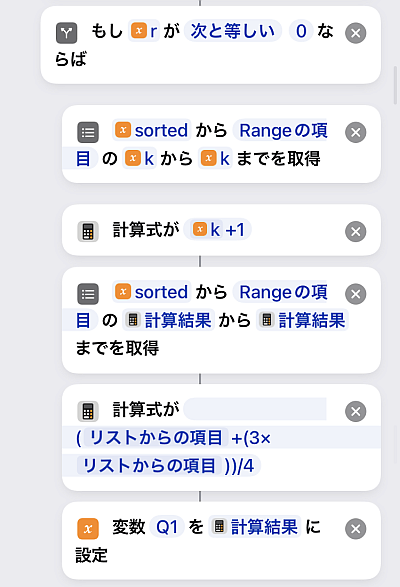
f:id:thetheorier:20210926150559p:plain

　まずはr=0, つまりデータ数が4の倍数のときです.
　このときの第一四分位数は今回の定義では

$\displaystyle Q_1=\frac{x_k+3_{k+1}}{4}$

で得られます.

　なのでsortedのデータのうちk番目とk+1番目が分かれば計算可能ですね.

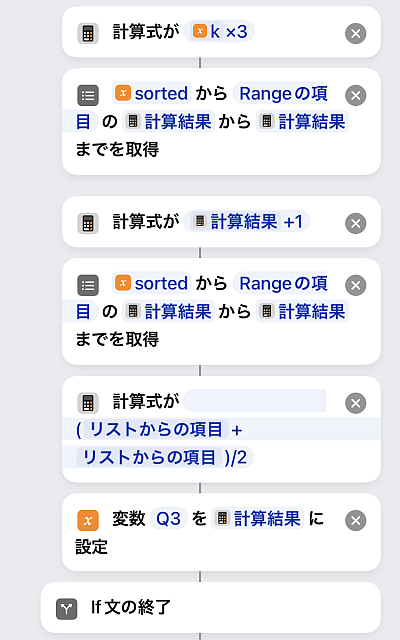
f:id:thetheorier:20210926151030p:plain

　同じく第三四分位数は

$\displaystyle Q_3=\frac{x_{3k}+x_{3k+1}}{2}$

です.

　この調子でr=1,2,3についても処理していきます.

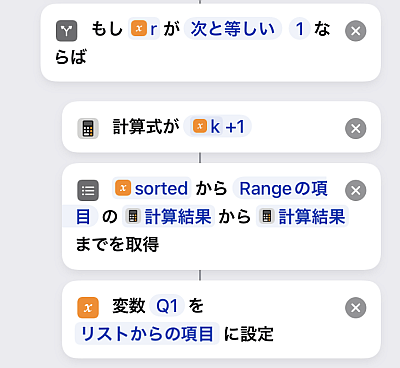
f:id:thetheorier:20210926151415p:plain

　続いてr=1の場合です.
　このとき第一四分位数は $\displaystyle Q_1=x_{k+1}$ です.

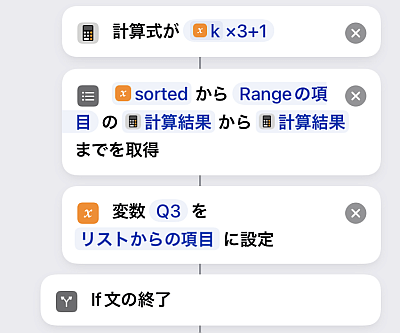
f:id:thetheorier:20210926151625p:plain

　同じく第三四分位数は $\displaystyle Q_3=x_{3k+1}$ です.

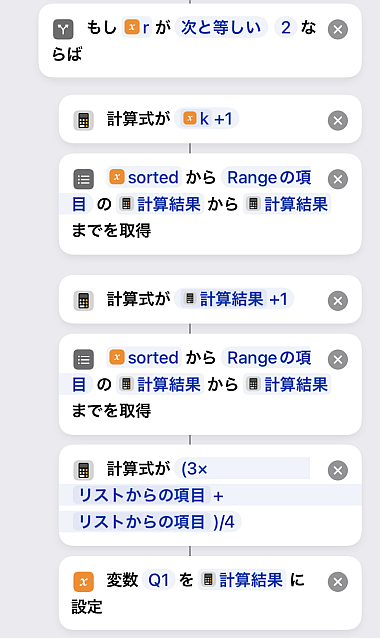
f:id:thetheorier:20210926151913p:plain

　次はr=2の場合です.
　このとき $\displaystyle Q_1=\frac{3x_{k+1}+x_{k+2}}{4}$ になります.

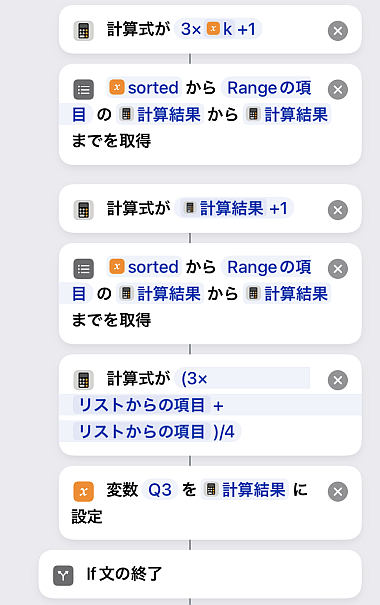
f:id:thetheorier:20210926152048p:plain

　同じく $\displaystyle Q_3=\frac{x_{3k+1}+3x_{3k+2}}{4}$ です.

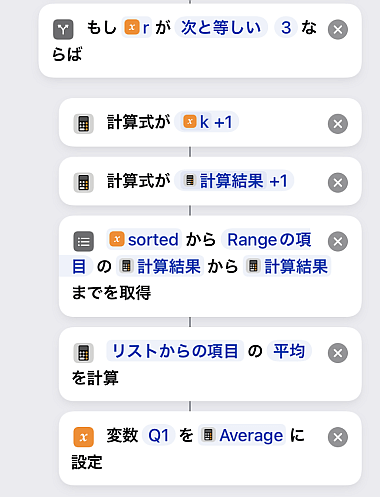
f:id:thetheorier:20210926152210p:plain

　最後にr=3の場合です.
　このとき $\displaystyle Q_1=\frac{x_{k+1}+x_{k+2}}{2}$ となります.

　今更ですが隣同士ですからこうして「リストから項目を取得」で2つ拾ってきて平均を取ればアクションが一つ少なくなります.

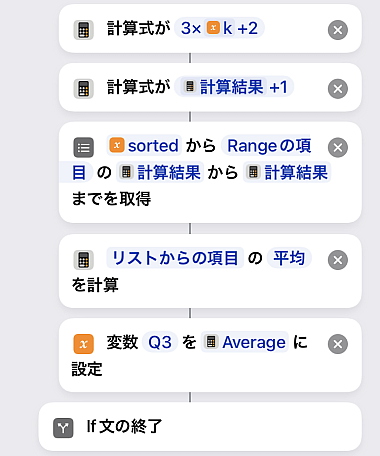
f:id:thetheorier:20210926152329p:plain

　 $\displaystyle Q_3=\frac{x_{3k+2}+x_{3k+3}}{2}$ となります.

　四分位数はこれで全部ですね.

f:id:thetheorier:20210926152948p:plain

　最後に四分位範囲 $Q_3-Q_1$ も計算してvalueに追加します.

　これで四分位数関連は終わりです.

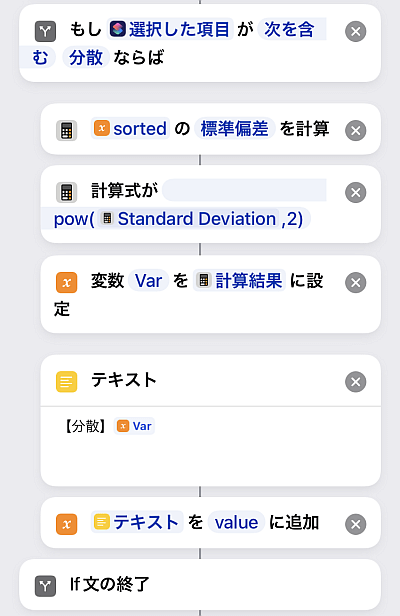
f:id:thetheorier:20210926161920p:plain

　続いては分散です.

　ショートカットでは「統計を計算」に標準偏差があり, 分散はこの2乗であることから求めます.

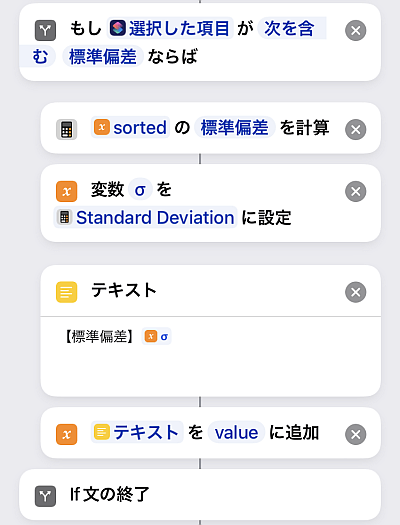
f:id:thetheorier:20210926162618p:plain

　標準偏差は「統計を計算」アクションにあるのでこれを使います.

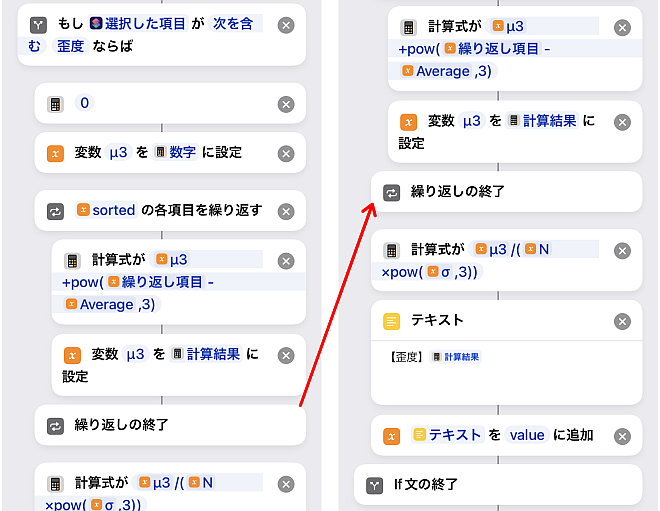
f:id:thetheorier:20210926154752p:plain

　次は歪度です.

　歪度は

$\displaystyle \frac{1}{n}\sum_{i=1}^n\left( \frac{x_i-\mu}{\sigma} \right)^3$

で定義され(μは平均、σは標準偏差), データが正規分布からどれだけ歪んでいるかを表す統計量です.

　nとσは単独固定値なので最後に計算します.

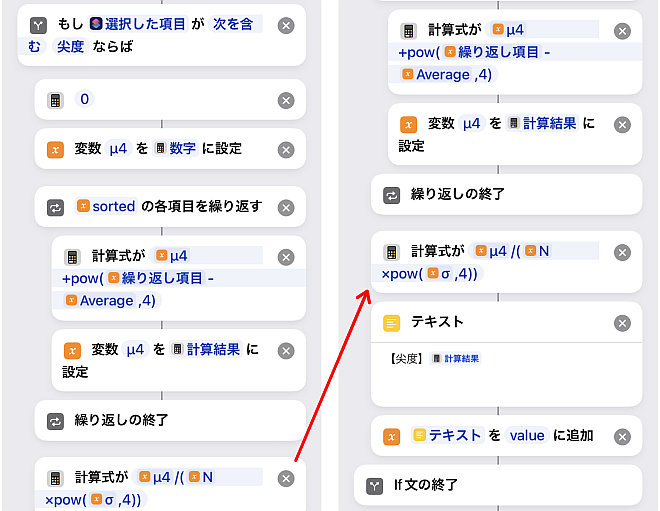
f:id:thetheorier:20210926162940p:plain

　次は尖度です.

　歪度が3乗だったのに比べこちらはそのまま4乗に変わります.

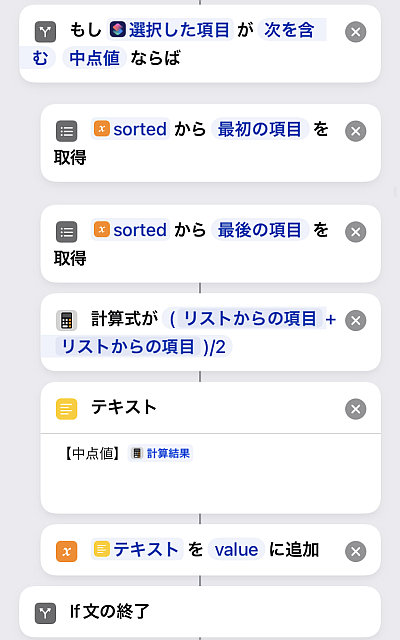
f:id:thetheorier:20210926163124p:plain

　次は中点値です.

　データのうち最小値と最大値の算術平均をとります.

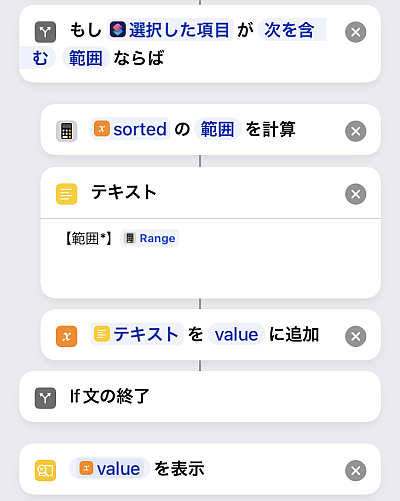
f:id:thetheorier:20210926163525p:plain

　最後は範囲(モード)です.

　「統計を計算」アクションになるのでそのまま使います.

　最後に変数valueを表示して終わります.

実行

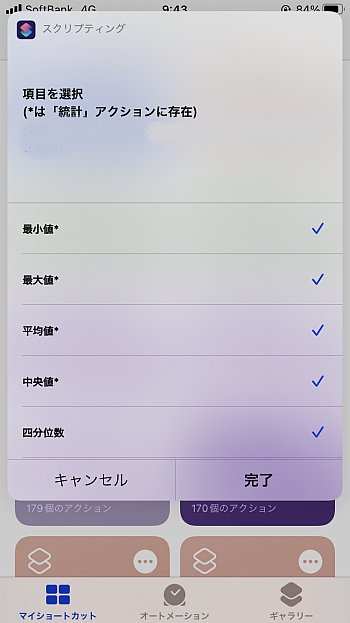
f:id:thetheorier:20210926164452p:plain

　あとは実行して確かめるだけです.

f:id:thetheorier:20210926165001p:plain

　問題なければこのようになります.

〆

　色々詰め込んだせいで, 今回の例のようなデータ数300でも結構な時間かかります.

　目的に応じて項目を減らした方が良いですね.