もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】0は自然数に含むのか？

iOS 数学

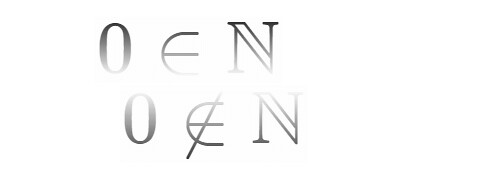
0 zero natural number

　今回は0と自然数の話です.

 

 

スポンサーリンク

 

 

自然数に0は含まない？

　質問サイトなどでもしばしば見られることですが, { \displaystyle 0 } は自然数なのでしょうか？

 

 

日常・歴史的視点

　例えばモノを数える時を考えると, { \displaystyle 0 } は考える必要がないから「含まない」と言われますね.

 

　しかし考え方によっては「数える前」は { \displaystyle 0 } ですし, 指を折って数えるケースも, 考え方によってはジャンケンで言うところの「グー」の状態を { \displaystyle 0 } とする解釈が可能です.

　「そんな状況考えなくて良いだろう」と言われればそれまでですが.

　しかし「そのように考えること」は可能です.

 

　またそもそも「数を数える」歴史より, { \displaystyle 0 } の概念が発見された時代は遥かに「新しい」と言えます.

　それまでは { \displaystyle 0 } に相当する概念は国地域時期によって様々でした.

　{ \displaystyle 0 } を認めるにしても自然数の仲間入りにするかはまた別の話でした.

 

　これは言うなれば数学の「歴史」, 言いかえれば「古典」であり, 現代数学のそれと全く一致するとは限りません(「古典」が不要であるというわけではありません).

　よく言われる「{ \displaystyle 0 } は存在しない数」「虚数は実在しない数」などというのは正に「古典的解釈」の典型です.

　当時はこれを数と見做すに足る「根拠」は言うまでもなく「体系」を「知りませんでした」, 故に未知としたり無, 非実在と(発見した者や「彼」に納得した者以外は)見なさざるを得なかったのです.

 

　今, 我々は当たり前に { \displaystyle 0 } や 負数, 虚数を使っています.

　使わざるとも結果的にその恩恵に預かったモノを利用しています.

 

　今回に限らず, 概念の理解に現代数学に基づくか古典であるによって結果が異なる事があります.

　これから学ぶ皆さんは勿論, そうでない方も(未知の概念は兎も角として)本来はその分別をつけるべきなのです.

 

 

ペアノ

　結局のところ, このような数そのものに立ち入る話は公理・定義のレベルであり, 「なぜ」と問うても証明のように自明であったり演繹的に導かれるようなものではありません.

　(現代)数学における「自明であること」とそうでないものの線引きは, 例えば読み手の学術レベルであったり「わざわざ説明することではないと判断したり…と様々ではありますが, 「当たり前」を構築する難しさの好例として, 自然数が挙げられることはしばしばでしょう.

　現に皆さんは「自然数の定義(公理)」を説明出来るでしょうか？

　普段当たり前に扱う「数」そのものを特徴づける性質を挙げ, それで問題なく定義されているか…

　結果的にペアノという人物によって, 公理化が成されました.

 

[公理：ペアノ]

　集合 { \displaystyle \mathbb{N} } が自然数であるとは, 次の条件を満たすものを言います.

 

  1. はじまりの数に相当する数が存在する ({ \displaystyle 0_{\mathbb{N}} } とでもします)
  2. 任意の { \displaystyle \mathbb{N} } の要素 { \displaystyle n } には, { \displaystyle n } の後者に相当する数が存在する ({ \displaystyle \text{suc}(n) } と書きます)
  3. { \displaystyle 0_{\mathbb{N}} } はいかなる自然数の後者でない
    { \displaystyle \Leftrightarrow\, \text{suc}(0_{\mathbb{N}}) } は存在しない
  4. 任意の自然数 { \displaystyle a,b\in\mathbb{N} } について, { \displaystyle \text{suc}(a)=\text{suc}(b)\,\Rightarrow\, a=b } が成り立つ(単射)
  5. 自然数 { \displaystyle \mathbb{N} } は上記4つを満たす最小の集合である

 

　ここにおいて, { \displaystyle 0_{\mathbb{N}} } を { \displaystyle 0 } とする根拠は何処にもありません.

　では { \displaystyle 1 } でも良いのでしょうか？結論としては問題ありません.

 

　しかしもっと突き詰めれば,  { \displaystyle 0 } や { \displaystyle 1 } という「文字」にする根拠があるのか？…という話になります.

　日常当たり前に使っている10進法の10個のアラビア数字である必要はあるのか, 英語や漢数字のそれでもよいのでは？いやいや他の文字, 記号で良いのでは？…とキリがありません.

 

「始まりの数」を { \displaystyle 0 } とするか { \displaystyle 1 } とするかが賛否両論である以前に, そもそも「始まりの数とは何ぞや」と言うことに, それが具体的に何であるか…ということにペアノの公理は答えませんし, 何よりそれが0であるか1であるかに本質的な違いはありません.

　しかし何らかの文字・記号で表記しなければ我々が理解出来ません, 然るにそれを表現するために妥当であろう { \displaystyle 0 } や { \displaystyle 1 } を宛がっているに過ぎないのです.

　それゆえ各々の都合でどちらにしても構わないとも解釈できます.

　歴史が, 慣例が違えばこの何れでも無かったかもしれません.

　これらに { \displaystyle 0 } や { \displaystyle 1 } という文字が使われたのは, 簡素に言ってしまえばただの結果論です.

 

　{ \displaystyle 0 } や { \displaystyle 1 } という「文字」と, それに相当する概念は必ずしも一致しません.

　概念として「始まりの数」や「零元」自体を万人が理解しても, それを表す「文字」は国地域によって異なる事は, 多くの方が同意することでしょう.

　かの高木貞治氏が著書で主張したように, アラビア圏ではそれを { \displaystyle LaTe0, 1 } と表し, 我々日本人は(漢字ならば)零, 一と表すと「約束」したのです.

 

 

「当たり前」を問う

　我々は既に, これが当たり前であることを知っています.

　それ故に「なぜ」と問われるとその「当たり前」が先行し, 「なぜ」への対応に苦慮します.

　それは他で例えれば「ある関数が図形を定義し, グラフとして表現できる」事を, 「数学らしい説明」抜きに知っていることと似ています.

 

　「そう言うモノ」で誤魔化せない「当たり前」を説明する, 体系付けるのは非常に難しいです.

 

　問うだけなら簡単なのに.

 

thetheorier