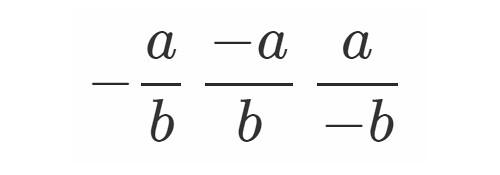
タイトルは分数としましたが簡単に有理数とします.
スポンサーリンク
分母や分子に付く?付かない?
質問サイトでもあたまに見かける話題です, つまり
は等しいのかどうか…です.
後者の二つについては比較的易しいでしょう, 有理数 について
が成り立つこと, 先日も紹介したマイナス×マイナス
により成り立ちます.
よって示すのは例えば のみで十分です.
というのは
の加法逆元に他なりません, 有理数の自然な加法・乗法の定義は
であり, 加法単位元は ですね.
従って任意の における加法逆元
は
を満たします.
この は(存在するならば)上の意味で
を表すわけです.
さて上を整理すると
となります.
例えば とすれば左辺は
となり, 整理して
, これは
により に等しいです.
然るに は
に等しいことが分かりました.
よって推移律より
が成り立ちます.
〆
数式としては別モノですが, 各々は紛れもなく等しいです.
どの表記が正しいとか間違っているとかではなく, 「どれが都合が良い」というだけでしかありません.
