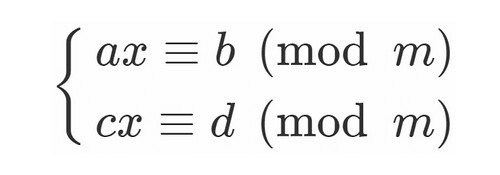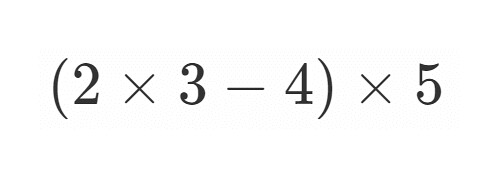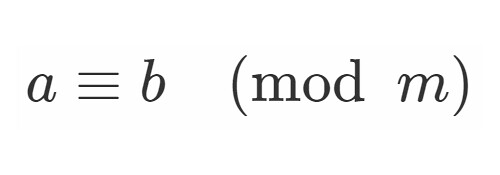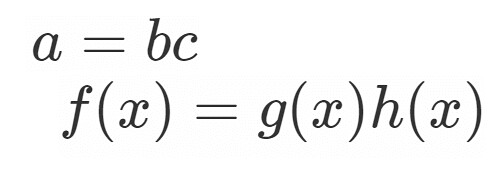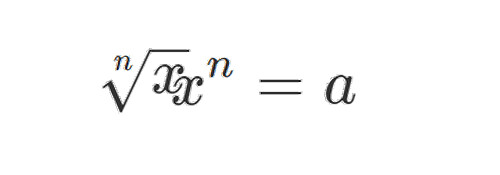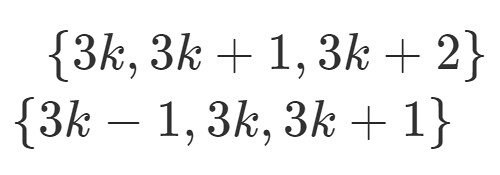【ショートカット】入力した日時の曜日を求める【ツェラーの公式】

　今回はツェラーの公式を用いて曜日を求めるショートカットを作ってみます.

ショートカット

• Apple
• 仕事効率化
• 無料
• 

※価格は記事執筆時のものです. 現在の価格はApp Storeから確認ください.

　レビュー時のバージョン　：　v2.1.1

スポンサーリンク

---

ツェラーの公式

　ツェラーの公式は日時の曜日を求める公式として一時期映画を通じて有名になりました.

　手計算でももちろん可能ですがショートカットに任せれば計算違いもありません.

ツェラーの公式 - Wikipedia

ツェラーの公式（ツェラーのこうしき、 英: Zeller's congruence）とは 西暦（ グレゴリオ暦または ユリウス暦）の 年・ 月・ 日から、その日が何 曜日であるかを算出する公式である。 クリスティアン・ツェラー ( Christian Zeller ) が考案した。 ユリウス通日 を求め、そこから曜日を求める計算と本質は同じである。

　計算式はWikipediaにあるものを参考にしました.

　1月と2月についてはそれぞれ前年の13月, 14月という扱いにすることに注意します.

　上記によって  を求め, 例えば  が  なら日曜日,  なら月曜日…となります.

フロー

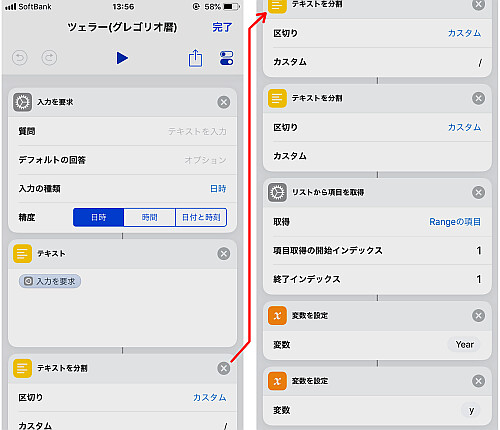
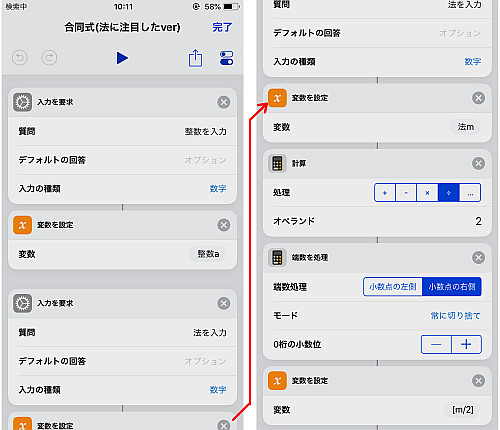
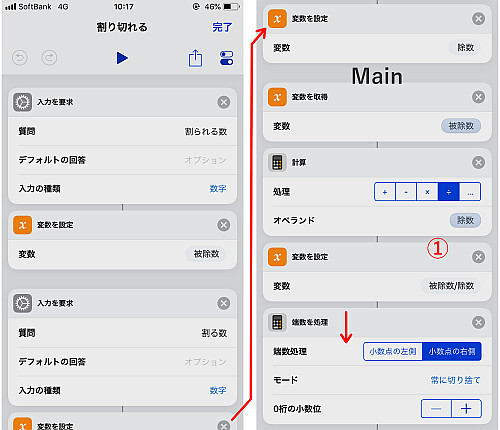
　まず「入力を要求」で「日時」を入力させます.

　公式では年月日をバラバラに扱うため, 一度「テキスト」に移し, 「テキストを分割」でバラして変数として代入しておきます.

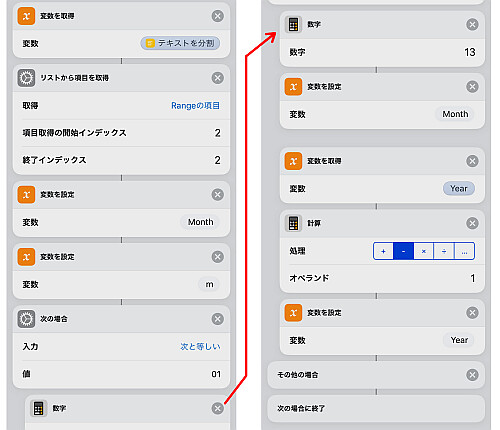
　先程指摘した通り, 1月と2月についてはそのままでは扱えないため, 変数を1つ余分に用意し, 演算用として使います.

　1月の場合は13に置き換え, 年数の変数も1つ減らします.

　2月の場合は14に置き換え, 同じく年数を1つ減らします.

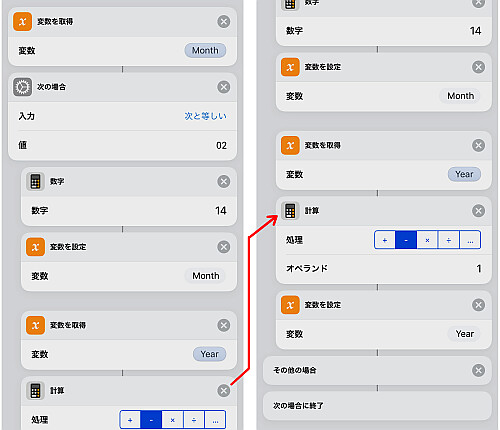
　ここまでが1月, 2月に対応した年, 月の内部変更になります.

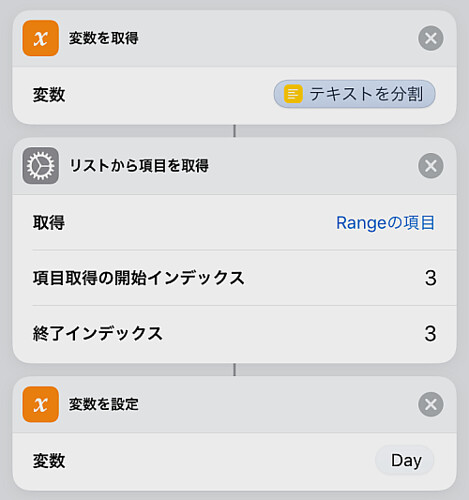
 最後に「テキストを分割」3行目を取り出して日数を取得します.

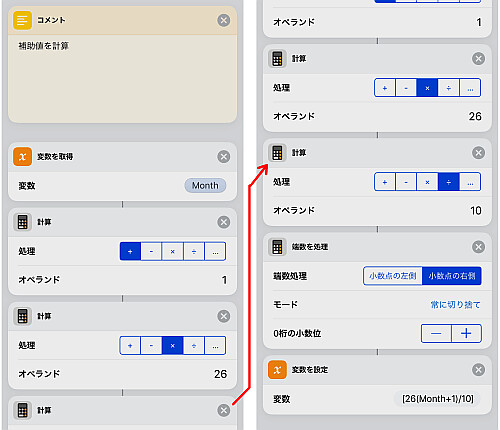
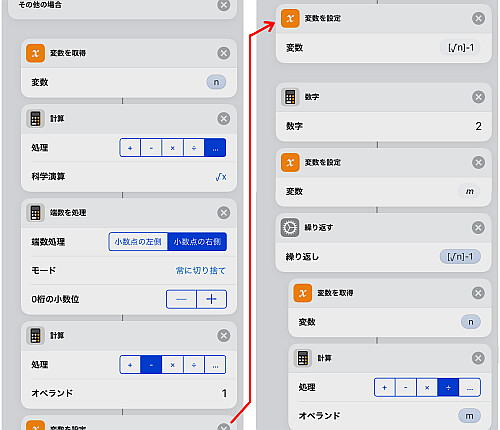
　準備が整ったので必要な記号式から順番に計算します.

　画像ではまず  を計算しています.

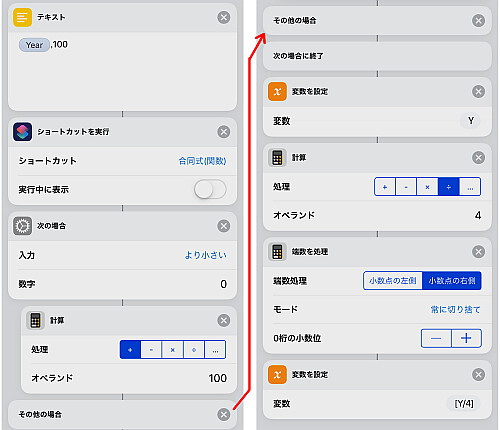
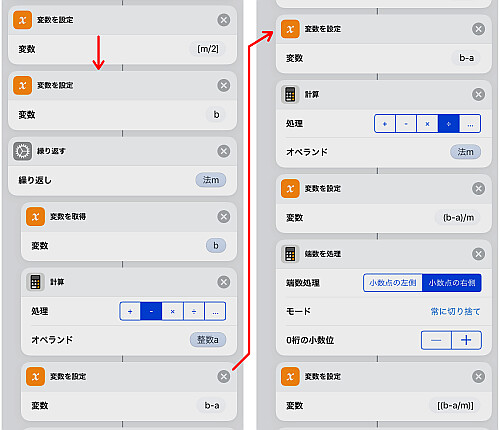
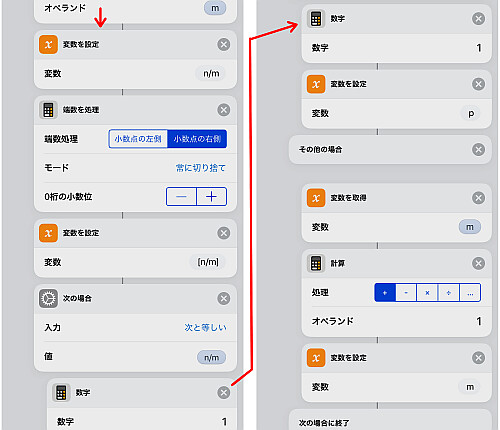
　続いて  および  を計算します.

　ここで使用している合同式の関数は絶対値最小剰余を返すため, 結果が負数の場合法  を足すことで正値最小剰余に直しています.

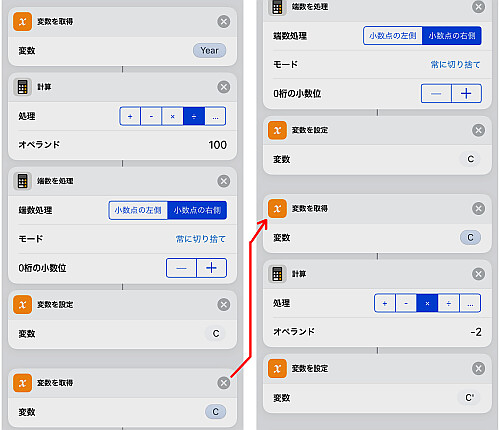
　続いて  を計算します.

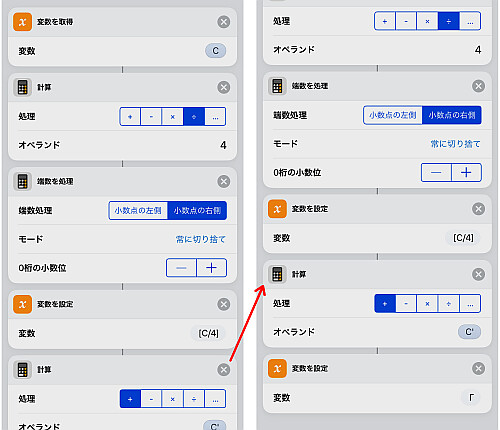
　最後に  を計算します.

　これで道具は揃いました.

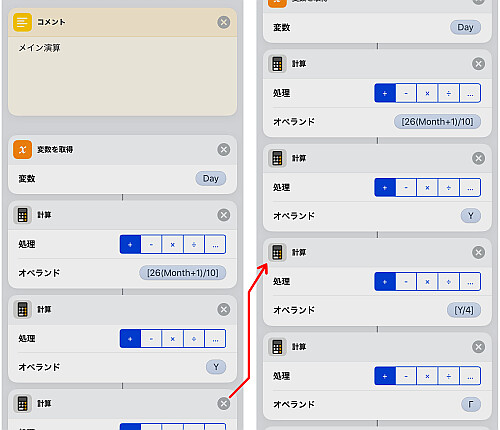
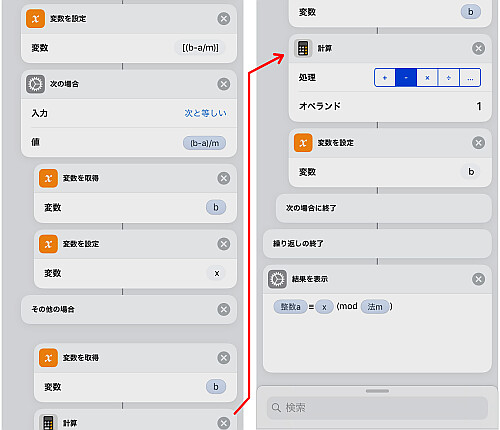
　前述までに用意した各値  を足し合わせます.

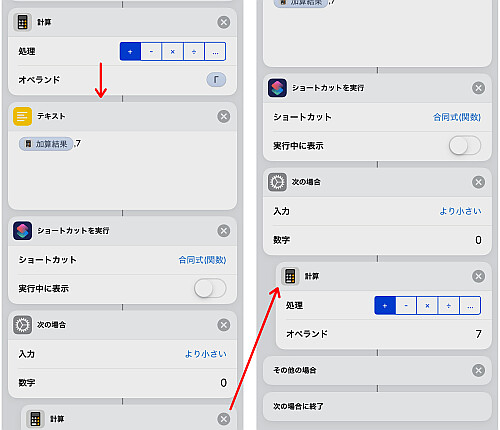
　結果を法  で整除します.

　やはり今回用意した合同式の関数は絶対値最小剰余で返すため, 結果が負数の場合は法である  で足します.

　これで  が確定しました.

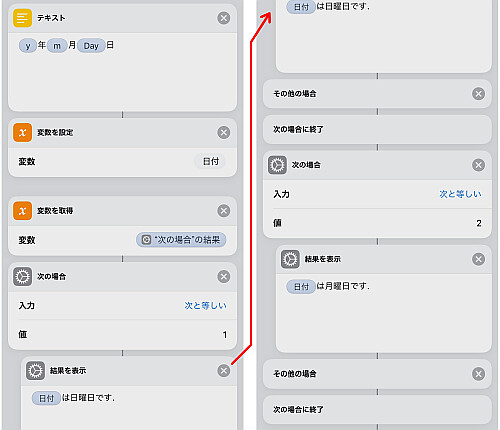
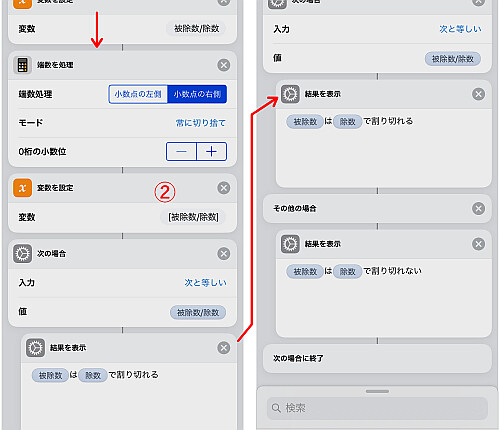
　「テキスト」アクションを用いて元の日付を構成します.

　「入力を要求」の結果をそのまま利用すると, 時刻までついてきてしまうための措置です.

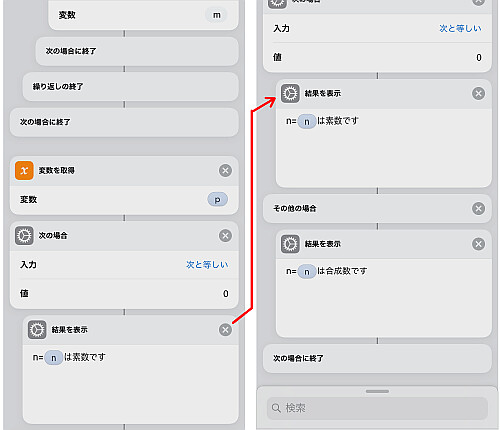
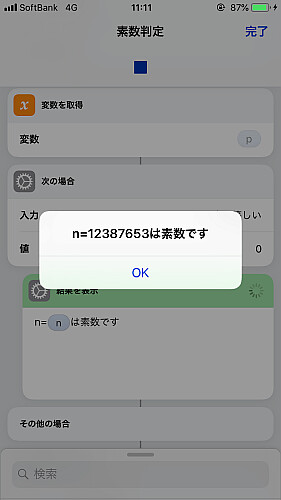
　その後先程得られた の値に応じて結果を表示します.

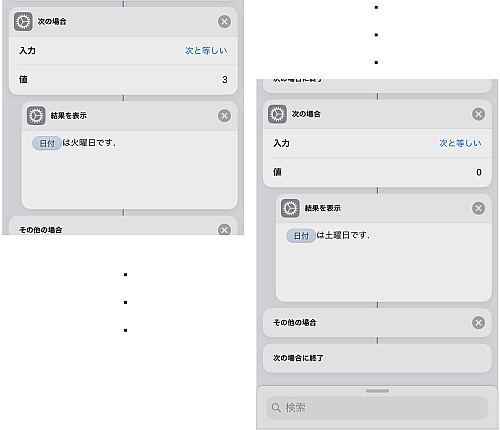
　7つの曜日すべてに対して書き終えれば完了です.

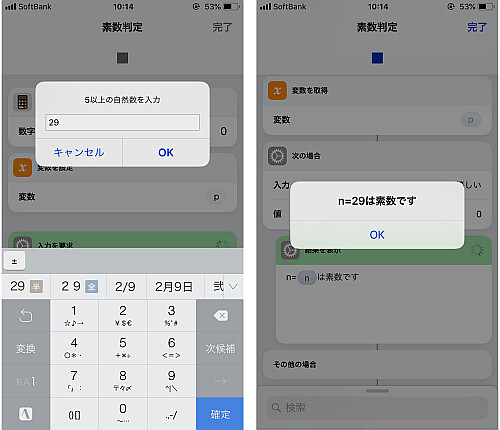
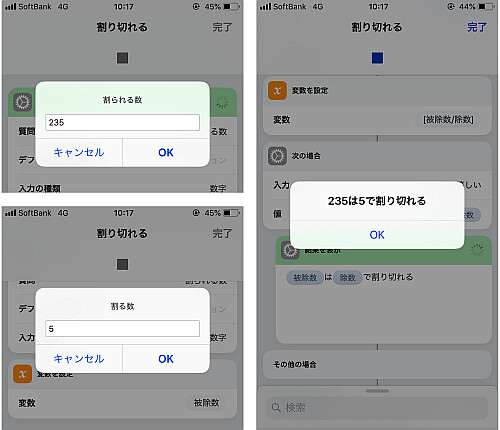
実行

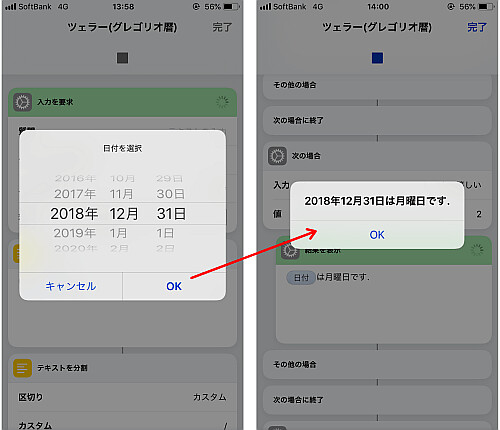
　実行して結果が正しいことを確かめます.

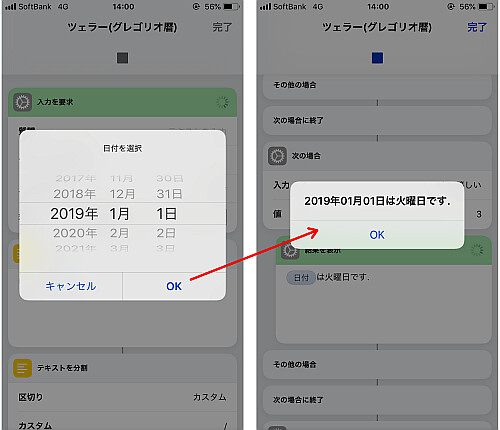
　1月, 2月の処理も問題なさそうです.

〆

　アクション数は104と多いですが, 一つ一つは負担の少ないアクションのため処理時間は1秒とかかりません.

　今回用いた公式はグレゴリオ暦に遵守したもののため, Wikipediaにある通り西暦1582年以降をサポートしています.

【ショートカット】合同式を計算するショートカット

　今回は合同式を計算するショートカットを作ってみました.

　具体的には入力した整数と法における絶対値最小剰余を求めます.

ショートカット

• Apple
• 仕事効率化
• 無料
• 

※価格は記事執筆時のものです. 現在の価格はApp Storeから確認ください.

　レビュー時のバージョン　：　v2.1

スポンサーリンク

---

「割り切れる」を再再利用

　今回も先日作った「割り切れる」の考え方を使います.

　そもそも合同式の定義そのものですね, 具体的に書くと, 整数  の差  が法  の倍数であるとき,

でした.

　つまり与えられた整数  と法  について, 値  が整数となるような整数  が求める結果です.

フロー

　まず整数  と法  を「入力を要求」によって与えます.

　拘る人はここで  や が整数となるようエラーチェックしましょう.

　続いて法  を用いて値 を計算します. 

　今回は「絶対値最小剰余」, つまり法  であれば

となるように取りたいため後ろである  から繰り返し, 値を1だけ減らして繰り返しを戻ります.

　なので正値最小剰余が欲しいならここは  にし, 繰り返しの際は1だけ値を増やして繰り返しを戻ります.

　上の説明の通りで繰り返し用に変数  に値 続けて定義します.

　次に「繰り返す」のアクションで繰り返し回数を法である  にします.

　繰り返しの中で  と  を計算します.

　 ならばその が求める結果なので別の変数(今回はx)に代入します.

　等しくなければ  を  だけ引き, 繰り返しに戻ります.

　正置最小剰余で求めたい場合は先の  の値に加え, ここで  減らすのではなく  増やすことになります.

　これで求める値  が決定したので「結果を表示」などで表示して完了です.

実行

　実行して正しいことを確認します.

　大きな値があってもそれなりにやってくれます.

〆

　余裕があれば指数の時のバージョンも作ってみたいです.

URLスキームについてはこちら

[Search]iPhone URLスキーム -The theoryの戯言

iPhoneのURLスキームを検索して一覧表示できます. リクエストは内容に応じてお答えします.

【ショートカット】素数判定をするショートカット

　今回は先日紹介した割り切れるかどうかを判定するアイデアを素数判定に利用します.

　なお今回も「自然数」のことを「正整数」として扱います.

ショートカット

• Apple
• 仕事効率化
• 無料
• 

※価格は記事執筆時のものです. 現在の価格はApp Storeから確認ください.

　レビュー時のバージョン　：　v2.1

スポンサーリンク

---

素数判定のアイデア

　まずは素数の定義から振り返りましょう.

　自然数  は  と  という, 少なくとも2つの「自明な(正)約数」を持ちます.

　なお  は自分自身を除く任意の自然数を, そして  は自分自身ただ一つを正約数に持つ特殊な数です.

　自然数  の中には自明な約数以外の正約数があります, これを「真の約数」と言います.

　自然数  が真の約数を持たないとき,  を素数, 真の約数を持つとき合成数と呼びます.

　素数  は自明な正約数を持ちませんから, 先日の「割り切れる」に倣えば

の  個はいずれも整数ではありません.

　但し  はこの限りではないためここからは  を奇素数とします.

　加えて自然数 は高々　 までの自然数で割り切れます.

　仮に自然数 が2つの自然数　 の積と等しいとき,

により,　 の約数　 が　 以下であることが分かります.

　従って実際には自然数  について

の 個とその床関数(ガウス記号)の結果が等しいかどうかをチェックすれば が素数であるかどうかがわかるということです.

　予めfalseにしたフラグをつくり, 一つでも一致するならtrueに立てて, falseのままなら素数と判断できます.

フロー

　まずイニシャルとして素数判定用の変数 に, デフォルト値として  (false) と置きます.

　またフローの都合上, 自明である  を弾くために「入力を要求」では  以上の自然数を要求させます.

　そうでない場合は「次の場合」を利用して再び自分自身のショートカットを呼び出すことではじめからやり直します(「実行中に表示」はオフにするとスムーズに移行します).

　ここからがメインのフローです.

　改めて「入力を要求」で得た値  を入力に代入し, 「計算」と「端数を処理」を組み合わせて  を計算します(  の誤りでしたが1つ余計に処理している以外結果に支障はありません).

　続いて先程あった

の分母に合わせて繰り返しを行うため, 変数  に  を代入します.

　素数(候補)である  より と  を計算し, 等しければ 素数  に (true) を立て, 等しくなければ  は何もせず  に  を加えて次の繰り返しに戻ります.

　すべての繰り返しによって  が  になっていたら  は素数でない(=合成数),  のままなら素数ということになります.

実行

　実行して結果が正しいことを確かめます.

　それなりに大きな数も結果を返してくれますが, 例えば画像の  の結果が変えるまで約5分34秒かかりました.

〆

　一つの結果を得るためにどうコーディングするかは一通りではありません.

　結果処理時間が早いか, 全体のコードの多寡ないし他人から見てわかりやすいか…等々の違いがありえます.

　当然コード(今回ならアクション)が少なく, かつ大きな値までサポートし, 処理時間も早いのが理想です.

　今回ははじめに理屈ありきなのでアイデア次第ではもっとエレガントなものを作る人がおられるでしょう.

URLスキームについてはこちら

[Search]iPhone URLスキーム -The theoryの戯言

iPhoneのURLスキームを検索して一覧表示できます. リクエストは内容に応じてお答えします.

【ショートカット】割り切れるかどうかを判定

　今回は割られる数が割る数で割り切れるかどうかを判定するショートカットを作ってみました.

　なお本記事では「自然数」を「正整数」の意味で使うことにします.

ショートカット

• Apple
• 仕事効率化
• 無料
• 

※価格は記事執筆時のものです. 現在の価格はApp Storeから確認ください.

　レビュー時のバージョン　：　v2.1

スポンサーリンク

---

「割り切れる」をどう表現するか

　割られる数(被除数)  が割る数(除数)  で割り切れるということをどう判定するべきでしょうか？

　ショートカットには現在「余り」を求めるアクションはありません.

　1つの案としては, もし  が  で割り切れるなら, その商  が整数になることを利用します.

　逆に言えば  が  で割り切れないならば  は整数にならず小数となります.

　とすると商の床関数 , つまり  の小数点以下切り捨ては割り切れるとき等しくなり, そうでないときは異なります.

• が  で割り切れる 
• が  で割り切れない

　今回はこれを採用します.

フロー

　まず被除数と除数を「入力を要求」で取得します.

　続いてまず商 を求めます(①).

　商 が求まり, 結果が入力に残っているのでそのまま「端数処理」で小数点以下を切り捨て, これを  として取得します(②).

　2数を比較して等しいなら素数, そうでないなら素数でない(合成数)と表示すれば完了です.

　後は実行して結果が正しいか確かめます.

〆

　制限などは書いていませんが0や負数にも対応しています.

　高級言語なら例えば fmod(x,y) を判定して終わりですが, その中身をどうつくるべきかを考える意味ではアセンブリレベルのアクションだけで試行錯誤するのは面白いですね.

URLスキームについてはこちら

[Search]iPhone URLスキーム -The theoryの戯言

iPhoneのURLスキームを検索して一覧表示できます. リクエストは内容に応じてお答えします.

【数学】連立一次合同方程式の解法

　今回は連立一次合同方程式の解についてです.

スポンサーリンク

---

連立一次合同方程式を解く

　次の連立合同方程式を解くとします.

　ここで とします.

　(1)より, は任意の整数 を用いて

と表せます.

　これは (2) を満たすので

となります, つまり は の倍数なので, 任意の整数 を用いて

と表せます.

　ここで は共に を約数に持ちますから, の左辺全体も で割り切れることを考えると も で割り切れます, 従って (4) は法 において解を持ちます.

　これを

, つまり任意の整数 を用いて

とでもします.

　これを (3) に代入して

, つまり が の倍数ですから,

, これが解となります.

〆

　連立が3つ4つ…となる場合はこれを繰り返せば良い訳ですね.

【make10】テンパズル全パターン(0000～2999)

　好きな人は暇な時にやってると思います.

スポンサーリンク

---

make10とは

　make10もしくはテンパズルとは, 4つの数字と四則演算を用いて10をつくるゲームです.

　昔からある遊びで個人的にはmixiのとあるコミュニティで一時期ハマりました.

　ルールは上記にある通り

• 使用可能な数は1,2,3,4,5,6,7,8,9のみ
• 演算記号は四則演算のみ

が一般的ですがここから更に

• 0を含む
• 数の並び替え
• 隣り合う数を1つの数として扱う
• 括弧の使用
• べき乗や階乗の使用
• 数論的関数の使用

などなどを許可する特殊ルールなども存在します.

　一般ルールに基づけば9つの数と3つの演算記号を使用するため大まかに  組 通りとなります.

　また括弧を使用する場合は

の8通りの組み合わせが考えられます.

　しかし実際には例えば

 

のように整理することで等しくなる組み合わせも存在するため同じ4数であっても8通りの結果がすべて異なるとも限りません.

　これらを含むかどうかで組み合わせの数が異なりますし, また無用な括弧を使う必要がないと解釈できます.

計算してみた

　具体的に4数を指定してその組が10になるかどうかは一般ルールでもせいぜい  通りですが, 括弧を許可すると と一気に膨れ上がります(64通りでも十分面倒ですが).

　因みに先程のような「整理して等しくなる」ものを1つと見なす, もう少し言うと「なるべく括弧を使わないものを選ぶ」ようにすると  通りとなります(間違っていなければですが).

　というわけで実際にプログラムを組んで計算してみました.

　使用したのはRAD Studio 10.2, 以前使っていたC++ Builderの後継であり条件付きで無料配布されているものです.

　ルールは以下となります.

1. 使用可能な数は0,1,2,3,4,5,6,7,8,9の10個
2. 数の並び替えは別として扱う(演算記号の違いは別扱い)
3. 隣り合う数を一つと数として扱うことはしない(4数別々に扱う)
4. 括弧を使用, 但し整理して括弧を使わない式と等しくなるならば後者のみを採用
5. べき乗や階乗は使用しない
6. 数論的関数は使用しない

　補足しますが今回のルールでは  と  , また  と  などは区別されます.

　従ってこの類のサイトがたくさんありますが, どこまでを重複と見なすか…で組み合わせの数が全く異なることに注意してください.

(実際, mixiの某コミュニティではどこまでを許容するか, 重複とするか…はちょくちょくルールとして加筆・変更した上で楽しんでいました)

　結果は  通りとなりました, コーディングミスが無ければですが…

　結果が  となる  数の組 としての数は  組でした.

　実際の一覧は記事末に載せておきますね.

　因みに括弧を使わない場合は  通りで  組でした.

　整理すると以下となります.

	括弧あり	括弧なし
10になる数式の数
10になる4数の組み合わせ

　括弧が使えなくなると4数の組み合わせは1000程度しか落ちないのに10となる数式はおよそ半分にも落ちてしまうんですね.

　括弧があると10になる数式パターンが一気に増えるのがわかります.

　4数の組み合わせの総数は  ですからその割合は ということで大体半分は四則演算と括弧を使って10にできるということになります.

　括弧なしでも  割くらいは可能なんですね.

　因みに同じようにして1～10について計算したところ以下の結果となりました.

	括弧あり		括弧なし
	数式数	4数組	数式数	4数組
1	25,979	6,229	10,461	4,396
2	24,042	6,276	10,453	4,453
3	22,903	6,070	10,492	4,464
4	25,641	5,910	11,965	4,454
5	22,927	5,618	11,598	4,398
6	22,968	6,058	10,632	4,568
7	19,667	5,606	10,147	4,387
8	23,455	5,926	11,229	4,443
9	20,330	5,724	10,153	4,340
10	14,985	5,496	7,916	4,072

　1から10の中では4数の組はもちろん数式の数で10が極端に少ないようです.

　グラフにしてみると数式での違いがよくわかります.

make10の数式一覧

　上記で計算した, 4数を用いて10になる数式です.

　約1万5千ということでそのまま表示すると大変なので0xxx～9xxxで10等分にしました.

　それでもはてなブログの1記事辺りの文字数制限にひっかかるためまずは0000～2999までとなります.

0xxx

0000～0999

0+0+1+9
0-0+1+9
0×0+1+9
0+0+2×5
0+(0+2)×5
(0+0+2)×5
0+0-2×5
0-0+2×5
(0-0+2)×5
0-(0-2)×5
0×0+2×5
(0×0+2)×5
0+0+2+8
0-0+2+8
0×0+2+8
0+0+3+7
0-0+3+7
0×0+3+7
0+0+4+6
0-0+4+6
0×0+4+6
0+0+5×2
0+(0+5)×2
(0+0+5)×2
0+0-5×2
0-0+5×2
(0-0+5)×2
0-(0-5)×2
0×0+5×2
(0×0+5)×2
0+0+5+5
0-0+5+5
0×0+5+5
0+0+6+4
0-0+6+4
0×0+6+4
0+0+7+3
0-0+7+3
0×0+7+3
0+0+8+2
0-0+8+2
0×0+8+2
0+0+9+1
0-0+9+1
0×0+9+1
0+(1+1)×5
(0+1+1)×5
0+1+1+8
0+1+1×9
0+1-1×9
0+1×1+9
0+1×(1+9)
(0+1)×1+9
(0+1)×(1+9)
0+1÷1+9
(0+1)÷1+9
0×1+1+9
0÷1+1+9
0+1×2×5
(0+1)×2×5
(0+1×2)×5
0×1+2×5
(0×1+2)×5
0÷1+2×5
(0÷1+2)×5
0+1+2+7
0+1×2+8
0+1×(2+8)
(0+1)×2+8
(0+1)×(2+8)
0×1+2+8
0÷1+2+8
0-1+2+9
0+1+3×3
0+1-3×3
(0-1+3)×5
0-(1-3)×5
0+1+3+6
0+1×3+7
0+1×(3+7)
(0+1)×3+7
(0+1)×(3+7)
0×1+3+7
0÷1+3+7
0-1+3+8
0+(1+4)×2
(0+1+4)×2
0+1+4+5
0+1×4+6
0+1×(4+6)
(0+1)×4+6
(0+1)×(4+6)
0×1+4+6
0÷1+4+6
0-1+4+7
0+1×5×2
(0+1)×5×2
(0+1×5)×2
0×1+5×2
(0×1+5)×2
0÷1+5×2
(0÷1+5)×2
0+1+5+4
0+1×5+5
0+1×(5+5)
(0+1)×5+5
(0+1)×(5+5)
0×1+5+5
0÷1+5+5
0-1+5+6
(0-1+6)×2
0-(1-6)×2
0+1+6+3
0+1×6+4
0+1×(6+4)
(0+1)×6+4
(0+1)×(6+4)
0×1+6+4
0÷1+6+4
0-1+6+5
0+1+7+2
0+1×7+3
0+1×(7+3)
(0+1)×7+3
(0+1)×(7+3)
0×1+7+3
0÷1+7+3
0-1+7+4
0+1+8+1
0+1×8+2
0+1×(8+2)
(0+1)×8+2
(0+1)×(8+2)
0×1+8+2
0÷1+8+2
0-1+8+3
0+1+9+0
0+1+9-0
0+1+9×1
0+(1+9)×1
(0+1+9)×1
0+1+9÷1
0+(1+9)÷1
(0+1+9)÷1
0+1-9×1
0+1×9+1
0+1×(9+1)
(0+1)×9+1
(0+1)×(9+1)
0×1+9+1
0÷1+9+1
0-1+9+2
0+2×(1+4)
(0+2)×(1+4)
0+2×1×5
(0+2)×1×5
(0+2×1)×5
0+2÷1×5
(0+2)÷1×5
(0+2÷1)×5
0-2×(1-6)
(0-2)×(1-6)
0+2+1+7
0+2+1×8
0+2-1×8
0+2×1+8
(0+2)×1+8
0+2÷1+8
(0+2)÷1+8
0+2-1+9
0×2+1+9
0÷2+1+9
0+2×(2+3)
(0+2)×(2+3)
0+2+2×4
0+2-2×4
0×2+2×5
(0×2+2)×5
0÷2+2×5
(0÷2+2)×5
0+2+2+6
0+2×2+6
(0+2)×2+6
0-2+2×6
0-2×(2-7)
(0-2)×(2-7)
0×2+2+8
0÷2+2+8
0+2÷2+9
(0+2)÷2+9
0+(2+3)×2
(0+2+3)×2
0+2×(3+2)
(0+2)×(3+2)
0+2×3+4
(0+2)×3+4
0-2+3×4
0+2+3+5
0×2+3+7
0÷2+3+7
0-2×(3-8)
(0-2)×(3-8)
0-2+3+9
0+2×(4+1)
(0+2)×(4+1)
0+2+4×2
0+2-4×2
0+2×4+2
(0+2)×4+2
0-2+4×3
0+2+4+4
(0-2+4)×5
0-(2-4)×5
0×2+4+6
0÷2+4+6
0-2+4+8
0-2×(4-9)
(0-2)×(4-9)
0+2×5+0
0+2×(5+0)
(0+2)×5+0
(0+2)×(5+0)
0+2×5-0
0+2×(5-0)
(0+2)×5-0
(0+2)×(5-0)
0+2×5×1
(0+2)×5×1
(0+2×5)×1
0+2×5÷1
(0+2)×5÷1
(0+2×5)÷1
0×2+5×2
(0×2+5)×2
0÷2+5×2
(0÷2+5)×2
0+2+5+3
0×2+5+5
0÷2+5+5
0-2+5+7
0+2×(6-1)
(0+2)×(6-1)
0+2+6+2
0+2×6-2
(0+2)×6-2
0-2+6×2
0×2+6+4
0÷2+6+4
0-2+6+6
0+2+7+1
0+2×(7-2)
(0+2)×(7-2)
(0-2+7)×2
0-(2-7)×2
0×2+7+3
0÷2+7+3
0+2×7-4
(0+2)×7-4
0-2+7+5
0+2+8+0
0+2+8-0
0+2+8×1
0+(2+8)×1
(0+2+8)×1
0+2+8÷1
0+(2+8)÷1
(0+2+8)÷1
0+2-8×1
0×2+8+2
0÷2+8+2
0+2×(8-3)
(0+2)×(8-3)
0-2+8+4
0+2×8-6
(0+2)×8-6
0+2+9-1
0×2+9+1
0÷2+9+1
0-2+9+3
0+2×(9-4)
(0+2)×(9-4)
0+2×9-8
(0+2)×9-8
0+(3-1)×5
(0+3-1)×5
0+3+1+6
0+3+1×7
0+3-1×7
0+3×1+7
(0+3)×1+7
0+3÷1+7
(0+3)÷1+7
0+3-1+8
0×3+1+9
0÷3+1+9
0+(3+2)×2
(0+3+2)×2
0+3×2+4
(0+3)×2+4
0+3+2+5
0×3+2×5
(0×3+2)×5
0÷3+2×5
(0÷3+2)×5
0×3+2+8
0÷3+2+8
0+3-2+9
0+3×3+1
(0+3)×3+1
0+3+3+4
0×3+3+7
0÷3+3+7
0+3÷3+9
(0+3)÷3+9
0+3×4-2
(0+3)×4-2
0+3+4+3
0×3+4+6
0÷3+4+6
0-3+4+9
0+3+5+2
0×3+5×2
(0×3+5)×2
0÷3+5×2
(0÷3+5)×2
0+3×5-5
(0+3)×5-5
(0-3+5)×5
0-(3-5)×5
0×3+5+5
0÷3+5+5
0-3+5+8
0+3+6+1
0×3+6+4
0÷3+6+4
0-3+6+7
0+3×6-8
(0+3)×6-8
0+3+7+0
0+3+7-0
0+3+7×1
0+(3+7)×1
(0+3+7)×1
0+3+7÷1
0+(3+7)÷1
(0+3+7)÷1
0+3-7×1
0×3+7+3
0÷3+7+3
0-3+7+6
0+3+8-1
(0-3+8)×2
0-(3-8)×2
0×3+8+2
0÷3+8+2
0-3+8+5
0×3+9+1
0÷3+9+1
0+3+9-2
0-3+9+4
0+(4+1)×2
(0+4+1)×2
0+4+1+5
0+4+1×6
0+4-1×6
0+4×1+6
(0+4)×1+6
0+4÷1+6
(0+4)÷1+6
0+4-1+7
0×4+1+9
0÷4+1+9
0+4×2+2
(0+4)×2+2
0+4+2×3
0+4-2×3
0+4+2+4
0+(4-2)×5
(0+4-2)×5
0+4÷2×5
(0+4)÷2×5
(0+4÷2)×5
0×4+2×5
(0×4+2)×5
0÷4+2×5
(0÷4+2)×5
0-4+2×7
0+4-2+8
0+4÷2+8
(0+4)÷2+8
0×4+2+8
0÷4+2+8
0+4+3×2
0+4-3×2
0+4×3-2
(0+4)×3-2
0+4+3+3
0×4+3+7
0÷4+3+7
0+4-3+9
0+4+4+2
0+4×4-6
(0+4)×4-6
0×4+4+6
0÷4+4+6
0+4÷4+9
(0+4)÷4+9
0+4+5+1
0+4×5÷2
(0+4)×5÷2
(0+4×5)÷2
0×4+5×2
(0×4+5)×2
0÷4+5×2
(0÷4+5)×2
0×4+5+5
0÷4+5+5
0-4+5+9
0+4+6+0
0+4+6-0
0+4+6×1
0+(4+6)×1
(0+4+6)×1
0+4+6÷1
0+(4+6)÷1
(0+4+6)÷1
0+4-6×1
0×4+6+4
0÷4+6+4
(0-4+6)×5
0-(4-6)×5
0-4+6+8
0+4+7-1
0-4+7×2
0×4+7+3
0÷4+7+3
0-4+7+7
0+4+8-2
0×4+8+2
0÷4+8+2
0-4+8+6
0×4+9+1
0÷4+9+1
(0-4+9)×2
0-(4-9)×2
0+4+9-3
0-4+9+5
0+5×(1+1)
(0+5)×(1+1)
0+5×1×2
(0+5)×1×2
(0+5×1)×2
0+5÷1×2
(0+5)÷1×2
(0+5÷1)×2
0-5×(1-3)
(0-5)×(1-3)
0+5+1+4
0+5+1×5
0+5-1×5
0+5×1+5
(0+5)×1+5
0+5÷1+5
(0+5)÷1+5
0+5-1+6
0×5+1+9
0÷5+1+9
0+5×2+0
0+5×(2+0)
(0+5)×2+0
(0+5)×(2+0)
0+5×2-0
0+5×(2-0)
(0+5)×2-0
(0+5)×(2-0)
0+5×2×1
(0+5)×2×1
(0+5×2)×1
0+5×2÷1
(0+5)×2÷1
(0+5×2)÷1
0+5+2+3
0+5÷2×4
(0+5)÷2×4
(0+5÷2)×4
0-5×(2-4)
(0-5)×(2-4)
0×5+2×5
(0×5+2)×5
0÷5+2×5
(0÷5+2)×5
0+5-2+7
0×5+2+8
0÷5+2+8
0+5×(3-1)
(0+5)×(3-1)
0+5+3+2
0+(5-3)×5
(0+5-3)×5
0+5×3-5
(0+5)×3-5
0-5+3×5
0-5×(3-5)
(0-5)×(3-5)
0+5÷3×6
(0+5)÷3×6
(0+5÷3)×6
0×5+3+7
0÷5+3+7
0+5-3+8
0+5+4+1
0+5×(4-2)
(0+5)×(4-2)
0+5×4÷2
(0+5)×4÷2
(0+5×4)÷2
0-5×(4-6)
(0-5)×(4-6)
0×5+4+6
0÷5+4+6
0+5÷4×8
(0+5)÷4×8
(0+5÷4)×8
0+5-4+9
0+5+5+0
0+5+5-0
0+5+5×1
0+(5+5)×1
(0+5+5)×1
0+5+5÷1
0+(5+5)÷1
(0+5+5)÷1
0+5-5×1
0×5+5×2
(0×5+5)×2
0÷5+5×2
(0÷5+5)×2
0+5×(5-3)
(0+5)×(5-3)
0-5+5×3
0×5+5+5
0÷5+5+5
0-5×(5-7)
(0-5)×(5-7)
0+5÷5+9
(0+5)÷5+9
0+5+6-1
0+5×6÷3
(0+5)×6÷3
(0+5×6)÷3
0+5×(6-4)
(0+5)×(6-4)
0×5+6+4
0÷5+6+4
0-5×(6-8)
(0-5)×(6-8)
0-5+6+9
0+5+7-2
0×5+7+3
0÷5+7+3
0+5×(7-5)
(0+5)×(7-5)
(0-5+7)×5
0-(5-7)×5
0-5+7+8
0-5×(7-9)
(0-5)×(7-9)
0×5+8+2
0÷5+8+2
0+5+8-3
0+5×8÷4
(0+5)×8÷4
(0+5×8)÷4
0+5×(8-6)
(0+5)×(8-6)
0-5+8+7
0×5+9+1
0÷5+9+1
0+5+9-4
0-5+9+6
0+5×(9-7)
(0+5)×(9-7)
0+(6-1)×2
(0+6-1)×2
0+6+1+3
0+6+1×4
0+6-1×4
0+6×1+4
(0+6)×1+4
0+6÷1+4
(0+6)÷1+4
0+6-1+5
0×6+1+9
0÷6+1+9
0+6+2+2
0+6+2×2
0+6-2×2
0+6×2-2
(0+6)×2-2
0×6+2×5
(0×6+2)×5
0÷6+2×5
(0÷6+2)×5
0+6-2+6
0+6÷2+7
(0+6)÷2+7
0-6+2×8
0×6+2+8
0÷6+2+8
0+6+3+1
0+6÷3×5
(0+6)÷3×5
(0+6÷3)×5
0+6-3+7
0×6+3+7
0÷6+3+7
0+6×3-8
(0+6)×3-8
0+6÷3+8
(0+6)÷3+8
0+6+4+0
0+6+4-0
0+6+4×1
0+(6+4)×1
(0+6+4)×1
0+6+4÷1
0+(6+4)÷1
(0+6+4)÷1
0+6-4×1
0-6+4×4
0+(6-4)×5
(0+6-4)×5
0×6+4+6
0÷6+4+6
0+6-4+8
0+6+5-1
0×6+5×2
(0×6+5)×2
0÷6+5×2
(0÷6+5)×2
0+6×5÷3
(0+6)×5÷3
(0+6×5)÷3
0×6+5+5
0÷6+5+5
0+6-5+9
0+6+6-2
0×6+6+4
0÷6+6+4
0+6÷6+9
(0+6)÷6+9
0+6+7-3
0×6+7+3
0÷6+7+3
0-6+7+9
0+6+8÷2
0-6+8×2
0×6+8+2
0÷6+8+2
0+6+8-4
(0-6+8)×5
0-(6-8)×5
0-6+8+8
0×6+9+1
0÷6+9+1
0+6+9-5
0-6+9+7
0+7+1+2
0+7+1×3
0+7-1×3
0+7×1+3
(0+7)×1+3
0+7÷1+3
(0+7)÷1+3
0+7-1+4
0×7+1+9
0÷7+1+9
0+7+2+1
0+(7-2)×2
(0+7-2)×2
0+7×2-4
(0+7)×2-4
0+7-2+5
0×7+2×5
(0×7+2)×5
0÷7+2×5
(0÷7+2)×5
0×7+2+8
0÷7+2+8
0+7+3+0
0+7+3-0
0+7+3×1
0+(7+3)×1
(0+7+3)×1
0+7+3÷1
0+(7+3)÷1
(0+7+3)÷1
0+7-3×1
0+7-3+6
0×7+3+7
0÷7+3+7
0+7+4-1
0×7+4+6
0÷7+4+6
0+7-4+7
0+7+5-2
0×7+5×2
(0×7+5)×2
0÷7+5×2
(0÷7+5)×2
0+(7-5)×5
(0+7-5)×5
0×7+5+5
0÷7+5+5
0+7-5+8
0+7+6÷2
0+7+6-3
0×7+6+4
0÷7+6+4
0+7-6+9
0×7+7+3
0÷7+7+3
0+7+7-4
0+7÷7+9
(0+7)÷7+9
0×7+8+2
0÷7+8+2
0+7+8-5
0-7+8+9
0×7+9+1
0÷7+9+1
0+7+9÷3
(0-7+9)×5
0-(7-9)×5
0+7+9-6
0-7+9+8
0+8+1+1
0+8+1×2
0+8-1×2
0+8×1+2
(0+8)×1+2
0+8÷1+2
(0+8)÷1+2
0+8-1+3
0×8+1+9
0÷8+1+9
0+8+2+0
0+8+2-0
0+8+2×1
0+(8+2)×1
(0+8+2)×1
0+8+2÷1
0+(8+2)÷1
(0+8+2)÷1
0+8-2×1
0+8-2+4
0×8+2×5
(0×8+2)×5
0÷8+2×5
(0÷8+2)×5
0+8×2-6
(0+8)×2-6
0+8÷2+6
(0+8)÷2+6
0×8+2+8
0÷8+2+8
0-8+2×9
0+8+3-1
0+(8-3)×2
(0+8-3)×2
0+8-3+5
0-8+3×6
0×8+3+7
0÷8+3+7
0+8+4-2
0+8+4÷2
0+8÷4×5
(0+8)÷4×5
(0+8÷4)×5
0+8-4+6
0×8+4+6
0÷8+4+6
0+8÷4+8
(0+8)÷4+8
0×8+5×2
(0×8+5)×2
0÷8+5×2
(0÷8+5)×2
0+8+5-3
0+8×5÷4
(0+8)×5÷4
(0+8×5)÷4
0×8+5+5
0÷8+5+5
0+8-5+7
0+8+6÷3
0-8+6×3
0+8+6-4
0×8+6+4
0÷8+6+4
0+(8-6)×5
(0+8-6)×5
0+8-6+8
0×8+7+3
0÷8+7+3
0+8+7-5
0+8-7+9
0×8+8+2
0÷8+8+2
0+8+8÷4
0+8+8-6
0+8÷8+9
(0+8)÷8+9
0×8+9+1
0÷8+9+1
0-8+9×2
0+8+9-7
0-8+9+9
0+9+1+0
0+9+1-0
0+9+1×1
0+(9+1)×1
(0+9+1)×1
0+9+1÷1
0+(9+1)÷1
(0+9+1)÷1
0+9-1×1
0+9×1+1
(0+9)×1+1
0+9÷1+1
(0+9)÷1+1
0+9-1+2
0×9+1+9
0÷9+1+9
0+9+2-1
0+9+2÷2
0+9-2+3
0×9+2×5
(0×9+2)×5
0÷9+2×5
(0÷9+2)×5
0+9×2-8
(0+9)×2-8
0×9+2+8
0÷9+2+8
0+9+3-2
0+9+3÷3
0+9-3+4
0+9÷3+7
(0+9)÷3+7
0×9+3+7
0÷9+3+7
0+(9-4)×2
(0+9-4)×2
0+9+4-3
0+9+4÷4
0+9-4+5
0×9+4+6
0÷9+4+6
0×9+5×2
(0×9+5)×2
0÷9+5×2
(0÷9+5)×2
0+9+5-4
0+9+5÷5
0×9+5+5
0÷9+5+5
0+9-5+6
0×9+6+4
0÷9+6+4
0+9+6-5
0+9+6÷6
0+9-6+7
0×9+7+3
0÷9+7+3
0+(9-7)×5
(0+9-7)×5
0+9+7-6
0+9+7÷7
0+9-7+8
0×9+8+2
0÷9+8+2
0+9+8-7
0+9+8÷8
0+9-8+9
0×9+9+1
0÷9+9+1
0+9+9-8
0+9+9÷9
0+9÷9+9
(0+9)÷9+9
1+0+0+9
1+0-0+9
1+0×0+9
1-0+0+9
1-0-0+9
1-0×0+9 

1xxx

1000～1999

1+0+0+9
1+0-0+9
1+0×0+9
1-0+0+9
1-0-0+9
1-0×0+9
(1+0+1)×5
(1-0+1)×5
1+0+1+8
1-0+1+8
1+0+1×9
1+(0+1)×9
1+0-1×9
1+0×1+9
(1+0)×1+9
(1+0)×(1+9)
1+0÷1+9
(1+0)÷1+9
1-0+1×9
1-(0-1)×9
1-0×1+9
(1-0)×1+9
(1-0)×(1+9)
1-0÷1+9
(1-0)÷1+9
1×0+1+9
1×(0+1)+9
1×(0+1+9)
1÷(0+1)+9
(1+0)×2×5
(1-0)×2×5
1×0+2×5
1×(0+2)×5
1×(0+2×5)
(1×0+2)×5
1+0+2+7
1-0+2+7
(1+0)×2+8
(1+0)×(2+8)
(1-0)×2+8
(1-0)×(2+8)
1×0+2+8
1×(0+2)+8
1×(0+2+8)
1+0×2+9
1+0÷2+9
1-0×2+9
1-0÷2+9
1+0+3×3
1+(0+3)×3
1+0-3×3
1-0+3×3
1-(0-3)×3
1+0+3+6
1-0+3+6
(1+0)×3+7
(1+0)×(3+7)
(1-0)×3+7
(1-0)×(3+7)
1×0+3+7
1×(0+3)+7
1×(0+3+7)
1+0×3+9
1+0÷3+9
1-0×3+9
1-0÷3+9
(1+0+4)×2
(1-0+4)×2
1+0+4+5
1-0+4+5
(1+0)×4+6
(1+0)×(4+6)
(1-0)×4+6
(1-0)×(4+6)
1×0+4+6
1×(0+4)+6
1×(0+4+6)
1+0×4+9
1+0÷4+9
1-0×4+9
1-0÷4+9
(1+0)×5×2
(1-0)×5×2
1×0+5×2
1×(0+5)×2
1×(0+5×2)
(1×0+5)×2
1+0+5+4
1-0+5+4
(1+0)×5+5
(1+0)×(5+5)
(1-0)×5+5
(1-0)×(5+5)
1×0+5+5
1×(0+5)+5
1×(0+5+5)
1+0×5+9
1+0÷5+9
1-0×5+9
1-0÷5+9
1+0+6+3
1-0+6+3
(1+0)×6+4
(1+0)×(6+4)
(1-0)×6+4
(1-0)×(6+4)
1×0+6+4
1×(0+6)+4
1×(0+6+4)
1+0×6+9
1+0÷6+9
1-0×6+9
1-0÷6+9
1+0+7+2
1-0+7+2
(1+0)×7+3
(1+0)×(7+3)
(1-0)×7+3
(1-0)×(7+3)
1×0+7+3
1×(0+7)+3
1×(0+7+3)
1+0×7+9
1+0÷7+9
1-0×7+9
1-0÷7+9
1+0+8+1
1-0+8+1
(1+0)×8+2
(1+0)×(8+2)
(1-0)×8+2
(1-0)×(8+2)
1×0+8+2
1×(0+8)+2
1×(0+8+2)
1+0×8+9
1+0÷8+9
1-0×8+9
1-0÷8+9
1+0+9+0
1+0+9-0
1-0+9+0
1-9+9-0
1+0+9×1
1+(0+9)×1
(1+0+9)×1
1+0+9÷1
1+(0+9)÷1
(1+0+9)÷1
1+0-9×1
(1+0)×9+1
(1+0)×(9+1)
1-0+9×1
(1-0+9)×1
1-0+9÷1
1-(0-9)×1
1-(0-9)÷1
(1-0)×9+1
(1-0)×(9+1)
1-0×9÷1
1×0+9+1
1×(0+9)+1
1×(0+9+1)
1+0×9+9
1+0÷9+9
1-0×9+9
1-0÷9+9
(1+1)×(1+4)
(1+1)×1×5
(1+1×1)×5
(1+1)÷1×5
(1+1÷1)×5
1×(1+1)×5
(1×1+1)×5
(1÷1+1)×5
1+1+1+7
1+1+1×8
1+1-1×8
1+1×1+8
1+1×(1+8)
(1+1)×1+8
1+1÷1+8
(1+1)÷1+8
1×1+1+8
1×(1+1)+8
1×(1+1+8)
1÷1+1+8
1+1-1+9
1+1×1×9
1+1÷1×9
1-1+1+9
1×1+1×9
1×(1+1×9)
1×1×1+9
1×1×(1+9)
1×(1×1+9)
1×1÷1+9
1×(1÷1+9)
1÷1+1×9
1÷1×1+9
1÷1×(1+9)
1÷1÷1+9
1+(1+2)×3
(1+1)×(2+3)
1+1+2×4
1+1-2×4
1-1+2×5
(1-1+2)×5
1×1×2×5
1÷1×2×5
1+1+2+6
(1+1)×2+6
1+1×2+7
1+1×(2+7)
1×1+2+7
1×(1+2)+7
1×(1+2+7)
1÷1+2+7
1-1+2+8
1×1×2+8
1×1×(2+8)
1×(1×2+8)
1÷1×2+8
1÷1×(2+8)
(1+1)÷2+9
1-(1-2)×9
(1+1+3)×2
(1+1)×(3+2)
1+1×3×3
1×1+3×3
1×(1+3×3)
1÷1+3×3
(1+1)×3+4
1+1+3+5
1+1×3+6
1+1×(3+6)
1×1+3+6
1×(1+3)+6
1×(1+3+6)
1÷1+3+6
1-1+3+7
1×1×3+7
1×1×(3+7)
1×(1×3+7)
1÷1×3+7
1÷1×(3+7)
(1+1)×(4+1)
1+1+4×2
1+1-4×2
(1+1)×4+2
(1+1×4)×2
1×(1+4)×2
(1×1+4)×2
(1÷1+4)×2
1-(1-4)×3
1+1+4+4
1+1×4+5
1+1×(4+5)
1×1+4+5
1×(1+4)+5
1×(1+4+5)
1÷1+4+5
1-1+4+6
1×1×4+6
1×1×(4+6)
1×(1×4+6)
1÷1×4+6
1÷1×(4+6)
(1+1÷4)×8
(1+1)×5+0
(1+1)×(5+0)
(1+1)×5-0
(1+1)×(5-0)
(1+1)×5×1
(1+1)×5÷1
1-1+5×2
(1-1+5)×2
1×1×5×2
1÷1×5×2
1+1+5+3
1+1×5+4
1+1×(5+4)
1×1+5+4
1×(1+5)+4
1×(1+5+4)
1÷1+5+4
1-1+5+5
1×1×5+5
1×1×(5+5)
1×(1×5+5)
1÷1×5+5
1÷1×(5+5)
(1+1)×(6-1)
1+1+6+2
(1+1)×6-2
1+1×6+3
1+1×(6+3)
1×1+6+3
1×(1+6)+3
1×(1+6+3)
1÷1+6+3
1-1+6+4
1×1×6+4
1×1×(6+4)
1×(1×6+4)
1÷1×6+4
1÷1×(6+4)
1+1+7+1
1+1×7+2
1+1×(7+2)
(1+1)×(7-2)
1×1+7+2
1×(1+7)+2
1×(1+7+2)
1÷1+7+2
1-1+7+3
1×1×7+3
1×1×(7+3)
1×(1×7+3)
1÷1×7+3
1÷1×(7+3)
(1+1)×7-4
1+1+8+0
1+1+8-0
1+1+8×1
1+(1+8)×1
(1+1+8)×1
1+1+8÷1
1+(1+8)÷1
(1+1+8)÷1
1+1-8×1
1+1×8+1
1+1×(8+1)
1×1+8+1
1×(1+8)+1
1×(1+8+1)
1÷1+8+1
1-1+8+2
1×1×8+2
1×1×(8+2)
1×(1×8+2)
1÷1×8+2
1÷1×(8+2)
(1+1)×(8-3)
(1+1)×8-6
1+1×9+0
1+1×(9+0)
1+1×9-0
1+1×(9-0)
1×1+9+0
1×(1+9)+0
1×(1+9+0)
1×1+9-0
1×(1+9)-0
1×(1+9-0)
1÷1+9+0
1÷1+9-0
1+1+9-1
1+1×9×1
(1+1×9)×1
1+1×9÷1
(1+1×9)÷1
1-1+9+1
1×1+9×1
1×(1+9)×1
1×(1+9×1)
(1×1+9)×1
1×1+9÷1
1×(1+9)÷1
1×(1+9÷1)
(1×1+9)÷1
1×1×9+1
1×1×(9+1)
1×(1×9+1)
1÷1+9×1
(1÷1+9)×1
1÷1+9÷1
(1÷1+9)÷1
1÷1×9+1
1÷1×(9+1)
(1+1)×(9-4)
(1+1)×9-8
(1+1÷9)×9
1+(2+1)×3
1×2×(1+4)
(1+2-1)×5
1×2×1×5
1×2÷1×5
1+2+1+6
1+2+1×7
1+2-1×7
1+2×1+7
(1+2)×1+7
1+2÷1+7
(1+2)÷1+7
1×2+1+7
1×(2+1)+7
1×(2+1+7)
1+2-1+8
1×2+1×8
1×(2+1×8)
1×2×1+8
1×(2×1+8)
1×2÷1+8
1×(2÷1+8)
1+(2-1)×9
1×2-1+9
1×(2-1)+9
1×(2-1+9)
1÷(2-1)+9
(1+2+2)×2
(1+2×2)×2
1×2×(2+3)
(1+2)×2+4
1×2+2×4
1×(2+2×4)
(1÷2+2)×4
1+2+2+5
1+2×2+5
(1+2÷2)×5
1×2+2+6
1×(2+2)+6
1×(2+2+6)
1×2×2+6
1×(2×2+6)
1+2÷2+8
1+2-2+9
1+2÷2×9
1-2+2+9
1×2÷2+9
1×(2÷2+9)
1÷2×2+9
(1+2)×3+1
1×(2+3)×2
(1×2+3)×2
1×2×(3+2)
1+2×3+3
1+2+3+4
1×2×3+4
1×(2×3+4)
(1-2+3)×5
1×2+3+5
1×(2+3)+5
1×(2+3+5)
(1+2÷3)×6
1-2+3+8
(1+2)÷3+9
1-(2-3)×9
1+2×4+1
1×2×(4+1)
(1+2)×4-2
1×2+4×2
1×(2+4×2)
1×2×4+2
1×(2×4+2)
1+2+4+3
1×2+4+4
1×(2+4)+4
1×(2+4+4)
1÷2×4×5
1-2+4+7
1÷2×4+8
1×2×5+0
1×2×(5+0)
1×(2×5+0)
1×2×5-0
1×2×(5-0)
1×(2×5-0)
1+2×5-1
1×2×5×1
1×2×5÷1
1+2+5+2
1-(2-5)×3
1×2+5+3
1×(2+5)+3
1×(2+5+3)
1÷2×5×4
(1+2)×5-5
1-2+5+6
1+2+6+1
1×2×(6-1)
(1-2+6)×2
1×2+6+2
1×(2+6)+2
1×(2+6+2)
1×2×6-2
1×(2×6-2)
1+2×6-3
1-2+6+5
1÷2×6+7
(1+2)×6-8
1+2+7+0
1+2+7-0
1+2+7×1
1+(2+7)×1
(1+2+7)×1
1+2+7÷1
1+(2+7)÷1
(1+2+7)÷1
1+2-7×1
1×2+7+1
1×(2+7)+1
1×(2+7+1)
1×2×(7-2)
1-2+7+4
1×2×7-4
1×(2×7-4)
1+2×7-5
1×2+8+0
1×(2+8)+0
1×(2+8+0)
1×2+8-0
1×(2+8)-0
1×(2+8-0)
1+2+8-1
1×2+8×1
1×(2+8)×1
1×(2+8×1)
(1×2+8)×1
1×2+8÷1
1×(2+8)÷1
1×(2+8÷1)
(1×2+8)÷1
1-2+8+3
1×2×(8-3)
1×2×8-6
1×(2×8-6)
1÷2×8+6
1+2×8-7
(1+2÷8)×8
1×2+9-1
1×(2+9)-1
1×(2+9-1)
1+2+9-2
1+2×9÷2
1-2+9+2
1×2×(9-4)
1×2×9-8
1×(2×9-8)
1+2×9-9
(1+3+1)×2
1+3×(1+2)
1+3×1×3
1+3÷1×3
1-3×(1-4)
1+3+1+5
1×(3-1)×5
(1×3-1)×5
1+3+1×6
1+3-1×6
1+3×1+6
(1+3)×1+6
1+3÷1+6
(1+3)÷1+6
(1-3)×(1-6)
1×3+1+6
1×(3+1)+6
1×(3+1+6)
1+3-1+7
1×3+1×7
1×(3+1×7)
1×3×1+7
1×(3×1+7)
1×3÷1+7
1×(3÷1+7)
1×3-1+8
1×(3-1)+8
1×(3-1+8)
1+3×(2+1)
(1+3)×2+2
1×(3+2)×2
(1×3+2)×2
1+3+2×3
1+3-2×3
1+3×2+3
1+3+2+4
(1+3÷2)×4
1×3×2+4
1×(3×2+4)
(1+3-2)×5
(1+3)÷2×5
1-3×(2-5)
1×3+2+5
1×(3+2)+5
1×(3+2+5)
1+3÷2×6
1-3+2×6
(1-3)×(2-7)
1+3-2+8
(1+3)÷2+8
1+(3-2)×9
1×3-2+9
1×(3-2)+9
1×(3-2+9)
1÷(3-2)+9
1+3×3+0
1+3×(3+0)
1+3×3-0
1+3×(3-0)
1+3×3×1
(1+3×3)×1
1+3×3÷1
(1+3×3)÷1
1×3×3+1
1×(3×3+1)
1+3+3×2
1+3-3×2
(1+3)×3-2
1+3+3+3
(1÷3+3)×3
1-3+3×4
1×3+3+4
1×(3+3)+4
1×(3+3+4)
(1+3÷3)×5
1-3×(3-6)
1+3÷3+8
(1-3)×(3-8)
1+3-3+9
1+3÷3×9
1-3+3+9
1×3÷3+9
1×(3÷3+9)
1÷3×3+9
1+3×(4-1)
1+3+4+2
1×3×4-2
1×(3×4-2)
1+3×4-3
1-3+4×3
1×3+4+3
1×(3+4)+3
1×(3+4+3)
(1-3+4)×5
(1+3)×4-6
1-3×(4-7)
1-3+4+8
(1+3)÷4+9
1-(3-4)×9
(1-3)×(4-9)
1+3+5+1
1+3×(5-2)
(1+3)×5÷2
1×3+5+2
1×(3+5)+2
1×(3+5+2)
1×3×5-5
1×(3×5-5)
1+3×5-6
1÷3×5×6
1-3+5+7
1-3×(5-8)
1+3+6+0
1+3+6-0
1+3+6×1
1+(3+6)×1
(1+3+6)×1
1+3+6÷1
1+(3+6)÷1
(1+3+6)÷1
1+3-6×1
1×3+6+1
1×(3+6)+1
1×(3+6+1)
1+3×6÷2
1-3+6×2
1+3×(6-3)
1-(3-6)×3
1÷3×6×5
1-3+6+6
1×3×6-8
1×(3×6-8)
1÷3×6+8
1+3×6-9
1-3×(6-9)
1×3+7+0
1×(3+7)+0
1×(3+7+0)
1×3+7-0
1×(3+7)-0
1×(3+7-0)
1+3+7-1
1×3+7×1
1×(3+7)×1
1×(3+7×1)
(1×3+7)×1
1×3+7÷1
1×(3+7)÷1
1×(3+7÷1)
(1×3+7)÷1
(1-3+7)×2
1+3×(7-4)
1-3+7+5
(1+3÷7)×7
1×3+8-1
1×(3+8)-1
1×(3+8-1)
1+3+8-2
1-3+8+4
1+3×(8-5)
1×3+9-2
1×(3+9)-2
1×(3+9-2)
1+3+9-3
1+3×9÷3
1-3+9+3
1+3×(9-6)
1÷3×9+7
(1+4)×(1+1)
(1+4)×1×2
(1+4×1)×2
(1+4)÷1×2
(1+4÷1)×2
1×(4+1)×2
(1×4+1)×2
1+(4-1)×3
1+4+1+4
1+4+1×5
1+4-1×5
1+4×1+5
(1+4)×1+5
1+4÷1+5
(1+4)÷1+5
1×4+1+5
1×(4+1)+5
1×(4+1+5)
1+4-1+6
1×4+1×6
1×(4+1×6)
1×4×1+6
1×(4×1+6)
1×4÷1+6
1×(4÷1+6)
1×4-1+7
1×(4-1)+7
1×(4-1+7)
(1÷4+1)×8
(1+4)×2+0
(1+4)×(2+0)
(1+4)×2-0
(1+4)×(2-0)
1+4×2+1
(1+4)×2×1
(1+4)×2÷1
1×4×2+2
1×(4×2+2)
1+4+2+3
1×4+2×3
1×(4+2×3)
(1+4)÷2×4
1×4+2+4
1×(4+2)+4
1×(4+2+4)
1×(4-2)×5
(1×4-2)×5
1×4÷2×5
1+4-2+7
1+4÷2+7
1×4-2+8
1×(4-2)+8
1×(4-2+8)
1×4÷2+8
1×(4÷2+8)
(1+4)×(3-1)
1+4+3+2
1×4+3×2
1×(4+3×2)
1×4×3-2
1×(4×3-2)
1+4×3-3
1×4+3+3
1×(4+3)+3
1×(4+3+3)
(1+4-3)×5
(1+4)×3-5
(1+4)÷3×6
1+4-3+8
1+(4-3)×9
1×4-3+9
1×(4-3)+9
1×(4-3+9)
1÷(4-3)+9
1+4+4+1
(1+4)×(4-2)
(1+4)×4÷2
1×4+4+2
1×(4+4)+2
1×(4+4+2)
(1+4÷4)×5
1×4×4-6
1×(4×4-6)
1+4×4-7
1+4÷4+8
(1+4)÷4×8
1+4-4+9
1+4÷4×9
1-4+4+9
1×4÷4+9
1×(4÷4+9)
1÷4×4+9
1+4+5+0
1+4+5-0
1+4+5×1
1+(4+5)×1
(1+4+5)×1
1+4+5÷1
1+(4+5)÷1
(1+4+5)÷1
1+4-5×1
1×4+5+1
1×(4+5)+1
1×(4+5+1)
1×4×5÷2
(1+4)×(5-3)
(1-4+5)×5
1-4+5+8
1÷4×5×8
(1+4)÷5+9
1-(4-5)×9
1×4+6+0
1×(4+6)+0
1×(4+6+0)
1×4+6-0
1×(4+6)-0
1×(4+6-0)
1+4+6-1
1×4+6×1
1×(4+6)×1
1×(4+6×1)
(1×4+6)×1
1×4+6÷1
1×(4+6)÷1
1×(4+6÷1)
(1×4+6)÷1
(1+4)×6÷3
(1+4)×(6-4)
(1+4÷6)×6
1-4+6+7
1×4+7-1
1×(4+7)-1
1×(4+7-1)
1+4+7-2
1-(4-7)×3
(1+4)×(7-5)
1-4+7+6
(1-4+8)×2
1×4+8-2
1×(4+8)-2
1×(4+8-2)
1+4+8-3
(1+4)×8÷4
1-4+8+5
1÷4×8×5
(1+4)×(8-6)
1÷4×8+8
1×4+9-3
1×(4+9)-3
1×(4+9-3)
1+4+9-4
1+4×9÷4
1-4+9+4
(1+4)×(9-7)
1×5×(1+1)
(1+5-1)×2
1×5×1×2
1×5÷1×2
1+5+1+3
1+5+1×4
1+5-1×4
1+5×1+4
(1+5)×1+4
1+5÷1+4
(1+5)÷1+4
1×5+1+4
1×(5+1)+4
1×(5+1+4)
1+5-1+5
1×5+1×5
1×(5+1×5)
1×5×1+5
1×(5×1+5)
1×5÷1+5
1×(5÷1+5)
1×5-1+6
1×(5-1)+6
1×(5-1+6)
1×5×2+0
1×5×(2+0)
1×(5×2+0)
1×5×2-0
1×5×(2-0)
1×(5×2-0)
1+5×2-1
1×5×2×1
1×5×2÷1
1+5+2+2
1+5+2×2
1+5-2×2
(1+5)×2-2
1+(5-2)×3
1×5+2+3
1×(5+2)+3
1×(5+2+3)
1×5÷2×4
1+5-2+6
(1+5)÷2+7
1-5+2×7
1×5-2+7
1×(5-2)+7
1×(5-2+7)
1+5+3+1
1×5×(3-1)
1×5+3+2
1×(5+3)+2
1×(5+3+2)
(1+5)÷3×5
1×(5-3)×5
(1×5-3)×5
1×5×3-5
1×(5×3-5)
1+5×3-6
1×5÷3×6
1+5-3+7
(1+5)×3-8
(1+5)÷3+8
1×5-3+8
1×(5-3)+8
1×(5-3+8)
1+5+4+0
1+5+4-0
1+5+4×1
1+(5+4)×1
(1+5+4)×1
1+5+4÷1
1+(5+4)÷1
(1+5+4)÷1
1+5-4×1
1×5+4+1
1×(5+4)+1
1×(5+4+1)
1×5×(4-2)
1×5×4÷2
(1+5-4)×5
1+5-4+8
1×5÷4×8
1+(5-4)×9
1×5-4+9
1×(5-4)+9
1×(5-4+9)
1÷(5-4)+9
1×5+5+0
1×(5+5)+0
1×(5+5+0)
1×5+5-0
1×(5+5)-0
1×(5+5-0)
1+5+5-1
1×5+5×1
1×(5+5)×1
1×(5+5×1)
(1×5+5)×1
1×5+5÷1
1×(5+5)÷1
1×(5+5÷1)
(1×5+5)÷1
(1+5)×5÷3
1×5×(5-3)
(1+5÷5)×5
1+5÷5+8
1+5-5+9
1+5÷5×9
1-5+5+9
1×5÷5+9
1×(5÷5+9)
1÷5×5+9
1×5+6-1
1×(5+6)-1
1×(5+6-1)
1+5+6-2
1×5×6÷3
1×5×(6-4)
(1-5+6)×5
1-5+6+8
(1+5)÷6+9
1-(5-6)×9
1-5+7×2
1×5+7-2
1×(5+7)-2
1×(5+7-2)
1+5+7-3
1×5×(7-5)
1-5+7+7
1+5+8÷2
1-(5-8)×3
1×5+8-3
1×(5+8)-3
1×(5+8-3)
1+5+8-4
1×5×8÷4
1-5+8+6
1×5×(8-6)
(1-5+9)×2
1×5+9-4
1×(5+9)-4
1×(5+9-4)
1+5+9-5
1+5×9÷5
1-5+9+5
1×5×(9-7)
1+6+1+2
1×(6-1)×2
(1×6-1)×2
1+6+1×3
1+6-1×3
1+6×1+3
(1+6)×1+3
1+6÷1+3
(1+6)÷1+3
(1-6)×(1-3)
1×6+1+3
1×(6+1)+3
1×(6+1+3)
1+6-1+4
1×6+1×4
1×(6+1×4)
1×6×1+4
1×(6×1+4)
1×6÷1+4
1×(6÷1+4)
1×6-1+5
1×(6-1)+5
1×(6-1+5)
1+6+2+1
(1+6-2)×2
1×6+2+2
1×(6+2)+2
1×(6+2+2)
1×6+2×2
1×(6+2×2)
1×6×2-2
1×(6×2-2)
1+6×2-3
1+6÷2×3
(1+6)×2-4
(1-6)×(2-4)
1+6-2+5
1+6÷2+6
1×6-2+6
1×(6-2)+6
1×(6-2+6)
1×6÷2+7
1×(6÷2+7)
1+6+3+0
1+6+3-0
1+6+3×1
1+(6+3)×1
(1+6+3)×1
1+6+3÷1
1+(6+3)÷1
(1+6+3)÷1
1+6-3×1
1×6+3+1
1×(6+3)+1
1×(6+3+1)
1+6×3÷2
1+(6-3)×3
1-6+3×5
(1-6)×(3-5)
1×6÷3×5
1+6-3+6
1+6÷3+7
1×6-3+7
1×(6-3)+7
1×(6-3+7)
1×6×3-8
1×(6×3-8)
1×6÷3+8
1×(6÷3+8)
1+6×3-9
1×6+4+0
1×(6+4)+0
1×(6+4+0)
1×6+4-0
1×(6+4)-0
1×(6+4-0)
1+6+4-1
1×6+4×1
1×(6+4)×1
1×(6+4×1)
(1×6+4)×1
1×6+4÷1
1×(6+4)÷1
1×(6+4÷1)
(1×6+4)÷1
(1+6÷4)×4
1×(6-4)×5
(1×6-4)×5
1+6÷4×6
(1-6)×(4-6)
1+6-4+7
1×6-4+8
1×(6-4)+8
1×(6-4+8)
1×6+5-1
1×(6+5)-1
1×(6+5-1)
1+6+5-2
1-6+5×3
1×6×5÷3
(1+6-5)×5
(1-6)×(5-7)
1+6-5+8
1+(6-5)×9
1×6-5+9
1×(6-5)+9
1×(6-5+9)
1÷(6-5)+9
1+6+6÷2
1×6+6-2
1×(6+6)-2
1×(6+6-2)
1+6+6-3
1+6×6÷4
(1+6÷6)×5
1+6÷6+8
(1-6)×(6-8)
1+6-6+9
1+6÷6×9
1-6+6+9
1×6÷6+9
1×(6÷6+9)
1÷6×6+9
1×6+7-3
1×(6+7)-3
1×(6+7-3)
1+6+7-4
(1-6+7)×5
1-6+7+8
(1+6)÷7+9
1-(6-7)×9
(1-6)×(7-9)
1×6+8÷2
1×(6+8÷2)
1×6+8-4
1×(6+8)-4
1×(6+8-4)
1+6+8-5
1-6+8+7
1+6+9÷3
1-(6-9)×3
1×6+9-5
1×(6+9)-5
1×(6+9-5)
1+6+9-6
1+6×9÷6
(1+6÷9)×6
1-6+9+6
1+7+1+1
1+7+1×2
1+7-1×2
1+7×1+2
(1+7)×1+2
1+7÷1+2
(1+7)÷1+2
1×7+1+2
1×(7+1)+2
1×(7+1+2)
1+7-1+3
1×7+1×3
1×(7+1×3)
1×7×1+3
1×(7×1+3)
1×7÷1+3
1×(7÷1+3)
1×7-1+4
1×(7-1)+4
1×(7-1+4)
1+7+2+0
1+7+2-0
1+7+2×1
1+(7+2)×1
(1+7+2)×1
1+7+2÷1
1+(7+2)÷1
(1+7+2)÷1
1+7-2×1
1×7+2+1
1×(7+2)+1
1×(7+2+1)
1×(7-2)×2
(1×7-2)×2
1+7-2+4
1×7×2-4
1×(7×2-4)
1+7×2-5
1×7-2+5
1×(7-2)+5
1×(7-2+5)
(1+7)×2-6
(1+7)÷2+6
1-7+2×8
1×7+3+0
1×(7+3)+0
1×(7+3+0)
1×7+3-0
1×(7+3)-0
1×(7+3-0)
1+7+3-1
1×7+3×1
1×(7+3)×1
1×(7+3×1)
(1×7+3)×1
1×7+3÷1
1×(7+3)÷1
1×(7+3÷1)
(1×7+3)÷1
(1+7-3)×2
(1+7÷3)×3
1+7-3+5
1×7-3+6
1×(7-3)+6
1×(7-3+6)
1×7+4-1
1×(7+4)-1
1×(7+4-1)
1+7+4-2
1+7+4÷2
1+(7-4)×3
1-7+4×4
(1+7)÷4×5
1+7-4+6
1×7-4+7
1×(7-4)+7
1×(7-4+7)
(1+7)÷4+8
1×7+5-2
1×(7+5)-2
1×(7+5-2)
1+7+5-3
(1+7)×5÷4
1×(7-5)×5
(1×7-5)×5
1+7-5+7
1×7-5+8
1×(7-5)+8
1×(7-5+8)
1×7+6÷2
1×(7+6÷2)
1+7+6÷3
1×7+6-3
1×(7+6)-3
1×(7+6-3)
1+7+6-4
(1+7-6)×5
1+7-6+8
1+(7-6)×9
1×7-6+9
1×(7-6)+9
1×(7-6+9)
1÷(7-6)+9
1×7+7-4
1×(7+7)-4
1×(7+7-4)
1+7+7-5
(1+7×7)÷5
(1+7÷7)×5
1+7÷7+8
1+7-7+9
1+7÷7×9
1-7+7+9
1×7÷7+9
1×(7÷7+9)
1÷7×7+9
1-7+8×2
1+7+8÷4
(1-7+8)×5
1×7+8-5
1×(7+8)-5
1×(7+8-5)
1+7+8-6
1-7+8+8
(1+7)÷8+9
1-(7-8)×9
1×7+9÷3
1×(7+9÷3)
1×7+9-6
1×(7+9)-6
1×(7+9-6)
1+7+9-7
1+7×9÷7
1-7+9+7
1+8+1+0
1+8+1-0
1+8+1×1
1+(8+1)×1
(1+8+1)×1
1+8+1÷1
1+(8+1)÷1
(1+8+1)÷1
1+8-1×1
1+8×1+1
(1+8)×1+1
1+8÷1+1
(1+8)÷1+1
1×8+1+1
1×(8+1)+1
1×(8+1+1)
1+8-1+2
1×8+1×2
1×(8+1×2)
1×8×1+2
1×(8×1+2)
1×8÷1+2
1×(8÷1+2)
1×8-1+3
1×(8-1)+3
1×(8-1+3)
1×8+2+0
1×(8+2)+0
1×(8+2+0)
1×8+2-0
1×(8+2)-0
1×(8+2-0)
1+8+2-1
1×8+2×1
1×(8+2)×1
1×(8+2×1)
(1×8+2)×1
1×8+2÷1
1×(8+2)÷1
1×(8+2÷1)
(1×8+2)÷1
1+8+2÷2
(1+8÷2)×2
1+8-2+3
1×8-2+4
1×(8-2)+4
1×(8-2+4)
1+8÷2+5
1×8×2-6
1×(8×2-6)
1×8÷2+6
1×(8÷2+6)
1+8×2-7
(1+8)×2-8
1×8+3-1
1×(8+3)-1
1×(8+3-1)
1+8+3-2
1×(8-3)×2
(1×8-3)×2
1+8+3÷3
1+8-3+4
1×8-3+5
1×(8-3)+5
1×(8-3+5)
(1+8)÷3+7
(1+8-4)×2
1×8+4-2
1×(8+4)-2
1×(8+4-2)
1×8+4÷2
1×(8+4÷2)
1+8+4-3
1+8+4÷4
1+8-4+5
1×8÷4×5
1×8-4+6
1×(8-4)+6
1×(8-4+6)
1+8÷4+7
1×8÷4+8
1×(8÷4+8)
1+(8-5)×3
1×8+5-3
1×(8+5)-3
1×(8+5-3)
1+8+5-4
1×8×5÷4
1+8+5÷5
1+8-5+6
1×8-5+7
1×(8-5)+7
1×(8-5+7)
1×8+6÷3
1×(8+6÷3)
1×8+6-4
1×(8+6)-4
1×(8+6-4)
1+8+6-5
1×(8-6)×5
(1×8-6)×5
1+8+6÷6
1+8-6+7
1×8-6+8
1×(8-6)+8
1×(8-6+8)
(1+8-7)×5
1×8+7-5
1×(8+7)-5
1×(8+7-5)
1+8+7-6
1+8+7÷7
1+8-7+8
1+(8-7)×9
1×8-7+9
1×(8-7)+9
1×(8-7+9)
1÷(8-7)+9
1×8+8÷4
1×(8+8÷4)
(1+8÷8)×5
1×8+8-6
1×(8+8)-6
1×(8+8-6)
1+8+8-7
1+8+8÷8
1+8÷8+8
1+8-8+9
1+8÷8×9
1-8+8+9
1×8÷8+9
1×(8÷8+9)
1÷8×8+9
(1-8+9)×5
1×8+9-7
1×(8+9)-7
1×(8+9-7)
1+8+9-8
1+8×9÷8
1-8+9+8
1+8+9÷9
(1+8)÷9+9
1-(8-9)×9
1+9+1×0
1+9-1×0
1+9×1+0
1+9×(1+0)
(1+9)×1+0
(1+9)×(1+0)
1+9×1-0
1+9×(1-0)
(1+9)×1-0
(1+9)×(1-0)
1+9÷1+0
1+9÷(1+0)
(1+9)÷1+0
(1+9)÷(1+0)
1+9÷1-0
1+9÷(1-0)
(1+9)÷1-0
(1+9)÷(1-0)
1×9+1+0
1×(9+1)+0
1×(9+1+0)
1×9+1-0
1×(9+1)-0
1×(9+1-0)
1+9+1-1
1+9-1+1
1+9×1×1
(1+9)×1×1
(1+9×1)×1
1+9×1÷1
(1+9)×1÷1
(1+9×1)÷1
1+9÷1×1
(1+9)÷1×1
(1+9)÷(1×1)
(1+9÷1)×1
1+9÷1÷1
(1+9÷1)÷1
1×9+1×1
1×(9+1)×1
1×(9+1×1)
(1×9+1)×1
1×9+1÷1
1×(9+1)÷1
1×(9+1÷1)
(1×9+1)÷1
1×9×1+1
1×(9×1+1)
1×9÷1+1
1×(9÷1+1)
1-9×(1-2)
1-9÷(1-2)
1×9-1+2
1×(9-1)+2
1×(9-1+2)
(1÷9+1)×9
1+9+2×0
1+9-2×0
1+9×(2-1)
(1+9)×(2-1)
1+9÷(2-1)
(1+9)÷(2-1)
1×9+2-1
1×(9+2)-1
1×(9+2-1)
1+9+2-2
1+9-2+2
1+9×2÷2
(1+9)×2÷2
1+9÷2×2
(1+9)÷2×2
1×9+2÷2
1×(9+2÷2)
1-9×(2-3)
1-9÷(2-3)
1×9-2+3
1×(9-2)+3
1×(9-2+3)
(1+9)÷2+5
1×9×2-8
1×(9×2-8)
1+9×2-9
1-9+2×9
1+9+3×0
1+9-3×0
1+9×(3-2)
(1+9)×(3-2)
1+9÷(3-2)
(1+9)÷(3-2)
1×9+3-2
1×(9+3)-2
1×(9+3-2)
1+9+3-3
1+9-3+3
1+9×3÷3
(1+9)×3÷3
1+9÷3×3
(1+9)÷3×3
1×9+3÷3
1×(9+3÷3)
1-9×(3-4)
1-9÷(3-4)
1×9-3+4
1×(9-3)+4
1×(9-3+4)
1+9÷3+6
1-9+3×6
1×9÷3+7
1×(9÷3+7)
1+9+4×0
1+9-4×0
1×(9-4)×2
(1×9-4)×2
1+9×(4-3)
(1+9)×(4-3)
1+9÷(4-3)
(1+9)÷(4-3)
1×9+4-3
1×(9+4)-3
1×(9+4-3)
1+9+4-4
1+9-4+4
1+9×4÷4
(1+9)×4÷4
1+9÷4×4
(1+9)÷4×4
1×9+4÷4
1×(9+4÷4)
1-9×(4-5)
1-9÷(4-5)
1×9-4+5
1×(9-4)+5
1×(9-4+5)
1+9+5×0
1+9-5×0
(1+9-5)×2
1+9×(5-4)
(1+9)×(5-4)
1+9÷(5-4)
(1+9)÷(5-4)
1×9+5-4
1×(9+5)-4
1×(9+5-4)
1+9+5-5
1+9-5+5
1+9×5÷5
(1+9)×5÷5
1+9÷5×5
(1+9)÷5×5
1×9+5÷5
1×(9+5÷5)
1-9×(5-6)
1-9÷(5-6)
1×9-5+6
1×(9-5)+6
1×(9-5+6)
(1+9)÷5+8
1+9+6×0
1+9-6×0
1+(9-6)×3
1-9+6×3
(1+9÷6)×4
1+9×(6-5)
(1+9)×(6-5)
1+9÷(6-5)
(1+9)÷(6-5)
1×9+6-5
1×(9+6)-5
1×(9+6-5)
1+9+6-6
1+9-6+6
1+9×6÷6
(1+9)×6÷6
1+9÷6×6
(1+9)÷6×6
1×9+6÷6
1×(9+6÷6)
1-9×(6-7)
1-9÷(6-7)
1×9-6+7
1×(9-6)+7
1×(9-6+7)
1+9+7×0
1+9-7×0
1×(9-7)×5
(1×9-7)×5
1+9×(7-6)
(1+9)×(7-6)
1+9÷(7-6)
(1+9)÷(7-6)
1×9+7-6
1×(9+7)-6
1×(9+7-6)
1+9+7-7
1+9-7+7
1+9×7÷7
(1+9)×7÷7
1+9÷7×7
(1+9)÷7×7
1×9+7÷7
1×(9+7÷7)
1-9×(7-8)
1-9÷(7-8)
1×9-7+8
1×(9-7)+8
1×(9-7+8)
1+9+8×0
1+9-8×0
(1+9-8)×5
1+9×(8-7)
(1+9)×(8-7)
1+9÷(8-7)
(1+9)÷(8-7)
1×9+8-7
1×(9+8)-7
1×(9+8-7)
1+9+8-8
1+9-8+8
1+9×8÷8
(1+9)×8÷8
1+9÷8×8
(1+9)÷8×8
1×9+8÷8
1×(9+8÷8)
1+(9-8)×9
1-9×(8-9)
1-9÷(8-9)
1×9-8+9
1×(9-8)+9
1×(9-8+9)
1÷(9-8)+9
1+9+9×0
1+9-9×0
1+(9+9)÷2
1-9+9×2
(1+9÷9)×5
1+9×(9-8)
(1+9)×(9-8)
1+9÷9+8
1+9÷(9-8)
(1+9)÷(9-8)
1×9+9-8
1×(9+9)-8
1×(9+9-8)
1+9+9-9
1+9-9+9
1+9×9÷9
(1+9)×9÷9
1+9÷9×9
(1+9)÷9×9
1-9+9+9
1×9+9÷9
1×(9+9÷9)
1×9÷9+9
1×(9÷9+9)
1÷9×9+9

2xxx

2000～2999

(2+0+0)×5
(2+0-0)×5
(2+0)×(0+5)
(2+0×0)×5
(2-0+0)×5
(2-0-0)×5
(2-0)×(0+5)
(2-0×0)×5
2×(0+0+5)
2×(0-0+5)
2×(0×0+5)
2+0+0+8
2+0-0+8
2+0×0+8
2-0+0+8
2-0-0+8
2-0×0+8
(2+0)×(1+4)
(2-0)×(1+4)
2×(0+1+4)
(2+0)×1×5
(2+0×1)×5
(2+0)÷1×5
(2+0÷1)×5
(2-0)×1×5
(2-0×1)×5
(2-0)÷1×5
(2-0÷1)×5
2×(0+1)×5
2×(0+1×5)
2×(0×1+5)
2×(0÷1+5)
2÷(0+1)×5
2÷(0+1÷5)
2×(0-1+6)
2+0+1+7
2-0+1+7
2+0+1×8
2+(0+1)×8
2+0-1×8
2+0×1+8
(2+0)×1+8
2+0÷1+8
(2+0)÷1+8
2-0+1×8
2-(0-1)×8
2-0×1+8
(2-0)×1+8
2-0÷1+8
(2-0)÷1+8
2×(0+1)+8
2÷(0+1)+8
2+0-1+9
2-0-1+9
2×0+1+9
(2+0)×(2+3)
(2-0)×(2+3)
2×(0+2+3)
2+0+2×4
2+(0+2)×4
2+0-2×4
2-0+2×4
2-(0-2)×4
(2+0×2)×5
(2+0÷2)×5
(2-0×2)×5
(2-0÷2)×5
2×0+2×5
(2×0+2)×5
2×(0×2+5)
2×(0÷2+5)
2+0+2+6
(2+0)×2+6
2-0+2+6
(2-0)×2+6
2×(0+2)+6
2×(0-2+7)
2+0×2+8
2+0÷2+8
2-0×2+8
2-0÷2+8
2×0+2+8
(2+0)÷2+9
(2-0)÷2+9
2÷(0+2)+9
(2+0+3)×2
(2+0)×(3+2)
(2-0+3)×2
(2-0)×(3+2)
2×(0+3+2)
(2+0)×3+4
(2-0)×3+4
2×(0+3)+4
2+0+3+5
(2+0×3)×5
(2+0÷3)×5
2-0+3+5
(2-0×3)×5
(2-0÷3)×5
2×(0×3+5)
2×(0÷3+5)
2×0+3+7
2+0×3+8
2+0÷3+8
2-0×3+8
2-0÷3+8
2×(0-3+8)
(2+0)×(4+1)
(2-0)×(4+1)
2×(0+4+1)
2+0+4×2
2+(0+4)×2
2+0-4×2
(2+0)×4+2
2-0+4×2
2-(0-4)×2
(2-0)×4+2
2×(0+4)+2
2+0+4+4
2-0+4+4
(2+0×4)×5
(2+0÷4)×5
(2-0×4)×5
(2-0÷4)×5
2×(0×4+5)
2×(0÷4+5)
2×0+4+6
2+0×4+8
2+0÷4+8
2-0×4+8
2-0÷4+8
2×(0-4+9)
(2+0)×5+0
(2+0)×(5+0)
(2+0)×5-0
(2+0)×(5-0)
(2-0)×5+0
(2-0)×(5+0)
(2-0)×5-0
(2-0)×(5-0)
2×(0+5)+0
2×(0+5+0)
2×(0+5)-0
2×(0+5-0)
(2+0)×5×1
(2+0)×5÷1
(2-0)×5×1
(2-0)×5÷1
2×(0+5)×1
2×(0+5×1)
2×(0+5)÷1
2×(0+5÷1)
2×0+5×2
(2×0+5)×2
2+0+5+3
2-0+5+3
(2+0×5)×5
(2+0÷5)×5
(2-0×5)×5
(2-0÷5)×5
2×0+5+5
2×(0×5+5)
2×(0÷5+5)
2+0×5+8
2+0÷5+8
2-0×5+8
2-0÷5+8
(2+0)×(6-1)
(2-0)×(6-1)
2×(0+6-1)
2+0+6+2
(2+0)×6-2
2-0+6+2
(2-0)×6-2
2×(0+6)-2
2×0+6+4
(2+0×6)×5
(2+0÷6)×5
(2-0×6)×5
(2-0÷6)×5
2×(0×6+5)
2×(0÷6+5)
2+0×6+8
2+0÷6+8
2-0×6+8
2-0÷6+8
2+0+7+1
2-0+7+1
(2+0)×(7-2)
(2-0)×(7-2)
2×(0+7-2)
2×0+7+3
(2+0)×7-4
(2-0)×7-4
2×(0+7)-4
(2+0×7)×5
(2+0÷7)×5
(2-0×7)×5
(2-0÷7)×5
2×(0×7+5)
2×(0÷7+5)
2+0×7+8
2+0÷7+8
2-0×7+8
2-0÷7+8
2+0+8+0
2+0+8-0
2-0+8+0
2-8+8-0
2+0+8×1
2+(0+8)×1
(2+0+8)×1
2+0+8÷1
2+(0+8)÷1
(2+0+8)÷1
2+0-8×1
2-0+8×1
(2-0+8)×1
2-0+8÷1
2-(0-8)×1
2-(0-8)÷1
2-0×8÷1
2×0+8+2
(2+0)×(8-3)
(2-0)×(8-3)
2×(0+8-3)
(2+0×8)×5
(2+0÷8)×5
(2-0×8)×5
(2-0÷8)×5
2×(0×8+5)
2×(0÷8+5)
(2+0)×8-6
(2-0)×8-6
2×(0+8)-6
2+0×8+8
2+0÷8+8
2-0×8+8
2-0÷8+8
2+0+9-1
2-9+9-1
2×0+9+1
(2+0)×(9-4)
(2-0)×(9-4)
2×(0+9-4)
(2+0×9)×5
(2+0÷9)×5
(2-0×9)×5
(2-0÷9)×5
2×(0×9+5)
2×(0÷9+5)
2+0×9+8
(2+0)×9-8
2+0÷9+8
2-0×9+8
(2-0)×9-8
2-0÷9+8
2×(0+9)-8
2×(1+1+3)
2+(1+1)×4
2×(1+1×4)
2×1×(1+4)
2×(1×1+4)
2×(1÷1+4)
2÷1×(1+4)
(2+1-1)×5
(2-1+1)×5
2×(1-1+5)
2×1×1×5
2×1÷1×5
2÷1×1×5
2÷1÷1×5
2+1+1+6
2×(1+1)+6
2+1+1×7
2+1-1×7
2+1×1+7
2+1×(1+7)
(2+1)×1+7
2+1÷1+7
(2+1)÷1+7
2×1+1+7
2÷1+1+7
2+1-1+8
2+1×1×8
2+1÷1×8
2-1+1+8
2×1+1×8
2×1×1+8
2×1÷1+8
2÷1+1×8
2÷1×1+8
2÷1÷1+8
2-1+1×9
2-1×1+9
(2-1)×1+9
(2-1)×(1+9)
2-1×(1-9)
2-1÷1+9
(2-1)÷1+9
2×1-1+9
2÷(1+1)+9
2÷1-1+9
(2+1+2)×2
2×(1+2+2)
2×(1+2×2)
2×1×(2+3)
2×(1×2+3)
2÷1×(2+3)
(2+1)×2+4
2+1×2×4
(2+1÷2)×4
2×(1+2)+4
2×1+2×4
2÷1+2×4
2+1+2+5
(2-1)×2×5
2+1×2+6
2+1×(2+6)
2×1+2+6
2×(1-2+6)
2×1×2+6
2÷1+2+6
2÷1×2+6
2-1+2+7
2-(1-2)×8
(2-1)×2+8
(2-1)×(2+8)
2+1-2+9
2×1÷2+9
2÷1÷2+9
(2+1)×3+1
2×(1+3+1)
2+(1+3)×2
(2+1×3)×2
2×(1+3)+2
(2×1+3)×2
2×1×(3+2)
2×(1×3+2)
(2÷1+3)×2
2÷1×(3+2)
2-1+3×3
2+1+3+4
2-(1-3)×4
2×1×3+4
2÷1×3+4
2+1×3+5
2+1×(3+5)
2×1+3+5
2÷1+3+5
2-1+3+6
(2-1÷3)×6
(2-1)×3+7
(2-1)×(3+7)
2×(1-3+7)
(2+1)÷3+9
2×(1+4)+0
2×(1+4+0)
2×(1+4)-0
2×(1+4-0)
2×(1+4)×1
2×(1+4×1)
2×(1+4)÷1
2×(1+4÷1)
2×1×(4+1)
2×(1×4+1)
2÷1×(4+1)
(2+1)×4-2
2+1×4×2
(2-1+4)×2
2×1+4×2
2×1×4+2
2÷1+4×2
2÷1×4+2
2+1+4+3
2+1×4+4
2+1×(4+4)
2×1+4+4
2÷1+4+4
2-1+4+5
2÷(1-4÷5)
(2-1)×4+6
(2-1)×(4+6)
2×(1-4+8)
2×1×5+0
2×1×(5+0)
2×(1×5+0)
2×1×5-0
2×1×(5-0)
2×(1×5-0)
2÷1×5+0
2÷1×(5+0)
2÷1×5-0
2÷1×(5-0)
2÷(1÷5+0)
2÷(1÷5-0)
2×(1+5-1)
2×1×5×1
2×1×5÷1
2÷1×5×1
2÷1×5÷1
2+1+5+2
2-(1-5)×2
(2-1)×5×2
2×(1+5)-2
2+1×5+3
2+1×(5+3)
2×1+5+3
2÷1+5+3
2-1+5+4
(2+1)×5-5
(2-1)×5+5
(2-1)×(5+5)
2×(1-5+9)
2+1+6+1
2×1×(6-1)
2×(1×6-1)
2÷1×(6-1)
2+1×6+2
2+1×(6+2)
2×1+6+2
2×(1+6-2)
2×1×6-2
2÷1+6+2
2÷1×6-2
2-1+6+3
(2-1)×6+4
(2-1)×(6+4)
2×(1+6)-4
(2+1)×6-8
2+1+7+0
2+1+7-0
2+1+7×1
2+(1+7)×1
(2+1+7)×1
2+1+7÷1
2+(1+7)÷1
(2+1+7)÷1
2+1-7×1
2+1×7+1
2+1×(7+1)
2×1+7+1
2÷1+7+1
2-1+7+2
2×1×(7-2)
2×(1×7-2)
2÷1×(7-2)
(2-1)×7+3
(2-1)×(7+3)
2×(1+7-3)
2×1×7-4
2÷1×7-4
2×(1+7)-6
2+1×8+0
2+1×(8+0)
2+1×8-0
2+1×(8-0)
2×1+8+0
2×1+8-0
2÷1+8+0
2÷1+8-0
2+1+8-1
2+1×8×1
(2+1×8)×1
2+1×8÷1
(2+1×8)÷1
2-1+8+1
2×1+8×1
(2×1+8)×1
2×1+8÷1
(2×1+8)÷1
2÷1+8×1
(2÷1+8)×1
2÷1+8÷1
(2÷1+8)÷1
(2-1)×8+2
(2-1)×(8+2)
2×(1+8÷2)
2×1×(8-3)
2×(1×8-3)
2÷1×(8-3)
2×(1+8-4)
2×1×8-6
2÷1×8-6
2×(1+8)-8
2-1+9+0
2-9+9-0
2+1×9-1
2+1×(9-1)
2-1+9×1
(2-1+9)×1
2-1+9÷1
2-(1-9)×1
2-(1-9)÷1
(2-1)×9+1
(2-1)×(9+1)
2-1×9÷1
2×1+9-1
2÷1+9-1
2+1+9-2
2×(1+9)÷2
2×1×(9-4)
2×(1×9-4)
2÷1×(9-4)
2×(1+9-5)
2×1×9-8
2÷1×9-8
(2+2+1)×2
2×(2+1+2)
(2×2+1)×2
2+2×(1+3)
2×(2+1×3)
2×(2×1+3)
2×(2÷1+3)
2+2×1×4
2+2÷1×4
2×(2+1)+4
2×(2-1+4)
2+2+1+5
2-2×(1-5)
2×2+1+5
2×(2-1)×5
(2÷2+1)×5
2÷(2-1)×5
2+2+1×6
2+2-1×6
2+2×1+6
(2+2)×1+6
2+2÷1+6
(2+2)÷1+6
2×2+1×6
2×2×1+6
2×2÷1+6
2+2-1+7
2×2-1+7
2+(2-1)×8
2×(2-1)+8
2÷2+1+8
2÷(2-1)+8
2-2+1+9
2÷2+1×9
2÷2×1+9
2÷2×(1+9)
2÷2÷1+9
2×(2+2+1)
2×(2×2+1)
2+(2+2)×2
2+2×(2+2)
(2+2)×2+2
2+2×2×2
2×(2+2)+2
2×2×2+2
2+2+2×3
2+2-2×3
2×2+2×3
2+2+2+4
2+2×2+4
2×2+2+4
2×(2÷2+4)
(2+2-2)×5
(2+2)÷2×5
2-2+2×5
(2-2+2)×5
2×(2-2+5)
(2×2-2)×5
2×2÷2×5
2÷2×2×5
2-2×(2-6)
2+2÷2+7
2÷2+2+7
2+2-2+8
(2+2)÷2+8
2+2÷2×8
2-2+2+8
2×2-2+8
2×2÷2+8
2÷2×2+8
2÷2×(2+8)
2-2÷2+9
2×(2+3)+0
2×(2+3+0)
2×(2+3)-0
2×(2+3-0)
2+2×(3+1)
2×(2+3)×1
2×(2+3×1)
2×(2+3)÷1
2×(2+3÷1)
2×(2×3-1)
2+2+3×2
2+2-3×2
2+2×3+2
(2+2)×3-2
2×2+3×2
2×2×3-2
2+2+3+3
2×2+3+3
2÷2+3×3
2×(2-3+6)
2÷2+3+6
2-2+3+7
2-2×(3-7)
2÷2×3+7
2÷2×(3+7)
2-(2-3)×8
2+2-3+9
2×2-3+9
2+2×4+0
2+2×(4+0)
2+2×4-0
2+2×(4-0)
2+2×4×1
(2+2×4)×1
2+2×4÷1
(2+2×4)÷1
2×(2+4-1)
2+2+4+2
2×2+4+2
2×(2+4)-2
(2÷2+4)×2
2×(2×4-3)
(2+2÷4)×4
2-(2-4)×4
2÷2+4+5
(2+2)×4-6
2-2+4+6
2×2×4-6
2÷2×4+6
2÷2×(4+6)
2×(2-4+7)
2-2×(4-8)
(2+2)÷4+9
2×2÷4+9
2+2+5+1
2+2×(5-1)
2×2+5+1
2+2×5-2
(2+2)×5÷2
2-2+5×2
(2-2+5)×2
2×(2+5-2)
2×2×5÷2
2÷2×5×2
2×(2+5)-4
2÷2+5+4
2-2+5+5
2×(2×5-5)
2÷2×5+5
2÷2×(5+5)
2×(2-5+8)
2-2×(5-9)
2+2+6+0
2+2+6-0
2×2+6+0
2×2+6-0
2+2+6×1
2+(2+6)×1
(2+2+6)×1
2+2+6÷1
2+(2+6)÷1
(2+2+6)÷1
2+2-6×1
2×2+6×1
(2×2+6)×1
2×2+6÷1
(2×2+6)÷1
2+2×(6-2)
2-(2-6)×2
2×(2+6÷2)
2×(2+6-3)
2÷2+6+3
2+2×6-4
2-2+6+4
2÷2×6+4
2÷2×(6+4)
(2-2÷6)×6
2×(2+6)-6
2×(2×6-7)
2×(2-6+9)
2+2+7-1
2×2+7-1
2÷2+7+2
2+2×(7-3)
2-2+7+3
2÷2×7+3
2÷2×(7+3)
2×(2+7-4)
2+2×7-6
2×(2+7)-8
2×(2×7-9)
2÷2+8+1
2+2+8-2
2+2×8÷2
2-2+8+2
2×2+8-2
2×(2+8)÷2
2÷2×8+2
2÷2×(8+2)
2+2×(8-4)
2×(2+8-5)
2+2×8-8
2÷2+9+0
2÷2+9-0
2-2+9+1
2÷2+9×1
(2÷2+9)×1
2÷2+9÷1
(2÷2+9)÷1
2÷2×9+1
2÷2×(9+1)
(2+2×9)÷2
2+2+9-3
2×2+9-3
2×(2+9÷3)
2+2×(9-5)
2÷(2-9÷5)
2×(2+9-6)
(2+3)×(1+1)
2×(3+1+1)
2+(3+1)×2
(2+3)×1×2
(2+3×1)×2
(2+3)÷1×2
(2+3÷1)×2
2×(3+1)+2
2×(3+1×2)
(2×3-1)×2
2×(3×1+2)
2×(3÷1+2)
2×3+1+3
2×(3-1+3)
2+3+1+4
2+(3-1)×4
2×3+1×4
2×3×1+4
2×3÷1+4
2+3+1×5
2+3-1×5
2+3×1+5
(2+3)×1+5
2+3÷1+5
(2+3)÷1+5
2×3-1+5
2+3-1+6
2×(3-1)+6
(2÷3+1)×6
2÷(3-1)+9
(2+3)×2+0
(2+3)×(2+0)
(2+3)×2-0
(2+3)×(2-0)
2×(3+2)+0
2×(3+2+0)
2×(3+2)-0
2×(3+2-0)
(2+3)×2×1
(2+3)×2÷1
2×(3+2)×1
2×(3+2×1)
2×(3+2)÷1
2×(3+2÷1)
2×(3×2-1)
2+3×2+2
2×3+2+2
2×3+2×2
2×3×2-2
2+3+2+3
(2+3)÷2×4
2×(3-2+4)
2×(3-2)×5
2÷(3-2)×5
2×3-2+6
2+3-2+7
2×3÷2+7
2+(3-2)×8
2×(3-2)+8
2÷(3-2)+8
2-3+2+9
2+3×3-1
(2+3)×(3-1)
2×3+3+1
2×(3+3-1)
2+3+3+2
2×(3+3)-2
2×(3×3-4)
2×(3÷3+4)
(2+3-3)×5
(2+3)×3-5
(2-3+3)×5
2×(3-3+5)
2×3÷3×5
2÷3×3×5
(2+3)÷3×6
2+3÷3+7
2×3-3+7
2+3-3+8
2+3÷3×8
2-3+3+8
2×3×3-8
2×3÷3+8
2÷3×3+8
2-3÷3+9
2×3+4+0
2×3+4-0
2+3+4+1
2×3+4×1
(2×3+4)×1
2×3+4÷1
(2×3+4)÷1
(2+3)×(4-2)
(2+3)×4÷2
2×(3+4-2)
2×(3+4÷2)
2+3×4-4
2×(3+4)-4
(2×3-4)×5
2×(3-4+6)
2-3+4+7
2×(3×4-7)
(2+3)÷4×8
2-(3-4)×8
(2-3÷4)×8
2×3-4+8
2+3-4+9
2+3+5+0
2+3+5-0
2+3+5×1
2+(3+5)×1
(2+3+5)×1
2+3+5÷1
2+(3+5)÷1
(2+3+5)÷1
2+3-5×1
2×3+5-1
(2+3)×(5-3)
2×(3+5-3)
2×3×5÷3
2÷3×5×3
2-(3-5)×4
2-3+5+6
2×(3+5)-6
2+3×5-7
2×(3-5+7)
(2+3)÷5+9
2×3-5+9
2+3+6-1
(2+3×6)÷2
(2-3+6)×2
2×3+6-2
(2+3)×6÷3
2×(3+6÷3)
(2+3)×(6-4)
(2+3÷6)×4
2×(3+6-4)
2-3+6+5
2÷3×6+6
2×(3+6)-8
2×(3-6+8)
2×3÷6+9
2÷3×(6+9)
2+3+7-2
2-(3-7)×2
2×(3+7)÷2
2×3+7-3
2-3+7+4
(2+3)×(7-5)
2×(3+7-5)
2÷3×(7+8)
2×(3-7+9)
2×3+8÷2
2+3+8-3
2+3×8÷3
2-3+8+3
(2+3)×8÷4
2×3+8-4
2×(3+8÷4)
(2+3)×(8-6)
2×(3+8-6)
2÷3×(8+7)
2-3+9+2
2+3+9-4
2÷3×9+4
2×3+9-5
(2-3÷9)×6
2÷3×(9+6)
(2+3)×(9-7)
2×(3+9-7)
2×(4+1)+0
2×(4+1+0)
2×(4+1)-0
2×(4+1-0)
2+4×(1+1)
2×4+1+1
2×(4+1)×1
2×(4+1×1)
2×(4+1)÷1
2×(4+1÷1)
2×(4×1+1)
2×(4÷1+1)
(2+4-1)×2
2+4×1×2
2+4÷1×2
2×4+1×2
2×(4-1+2)
2×4×1+2
2×4÷1+2
2+4+1+3
2-4×(1-3)
2×4-1+3
2+4+1×4
2+4-1×4
2+4×1+4
(2+4)×1+4
2+4÷1+4
(2+4)÷1+4
2×(4-1)+4
2+4-1+5
(2-4)×(1-6)
2+4×2+0
2+4×(2+0)
2+4×2-0
2+4×(2-0)
2×4+2+0
2×4+2-0
2+4×2×1
(2+4×2)×1
2+4×2÷1
(2+4×2)÷1
2×(4+2-1)
2×4+2×1
(2×4+2)×1
2×4+2÷1
(2×4+2)÷1
2+4+2+2
2+4+2×2
2+4-2×2
(2+4)×2-2
2×(4+2)-2
2×(4+2÷2)
2×(4-2+3)
2×(4×2-3)
2×(4÷2+3)
2+(4-2)×4
2+4÷2×4
2-4×(2-4)
2×4-2+4
(2÷4+2)×4
2+4-2+6
2+4÷2+6
2-4+2×6
2×(4-2)+6
2×4×2-6
2×4÷2+6
(2+4)÷2+7
(2-4)×(2-7)
2÷(4-2)+9
2÷4×2+9
2+4+3+1
2+4×(3-1)
2×4+3-1
2×(4+3-2)
(2×4-3)×2
(2+4÷3)×3
2×(4+3÷3)
2+4×3-4
2-4+3×4
2×(4+3)-4
2×(4-3+4)
(2+4)÷3×5
2-4×(3-5)
2×4-3+5
2×(4-3)×5
2÷(4-3)×5
2+4÷3×6
2+4-3+7
2×(4×3-7)
2+(4-3)×8
(2+4)×3-8
(2+4)÷3+8
(2-4)×(3-8)
2×(4-3)+8
2÷(4-3)+8
2-4+3+9
2+4+4+0
2+4+4-0
2+4+4×1
2+(4+4)×1
(2+4+4)×1
2+4+4÷1
2+(4+4)÷1
(2+4+4)÷1
2+4-4×1
2+4×(4-2)
2+4×4÷2
2×4+4-2
2×4+4÷2
2-4+4×3
2×(4+4-3)
2×(4+4÷4)
2×(4÷4+4)
(2+4-4)×5
(2-4+4)×5
2×(4-4+5)
2×4÷4×5
2÷4×4×5
2-4×(4-6)
2×(4+4)-6
2×4-4+6
2+4÷4+7
2+4-4+8
2+4×4-8
2+4÷4×8
2-4+4+8
2×4÷4+8
2÷4×4+8
(2-4)×(4-9)
2-4÷4+9
2+4+5-1
2+4×(5-3)
(2+4)×5÷3
2×4+5-3
2×(4+5-4)
2×4×5÷4
2÷4×5×4
2×(4+5÷5)
2×(4-5+6)
2-4+5+7
2-4×(5-7)
2×4-5+7
2-(4-5)×8
2×(4+5)-8
2+4-5+9
2+4+6-2
2-4+6×2
2×(4+6)÷2
2+4×6÷3
2×4+6÷3
2+4×(6-4)
2-(4-6)×4
2×4+6-4
2×(4+6-5)
(2×4-6)×5
2-4+6+6
2×(4+6÷6)
2×(4-6+7)
2÷4×6+7
2-4×(6-8)
2×4-6+8
(2+4)÷6+9
(2-4+7)×2
2+4+7-3
(2+4×7)÷3
2+4×(7-5)
2-4+7+5
2×4+7-5
2×(4+7-6)
(2-4÷7)×7
2×(4+7÷7)
2×(4-7+8)
2-4×(7-9)
2×4-7+9
2+4+8÷2
2-(4-8)×2
2+4+8-4
2+4×8÷4
(2+4÷8)×4
2-4+8+4
2×4+8÷4
2+4×(8-6)
2×4+8-6
2÷4×8+6
2×(4+8-7)
2×(4+8÷8)
2×(4-8+9)
2×4÷8+9
2-4+9+3
2+4+9-5
2+4×(9-7)
2×4+9-7
2×(4+9-8)
2×(4+9÷9)
2×5+1×0
2×(5+1×0)
2×5-1×0
2×(5-1×0)
2×5×1+0
2×5×(1+0)
2×(5×1+0)
2×5×1-0
2×5×(1-0)
2×(5×1-0)
2×5÷1+0
2×5÷(1+0)
2×(5÷1+0)
2×5÷1-0
2×5÷(1-0)
2×5+1-1
2×(5+1-1)
2×5-1+1
2×(5-1+1)
2×5×1×1
2×5×1÷1
2×5÷1×1
2×5÷1÷1
2+5+1+2
2+(5-1)×2
2×(5+1)-2
2×(5-1)+2
2+5+1×3
2+5-1×3
2+5×1+3
(2+5)×1+3
2+5÷1+3
(2+5)÷1+3
2+5-1+4
2×5+2×0
2×(5+2×0)
2×5-2×0
2×(5-2×0)
2+5+2+1
2×5×(2-1)
2×5÷(2-1)
(2+5-2)×2
2+5×2-2
2×5+2-2
2×(5+2-2)
2×5-2+2
2×(5-2+2)
2×5×2÷2
2×5÷2×2
(2+5)×2-4
2×(5+2)-4
2×(5-2)+4
2+5-2+5
2×(5×2-5)
2×5÷2+5
2+5+3+0
2+5+3-0
2×5+3×0
2×(5+3×0)
2×5-3×0
2×(5-3×0)
2+5+3×1
2+(5+3)×1
(2+5+3)×1
2+5+3÷1
2+(5+3)÷1
(2+5+3)÷1
2+5-3×1
2×5×(3-2)
2×5÷(3-2)
2×5+3-3
2×(5+3-3)
2×5-3+3
2×(5-3+3)
2×5×3÷3
2×5÷3×3
2+(5-3)×4
2+5-3+6
2×(5+3)-6
2×(5-3)+6
2+5×3-7
2÷(5-3)+9
2×5+4×0
2×(5+4×0)
2×5-4×0
2×(5-4×0)
2+5+4-1
2×5×(4-3)
2×5÷(4-3)
2×5+4-4
2×(5+4-4)
2×5-4+4
2×(5-4+4)
2×5×4÷4
2×5÷4×4
2×(5-4)×5
2÷(5-4)×5
2+5-4+7
2+(5-4)×8
2×(5+4)-8
2×(5-4)+8
2÷(5-4)+8
2-5+4+9
2×5+5×0
2×(5+5×0)
2×5-5×0
2×(5-5×0)
2+5+5-2
2×(5+5)÷2
(2×5-5)×2
2×5×(5-4)
2×(5÷5+4)
2×5÷(5-4)
(2+5-5)×5
(2-5+5)×5
2×5+5-5
2×(5+5-5)
2×5-5+5
2×(5-5+5)
2×5×5÷5
2×5÷5×5
2÷5×5×5
2+5÷5+7
2+5-5+8
2+5÷5×8
2-5+5+8
2×5÷5+8
2÷5×5+8
2-5÷5+9
2×5+6×0
2×(5+6×0)
2×5-6×0
2×(5-6×0)
2+5+6÷2
2+5+6-3
2×5×(6-5)
2×5÷(6-5)
2×5+6-6
2×(5+6-6)
2×5-6+6
2×(5-6+6)
2×5×6÷6
2×5÷6×6
2-5+6+7
2-(5-6)×8
2+5-6+9
2×5+7×0
2×(5+7×0)
2×5-7×0
2×(5-7×0)
2+5+7-4
2-(5-7)×4
2-5+7+6
2×5×(7-6)
2×5÷(7-6)
2×5+7-7
2×(5+7-7)
2×5-7+7
2×(5-7+7)
2×5×7÷7
2×5÷7×7
(2+5)÷7+9
2×5+8×0
2×(5+8×0)
2×5-8×0
2×(5-8×0)
(2-5+8)×2
2+5+8-5
2+5×8÷5
2-5+8+5
(2×5-8)×5
2×5×(8-7)
2×5÷(8-7)
2×5+8-8
2×(5+8-8)
2×5-8+8
2×(5-8+8)
2×5×8÷8
2×5÷8×8
2×5+9×0
2×(5+9×0)
2×5-9×0
2×(5-9×0)
2-(5-9)×2
2+5+9÷3
2-5+9+4
2+5+9-6
2×5×(9-8)
2×5÷(9-8)
2×5+9-9
2×(5+9-9)
2×5-9+9
2×(5-9+9)
2×5×9÷9
2×5÷9×9
2×(6-1)+0
2×(6-1+0)
2×(6-1)-0
2×(6-1-0)
2+6+1+1
2×6-1-1
2×(6-1)×1
2×(6-1×1)
2×(6-1)÷1
2×(6-1÷1)
2×(6×1-1)
2+6+1×2
2+6-1×2
2+6×1+2
(2+6)×1+2
2+6÷1+2
(2+6)÷1+2
2×(6+1-2)
2×6-1×2
2×6×1-2
2×6÷1-2
2+6-1+3
2×6+1-3
2×(6+1)-4
2+6+2+0
2+6+2-0
2×6-2+0
2×6-2-0
2+6+2×1
2+(6+2)×1
(2+6+2)×1
2+6+2÷1
2+(6+2)÷1
(2+6+2)÷1
2+6-2×1
2+(6-2)÷1
2×(6-2+1)
2×6-2×1
(2×6-2)×1
2×6-2÷1
2+(6-2)×2
(2+6÷2)×2
2×(6-2)+2
2×(6-2÷2)
2×(6÷2+2)
2×(6+2-3)
2+6-2+4
2+6×2-4
2×6+2-4
2×6÷2+4
2+6÷2+5
(2+6)×2-6
(2+6)÷2+6
2×(6+2)-6
2-6+2×7
2×(6×2-7)
2+6+3-1
2×6-3+1
(2+6-3)×2
(2+6×3)÷2
2×(6-3+2)
2×(6-3÷3)
2×(6÷3+3)
(2÷6+3)×3
2+6÷3×4
2×(6+3-4)
2×(6-3)+4
2+6-3+5
2×6+3-5
2+6÷3+6
2×6÷3+6
2×(6+3)-8
2÷6×3+9
2+6+4-2
2+6+4÷2
2×(6+4)÷2
2×6-4+2
2×6-4÷2
2+6×4÷3
2×(6-4+3)
2+(6-4)×4
2×(6-4÷4)
(2+6)÷4×5
2×(6+4-5)
2+6-4+6
2×6+4-6
2×(6-4)+6
2×6÷4+7
(2+6)÷4+8
2÷(6-4)+9
2÷(6÷5-1)
2+6+5-3
2×6-5+3
(2+6)×5÷4
2×(6-5+4)
2×(6-5)×5
2×(6-5÷5)
2÷(6-5)×5
2×(6+5-6)
2×6×5÷6
2÷6×5×6
2+6-5+7
2×6+5-7
2+(6-5)×8
2×(6-5)+8
2÷(6-5)+8
2-6+5+9
2+6+6÷3
2×6-6÷3
2+6+6-4
2×6-6+4
2×(6÷6+4)
(2+6-6)×5
(2-6+6)×5
2×(6-6+5)
2×6÷6×5
2÷6×6×5
2×(6-6÷6)
2+6÷6+7
2×(6+6-7)
2+6-6+8
2+6÷6×8
2-6+6+8
2×6+6-8
2×6÷6+8
2÷6×6+8
2-6÷6+9
2-6+7×2
(2×6-7)×2
2+6+7-5
2×6-7+5
2×(6-7+6)
2-6+7+7
2×(6-7÷7)
2-(6-7)×8
2×(6+7-8)
2+6-7+9
2×6+7-9
(2×6+8)÷2
2+6+8÷4
2-(6-8)×4
2×6-8÷4
(2+6×8)÷5
2+6+8-6
2+6×8÷6
2-6+8+6
2×6-8+6
2×(6-8+7)
(2-6÷8)×8
2×(6-8÷8)
(2+6)÷8+9
2×(6+8-9)
(2-6+9)×2
2×(6+9)÷3
2-6+9+5
2+6+9-7
2×6-9+7
2÷6×9+7
2×(6-9+8)
2×(6-9÷9)
2+7+1+0
2+7+1-0
2+7+1×1
2+(7+1)×1
(2+7+1)×1
2+7+1÷1
2+(7+1)÷1
(2+7+1)÷1
2+7-1×1
2+7×1+1
(2+7)×1+1
2+7÷1+1
(2+7)÷1+1
2×(7-1-1)
2+7-1+2
2×(7-1)-2
2×(7-1×2)
2×(7×1-2)
(2-7)×(1-3)
2×(7+1-3)
2×7-1-3
2×7-1×4
2×7×1-4
2×7÷1-4
2×7+1-5
2×(7+1)-6
2×(7-2)+0
2×(7-2+0)
2×(7-2)-0
2×(7-2-0)
2+7+2-1
2×(7-2)×1
2×(7-2×1)
2×(7-2)÷1
2×(7-2÷1)
2+7+2÷2
2×7-2-2
2×7-2×2
2+7-2+3
2×7÷2+3
(2-7)×(2-4)
2×(7+2-4)
2+7×2-6
2×7+2-6
(2+7)×2-8
2×(7+2)-8
2×(7×2-9)
2×(7-3+1)
2×7-3-1
2+7+3-2
2+(7-3)×2
2×(7+3)÷2
2×(7-3)+2
2+7+3÷3
2+7-3+4
2-7+3×5
(2-7)×(3-5)
2×(7+3-5)
(2+7)÷3+7
2×7+3-7
2×7-4+0
2×7-4-0
2+(7-4)÷1
2×7-4×1
(2×7-4)×1
2×7-4÷1
(2+7-4)×2
2×(7-4+2)
2×(7-4÷2)
2+7+4-3
(2+7×4)÷3
2+7+4÷4
2×(7-4)+4
2+7-4+5
(2-7)×(4-6)
2×(7+4-6)
2×7+4-8
2×7-5+1
2-7+5×3
2×(7-5+3)
2+7+5-4
2+(7-5)×4
2+7+5÷5
2+7-5+6
2×(7-5)+6
(2-7)×(5-7)
2×(7+5-7)
2×7×5÷7
2÷7×5×7
2×7+5-9
2÷(7-5)+9
(2×7+6)÷2
2×7-6+2
2×(7-6÷3)
2×(7-6+4)
2+7+6-5
2×(7-6)×5
2÷(7-6)×5
2+7+6÷6
2+7-6+7
2+(7-6)×8
(2-7)×(6-8)
2×(7+6-8)
2×(7-6)+8
2÷(7-6)+8
2-7+6+9
2×7-7+3
2×(7÷7+4)
(2+7-7)×5
(2-7+7)×5
2×(7-7+5)
2×7÷7×5
2÷7×7×5
2+7+7-6
2+7+7÷7
2+7÷7+7
2+7-7+8
2+7÷7×8
2-7+7+8
2×7÷7+8
2÷7×7+8
(2-7)×(7-9)
2-7÷7+9
2×(7+7-9)
2×7-8÷2
2×(7+8)÷3
2×7-8+4
2×(7-8÷4)
2×(7-8+6)
2+7+8-7
2+7×8÷7
2-7+8+7
2+7+8÷8
2-(7-8)×8
2+7-8+9
2+(7+9)÷2
(2×7-9)×2
2-(7-9)×4
2×7-9+5
2-7+9+6
2×(7-9+7)
2+7+9-8
2+7+9÷9
(2+7)÷9+9
2+8+1×0
2+8-1×0
2+8×1+0
2+8×(1+0)
(2+8)×1+0
(2+8)×(1+0)
2+8×1-0
2+8×(1-0)
(2+8)×1-0
(2+8)×(1-0)
2+8÷1+0
2+8÷(1+0)
(2+8)÷1+0
(2+8)÷(1+0)
2+8÷1-0
2+8÷(1-0)
(2+8)÷1-0
(2+8)÷(1-0)
2+8+1-1
2+8-1+1
2+8×1×1
(2+8)×1×1
(2+8×1)×1
2+8×1÷1
(2+8)×1÷1
(2+8×1)÷1
2+8÷1×1
(2+8)÷1×1
(2+8)÷(1×1)
(2+8÷1)×1
2+8÷1÷1
(2+8÷1)÷1
2-8×(1-2)
2-8÷(1-2)
2×(8-1-2)
2×(8-1×3)
2×(8×1-3)
2×(8+1-4)
2×(8-1)-4
2×8-1-5
2×8-1×6
2×8×1-6
2×8÷1-6
2×8+1-7
2×(8+1)-8
(2÷8+1)×8
2+8+2×0
2+8-2×0
2+8×(2-1)
(2+8)×(2-1)
2+8÷(2-1)
(2+8)÷(2-1)
2×(8-2-1)
2×(8÷2+1)
2+8+2-2
2+8-2+2
2+8×2÷2
(2+8)×2÷2
2+8÷2×2
(2+8)÷2×2
2×(8+2)÷2
2×(8-2)-2
2×8÷2+2
2-8×(2-3)
2-8÷(2-3)
2×8-2×3
2+8÷2+4
2×8-2-4
(2+8)÷2+5
2×(8+2-5)
2+8×2-8
2-8+2×8
2×8+2-8
2+8+3×0
2+8-3×0
2×(8-3)+0
2×(8-3+0)
2×(8-3)-0
2×(8-3-0)
2×(8-3)×1
2×(8-3×1)
2×(8-3)÷1
2×(8-3÷1)
2+8×(3-2)
(2+8)×(3-2)
2+8÷(3-2)
(2+8)÷(3-2)
2×8-3×2
2+8+3-3
2+8-3+3
2+8×3÷3
(2+8)×3÷3
2+8÷3×3
(2+8)÷3×3
2×8-3-3
2-8×(3-4)
2-8÷(3-4)
2×(8+3-6)
2×8+3-9
2+8+4×0
2+8-4×0
2×(8-4+1)
2+(8-4)×2
(2×8+4)÷2
2×(8-4)+2
2×8-4-2
2+8×(4-3)
(2+8)×(4-3)
2+8÷(4-3)
(2+8)÷(4-3)
2×(8÷4+3)
2+8+4-4
2+8-4+4
2+8×4÷4
(2+8)×4÷4
2+8÷4×4
(2+8)÷4×4
2-8+4×4
2-8×(4-5)
2-8÷(4-5)
2+8÷4+6
2×8÷4+6
2×(8+4-7)
2÷8×4+9
2+8+5×0
2+8-5×0
2×8-5-1
(2+8-5)×2
2×(8-5+2)
2+8×(5-4)
(2+8)×(5-4)
2+8÷(5-4)
(2+8)÷(5-4)
2×(8-5)+4
2+8+5-5
2+8-5+5
2+8×5÷5
(2+8)×5÷5
2+8÷5×5
(2+8)÷5×5
2-8×(5-6)
2-8÷(5-6)
(2+8)÷5+8
2×(8+5-8)
2×8×5÷8
2÷8×5×8
2+8+6×0
2+8-6×0
2×8-6+0
2×8-6-0
2+(8-6)÷1
2×8-6×1
(2×8-6)×1
2×8-6÷1
2×(8-6÷2)
(2+8÷6)×3
2×(8-6+3)
2+(8-6)×4
2+8×(6-5)
(2+8)×(6-5)
(2+8×6)÷5
2+8÷(6-5)
(2+8)÷(6-5)
2+8+6-6
2+8-6+6
2+8×6÷6
(2+8)×6÷6
2+8÷6×6
(2+8)÷6×6
2×(8-6)+6
2-8×(6-7)
2-8÷(6-7)
2×(8+6-9)
2÷(8-6)+9
2+8+7×0
2+8-7×0
2×8-7+1
2×(8+7)÷3
2×(8-7+4)
2×(8-7)×5
2÷(8-7)×5
2+8×(7-6)
(2+8)×(7-6)
2+8÷(7-6)
(2+8)÷(7-6)
2+8+7-7
2+8-7+7
2+8×7÷7
(2+8)×7÷7
2+8÷7×7
(2+8)÷7×7
2+(8-7)×8
2-8×(7-8)
2-8÷(7-8)
2×(8-7)+8
2÷(8-7)+8
2-8+7+9
2+8+8×0
2+8-8×0
2+(8+8)÷2
2-8+8×2
2×8-8+2
2×(8÷8+4)
(2+8-8)×5
(2-8+8)×5
2×(8-8+5)
2×8÷8×5
2÷8×8×5
2+8×(8-7)
(2+8)×(8-7)
2+8÷8+7
2+8÷(8-7)
(2+8)÷(8-7)
2+8+8-8
2+8-8+8
2+8×8÷8
(2+8)×8÷8
2+8÷8×8
(2+8)÷8×8
2-8+8+8
2×8÷8+8
2÷8×8+8
2-8×(8-9)
2-8÷8+9
2-8÷(8-9)
2+8+9×0
2+8-9×0
2×8-9+3
2×(8-9÷3)
2×(8-9+6)
2-8+9+7
2+8×(9-8)
(2+8)×(9-8)
2+8÷(9-8)
(2+8)÷(9-8)
2-(8-9)×8
2+8+9-9
2+8-9+9
2+8×9÷9
(2+8)×9÷9
2+8÷9×9
(2+8)÷9×9
(2-8÷9)×9
2+9-1+0
2+9-1-0
2+(9-1)×1
(2+9-1)×1
2+9-1÷1
(2+9-1)÷1
2+9×1-1
(2+9)×1-1
2+9÷1-1
(2+9)÷1-1
2+9+1-2
2×(9+1)÷2
2×(9-1-3)
2×(9-1×4)
2×(9×1-4)
2×(9+1-5)
2×(9-1)-6
2×9-1-7
2×9-1×8
2×9×1-8
2×9÷1-8
2×9+1-9
2+9-2+1
2×9÷2+1
2+9-2÷2
(2+9×2)÷2
(2×9+2)÷2
2×(9-2-2)
2×(9-2×2)
2+9+2-3
2×(9-2)-4
2×9-2×4
2×(9+2-6)
2×9-2-6
2×(9-3-1)
2+9-3+2
(2+9÷3)×2
2×(9-3)-2
2×(9÷3+2)
2+9-3÷3
2+9+3-4
2×9÷3+4
2+9÷3+5
2×9-3-5
2×(9+3-7)
2×(9-4)+0
2×(9-4+0)
2×(9-4)-0
2×(9-4-0)
2×(9-4)×1
2×(9-4×1)
2×(9-4)÷1
2×(9-4÷1)
2×9-4×2
2+9-4+3
2+9-4÷4
2×9-4-4
2+9+4-5
2×(9+4-8)
2×(9-5+1)
2+(9-5)×2
2×(9-5)+2
2×9-5-3
2+9-5+4
2+9-5÷5
2+9+5-6
2×(9+5-9)
2×9×5÷9
2÷9×5×9
(2+9-6)×2
2×(9-6+2)
2×9-6-2
2×(9+6)÷3
2×(9-6)+4
2+9-6+5
2+9-6÷6
2+9+6-7
2×9÷6+7
2×9-7-1
2+(9+7)÷2
2×(9-7+3)
2+(9-7)×4
2+9-7+6
2×(9-7)+6
2+9-7÷7
2+9+7-8
2÷(9-7)+9
2×9-8+0
2×9-8-0
2+(9-8)÷1
2×9-8×1
(2×9-8)×1
2×9-8÷1
2×(9-8÷2)
2×(9-8+4)
2×(9-8)×5
2÷(9-8)×5
2+9-8+7
2+(9-8)×8
2+9-8÷8
2×(9-8)+8
2÷(9-8)+8
2+9+8-9
2+9×8÷9
2-9+8+9
2×9-9+1
(2+9+9)÷2
2×(9÷9+4)
(2+9-9)×5
(2-9+9)×5
2×(9-9+5)
2×9÷9×5
2÷9×9×5
2+9÷9+7
2+9-9+8
2+9÷9×8
2-9+9+8
2×9÷9+8
2÷9×9+8
2+9-9÷9
2-9÷9+9

3xxx～

　ブログの文字数制限により, これ以降は別ページになります.

blog.thetheorier.com

blog.thetheorier.com

blog.thetheorier.com

「最近台風多くない？」は正しいのか

　台風に限らず, 毎年…のように定期的に起こることに対してこのように思うことはよくあります, 気温もそうですね.

　実際のところどうなのか, 実際に調べてみました.

スポンサーリンク

---

過去68年の記録をグラフに

気象庁｜台風の統計資料

このページは、統計を開始した1951年以降に発生した台風に関する様々な統計資料を掲載しています。

　グラフの作成にあたり, 各種データは気象庁が発表したものを利用しています.

発生数

　まずは実際に太平洋上に発生した台風の数(累積)です.

　なおこの数はその年の1月から12月に発生した月別数としてカウントされています.

　画像の通り, 日本に来るかはさておき1月でも発生する年は普通にあります.

　9月を最後に一度も発生しない年もあれば12月いっぱいまで発生する年もあるようです.

　統計が行われた51年以降で年間発生数が一番多いのは1967年の39個, 一番少ない年は2010年の14個です.

　1951年から2017年までの平均は約26個のようです.

　上はゴチャゴチャしているので過去10年(2008年以降)に減らしてみました.

　1951年以降のものと比べると最終的な発生数は低めであることがわかります.

 　因みに新潟・福井豪雨があった2004年は発生数29と, 数としては統計上は中程度であることになります.

　発生数と個々の台風の威力が大して相関しないのは言うまでもありません.

　年ごとの発生数のグラフです.

　こうしてみると51年以降での評価としては露骨な発生数の上下は見られず, 強いて挙げるなら1960～70年辺りでピークがあるように見えます.

接近数

　発生した台風の中には日本に向かわないものもあります.

　なので今度は日本に接近した台風の数を見てみます.

　当然ですが発生数と比べてその数は減り, 接近数が増え始めるのが概ね4月になってからの年が多くなります.

　また6～9月での増加が発生数のグラフより顕著に見られるようになりました.

　最も多い年が1966年と2004年で14個, 最も少ないのは1973年で4個でした.

　平均すると約12個ですね.

　年間数のグラフに直すと全体的に露骨は傾向はあまり見られません.

　局地的に見れば1960年台までに一つの山, そして2004年, 2012年が印象的です.

　当時に年間20個もの接近があった年が1960年台にもあったんですね.

　このグラフが1970年から始まっていたら一次近似することで増加傾向があると評価するでしょう.

上陸数

　最後は実際に日本のどこかに上陸した数です.

　概ね6個以下に収まっていますが一つだけ, 2004年が際立っていますね.

　逆に一度も上陸しなかった年は

1984年, 1986年, 2000年, 2008年

の4つです.

　平均して年間約2.9個の台風が日本に上陸しています, 接近・上陸する台風の規模にもよりますが, 概ね3個は上陸してるんですね.

　なお統計上では7月時点での上陸数は約0.69個, 8月では一気に約1.72個となります.

　8月までには1個は上陸するような台風が来る可能性は十分あるということですね.

　年別の上陸数です.

　1985年前後を底に一度減少し, 以降は平均の倍以上の台風が上陸する年が頻繁に起こっているとわかります.

〆

　発生数や接近数を見るに, 「最近台風増えた」といった印象はあまり見られません.

　しかし上陸数を見ると90年以降の増加が気になります.

　この増加に至る理由はその年ごとの気候変動に大きく左右され, エルニーニョ・ラニーニャ現象, そしてモンスーンなどに影響してその進路や規模, 寿命が変わります.

　従って上記のような過去の発生数等だけで評価できるものではとてもじゃないですがありません.

　とはいえ「最近台風が増えた」という程度を説明するには十分でしょう, 最近増えたかどうか過去との比較で説明できるからです.

【数学】合同式の基本性質

　高校数学で合同式が採用されましたが, まだまだ「余り」から脱却できない節があります.

スポンサーリンク

---

合同式の基本性質

　と言うわけで今回は合同式で成り立つ性質を, 証明も合わせて見ていきたいと思います.

　その前に合同式の定義をおさらいしましょう.

[定義:合同式]

　整数 の差 が(一般に) より大きい整数 の倍数であるとき,

と書き表して「 は法 に関して合同」と言う.

　「余り」でも構いませんがそれだと例えば などを説明できないことは当ブログでも何度も指摘した通りです.

　折角合同式として習う以上, 「余り」に執着し過ぎず素直に従いましょう.

　というわけでここでは定義に, またその時点で証明済みの事実に基づいて結論を得ることを目的とします.

　なお, 断りの無い限り法は より大きい整数 とします.

　また一般的な整数(整域)は既知とします.

反射律

[証明]

　よって合同式の定義より

　上記から, 「 の倍数」は嫌でも認めなければならないこともわかります.

対称律

[証明]

　仮定より, ある整数 を用いて

が成り立つので, 変形して

, よって合同式の定義より

推移律

[証明]

　仮定より, ある整数 を用いて

が成り立つので, 2辺を足し合わせて整理すると

　よって は の倍数なので合同式の定義より

加法

[証明]

　仮定より, ある整数 が存在して

が成り立ちます.

　2式を足し合わせて整理すると

, つまり と の差が の倍数になります.

　よって合同式の定義より

加法可換

[証明]

なので, 合同式の定義より

加法単位元(零元)

　単位元とは, ここでは任意の整数 について

を満たす, (法 において)ただ一つの整数を指します.

[証明]

　先程加法可換であることは証明したので例えば について考えれば十分です.

　合同式の定義よりこれはある整数 が存在して

が成り立つことを意味します.

　整理すると

ですから は の倍数ということです.

　なので剰余類を代表して例えば として構いません(厳密には の倍数なら何でも良いので ).

　よって合同式の加法単位元は になります.

乗法

[証明]

　仮定より, ある整数 が存在して

が成り立ちます, これより

, よって は の倍数なので定義より

乗法可換

[証明]

なので, 合同式の定義より

乗法単位元

　ここでの単位元とは, 任意の整数 について

を満たす, (法 において)ただ一つの整数を指します.

[証明]

　先程乗法可換であることは証明したので例えば について考えれば十分です.

　合同式の定義よりこれはある整数 が存在して

が成り立つことを意味します.

　整理すると

, つまり または の少なくとも一方は の倍数です.

　なので剰余類を代表して例えば として構いません(厳密には の倍数なら何でも良いので ).

　加法可換の際は大して気にする必要はありませんでしたが, 単位元は「任意の元 について」ただ一つ存在しますので, 例えば がたまたま の倍数であったとしても関係ありません.

　従ってここでは が の倍数である必要があり, 代表して となります.

除法(簡約)

　 でない整数 について

のとき, ならば

, なる が存在するならば, なる整数 について

が成り立つ.

[証明]

　仮定より, ある整数 が存在して

, つまり は の倍数です.

( のとき)

　このとき は の倍数となりえないため が の倍数となります.

　よって合同式の定義より

( のとき)

　 と置くことで となります.

　このとき は , 即ち は の倍数となるのでやはり合同式の定義より

指数

　正整数 について,

[証明]

　数学的帰納法を利用します.

　 のときは自明なので省略.

　 のとき成り立つと仮定すると, 合同式の定義よりある整数 が存在して

が成り立ちます.

　下は変形して ですね, よって

と, が の倍数になるので定義より .

　従って数学的帰納法より証明されました.

〆

　このように, 通常の四則演算などと同じケースと違うケースが存在します.

blog.thetheorier.com

　対数に相当する指数は原始根を含め更に多くの文字数を要するので, 過去の記事を参考にしてください.

【数学】因数分解できるとは

　数学において因数分解は基本的であり, かつ重要な考え方の一つですね.

スポンサーリンク

---

因数分解とは

　その前に因数分解から復習しましょう.

　ひとまず数を対象とする集まりで考えます, 具体的には整数 の でない元 に対して

となる整数 が存在するとき, は因数 で因数分解できると言い, はどちらも と言います.

　特に ないし が素数であるとき, 特別に「素因数」と言い, 任意の正整数は然るべき素因数の積と等しいです, これを「素因数分解」と言います.

多項式の因数分解

　因数分解は何も数に限ったものではありません.

　例えば多項式でも同様に因数分解の考えができます.

　多項式 について,

を満たす整式 が存在するとき, は で因数分解できると言います.

　但し数の因数分解とは違って話は単純ではありません.

　例えば を因数分解するとしましょう, このときあなたは

で完結するでしょうか？それとも

とするでしょうか？

　このままではとちらもある意味で正解です, 問題は実数や複素数等, どの範囲で因数分解するべきかの違いです.

　後者は虚数である が含まれているため, 例えば「実数の範囲で」因数分解する場合 はこれ以上因数分解できないのです.

　一般に多項式 は, 最大次数の係数を無視すれば という形の一次多項式 個の積で表されます.

　このとき がどこまで許せるか…で, 因数分解可能な項が変化します, それを考慮すれば 次多項式は「高々」 個の多項式の積で表せることになります.

　従って単に「〜を因数分解してください」では解答が一通りになるとは限りません.

複素整数

　高校までで学ぶ範囲ではありませんが数の概念の一つとして「複素整数」があります.

　有理整数とは整数のことですが, 初等整数論においてこのように呼ぶことがあります.

　有理整数 と複素単位 について, 次の数を複素整数, もしくはガウス整数と言います.

　つまり実部虚部ともに整数である複素数をこのように呼ぶわけですね.

　複素整数は整数 を真に含む環であるため, とくに「ガウス整数環」ともとも言います.

　整数と似た性質を持ち, 例えば除法の定理

( はノルムと言い, 複素数の絶対値と同じ定義です )

が成り立ちます(但し一意性はありません).

　また素数に相当する概念もあります.

　複素整数のうち の つを「単数」と言い, 互いに単数による違いしか無い つの複素整数を「同伴」と言うのですが, 単数および 以外の複素整数 が単数および同伴数の他に約数を持たないとき, は「有理素数」と言います.

　これが整数(自然数)の素数に当たります.

　例えば は素数ですが, とできるため有理素数ではありません.

　整数(自然数)の世界では因数分解できない数が, 複素整数の世界だと因数分解できてしまうのですね.

【数学】平方根の定義

　よく言われるのが例えば

• は ? ?
• の平方根は ? ?

ですね.

スポンサーリンク

---

平方根とは

　平方根はしばしば以下のように定義されています.

[定義1:平方根]

　正実数 について, 乗して になる数を 「 の平方根」と言い, と書き表す.

　しかしよくよく考えてみれば も 乗して になりますからこれもまた「 の平方根」と考えることができます.

　「数」は等式関係を除いてただ一通りであることが大前提ですから, これは正しいようで定義がよろしくありません.

　その意味でも は正しくありません.

　従ってしばしば以下のようにも定義されます.

[定義2:平方根]

　正実数 について, 乗して になる数のうち正であるものを 「 の平方根」と言い, と書き表す.

　「らしく書く」ならこれは

を満たす正実数

ですね.

　これなら は除外されます.

n乗根

　平方根は上の通りで良さそうです, ではより一般的に 乗根についてはどうしましょう？

　一般の複素変数 の 次方程式

　 ( は正実数)

の解は, ド・モアブルにより以下となります.

　ようは複素数の範囲では 個の解を持ちます.

　この 個の複素数は定義から 乗して になる数です.

　従って が大きくなれば 乗根の候補もどんどん増えます.

　従って以下のように定義することになります.

[定義3: 乗根]

　任意の正実数 について,

を の 乗根と言う.

nが奇数のとき

　そもそも という数は, が奇数のとき 乗すると になってしまいます.

　そう言う意味では定義2の「正であるもの」も弱い定義と言えるかもしれません.

　存在しないことが明らかのため寧ろ都合が良いとも取れますけどね.

〆

　ただ説明するだけなら「 乗根とは のこと」と言ってしまえば楽ですが, 相手次第では例えばまだ複素数について習っていなかったりしますからね.

【数学】割った余りによる分類

　この考え方は合同式に絡みこれまでにも触れてきましたが, 本題に沿って改めて紹介しましょう.

スポンサーリンク

---

除法の定理

　本題のカギは除法の定理になります.

[定理：除法の定理]

　整数 について,

を満たす整数の組 がただ一組存在する.

　除法の定理の言わんとする点は, と との関係は勿論のこと, 任意の は 個の

という形で表すことができることを意味しています.

　つまり任意の整数 は

の何れかで表すことができる, 言いかえれば「分類できる」ことになります.

　通常はこれで問題ありません, しかし表記の仕方はこれだけなのでしょうか？

証明にヒントが

　そのカギは除法の定理の証明法の一つの内容にあります.

　 の倍数を小さい順に並べると

　 …(1)

となります.

　任意の整数 は上で並べた隣り合う特定の2数の間に必ず存在しますね, つまりある整数 が存在して

を満たします.

　除法の定理はここから「余り」に相当する数 を指定しますね.

少し変える

　任意の数 は何も の倍数である必要はありません.

　これを等間隔にズラしたものでも構いません, 従って例えば(1)から整数 だけズラした

　…(2)

と の関係を考えても良いはずです.

　この(2)を用いれば, 任意の は(2)による隣り合う2数の間に必ず存在します, つまりある整数 が存在して

を満たします, よって

と を置けば は であり, 上は変形して

となります.

　 は任意でしたから, を表す 個の列

は各々を同じ数で足し引きしても問題ないことになります.

　例えば整数 は整数 を用いて

の何れかで表すことができますが, 例えばこの各々を 引いた

でもやはり任意の整数を表すのです.

【数学】個人の得点と平均だけで偏差値を求めることはできるのか

　学生だったら気になる偏差値の話です.

スポンサーリンク

---

偏差値とは

　偏差値とは, ある標本が有限個のサンプルの中でどの位置にあるかを数値化したもので, 特に

• 平均値が 
• 標準偏差が 

となるようにしたものです.

　具体的な計算式は以下となっています.

[定義：偏差値]

• 個々人の点数：　(  ：標本数)
• 平均：
• 標準偏差：

と定めると, 個々人の偏差値 は以下となる.

　おおまかに, 平均点を取った人が  に, そしてもし得点分布が正規分布に近い場合, 例えば偏差値  以上が全体の約  となります.

　偏差値の理屈は各々の教科ごとの分布を統一するために一度標準化を行い, 更に平均値を取った人が偏差値  となるように調節したものになります.

個人の点数と平均だけでは計算できない

　この「標準偏差」が曲者で, 見ての通り個々の点数からなる分散を計算し, その平方根をとっています.

　従って素直に考えると自身の点数と, 全体の平均点数から自分の偏差値を求めるのは不可能です.

　流石にみんなの点数を聞いて回れるはずもありませんし.

　因みに最初に書いた「平均  , 標準偏差 」とは理論値のことを言ってますから, 実際のその試験の標準偏差が  になるということではありません.

おおよそなら分かる(かも)

　その代わり, その試験結果が正規分布に近いという仮定のもとであれば標準偏差はおおよそ決まってくるため自分の得点と平均だけでおよその偏差値が分かるかもしれません.

　というのももし標本が正規分布に従っているなら, 偏差値の理屈により標準偏差が  であろうことになるからです.

　実際の得点から計算するしかないのは変わりませんが, 正規分布に近い結果であれば概ね  辺りと思われます.

　従って「点数がピッタリ正規分布に従っている」という条件下では, 偏差値は以下となります.

　「自分自身を平均で引いて  を足す」ということですね, ピッタリ平均の人を考えればごく自然に見えます.

〆

　現実にはなかなかそう簡単には計算できません.

　人数が少なければちょっとした違いで大きくズレますし.