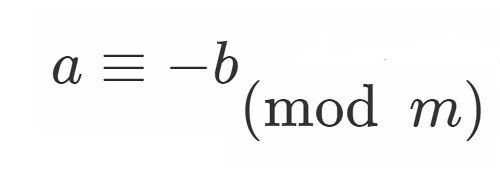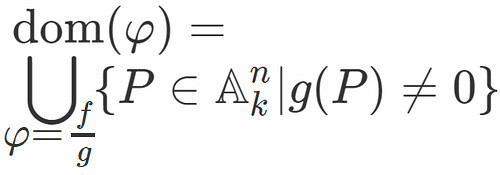
現在人が扱っている数は, それまで認められなかったものを含んでいます.
過去現在当たり前に使っている  や負数, 実数などは「あり得ない」とされてきた地域・過去があります.
や負数, 実数などは「あり得ない」とされてきた地域・過去があります.
スポンサーリンク
「数と量」
今でこそこの二つを自然に結びつける事に違和感を感じることは少ないでしょうが, 過去, 特にヨーロッパではこの二つは別モノとして扱われてきました.
つまり
- 数:モノの個数を表すのに使われ,基数とも呼ぶ
- 量:互いに大小が比較出来る長さや大きさなどに使われるモノ
と分けられました.
「量」は同一種でしか比較できないなどの考えもあり, 結果これを改め, 言うならば「現代数学」へと昇華したのは19世紀になってからになります.
対してインドや中国圏ではそう言った概念の別に寛容で, それ故か負数やゼロの存在, 概念としての扱いは比較的古くからなされてきました.
量とは則ち日常に即したものであり, 例えば実数がそうであるように, 数概念を構成するに当たって量の考え方は障壁とも言えます.
…と言うのも, 量には有理数はおろか, 負数, いや  も認められないからです.
も認められないからです.
 の発見の歴史がそうであるように, 量の概念には
の発見の歴史がそうであるように, 量の概念には  すらも想定されていないのです.
すらも想定されていないのです.
これは実数を構成するどころではありません.
とは言っても量を完全に否定するものではありません.
寧ろ数は量の概念があったからこそであり, 言いかえれば「自然数(正整数)から如何に数を拡張するか」が実数へ, そしてその先へと拡張が行われる基礎であることに間違いありません.
そして現代を生きる我々は, もはや量だけでは足りない生活を送っています.
「認める」歴史
我々は既に複素数はもちろん, 実数も有理数も負数も  も, その内容に多少の違いこそあれ認めていることでしょう.
も, その内容に多少の違いこそあれ認めていることでしょう.
「いや, 虚数はそんなことない」と思う方も居られるかもしれませんね.
これまでのヨーロッパでそうだったように, つまるところそれまで
「認めなかったもの」
「存在する訳がないもの」
「有り得ないもの」
をどう認めるか, 納得するか…の繰り返しでした.
逆に言えば数と量を分けて考えた歴史から, それを数と扱うか…について一歩引いてしまっていたのです.
単純な例であれば以下のようなものです.
 なる
なる  は存在するのか
は存在するのか- 存在するとしてもそれを数と認めるべきか
個人が主張しても, 万人が納得しなければ意味がありません.
 にしても負数にしても, その表現や示し方に違いはあれど, その「今でこそ当たり前」に至る苦労は例えるなら地動説天動説の如くでした.
にしても負数にしても, その表現や示し方に違いはあれど, その「今でこそ当たり前」に至る苦労は例えるなら地動説天動説の如くでした.
同時に, 数と量の結びつきについても, 様々な考察を経て今に至ります.
「新しい数」を作る
それまで量に相当する数だけで良かった時代も, 社会の発展や数学そのものの発展により, それでは物足りない事が分かってきました.
全てのシーンにおいてそうではありませんが, 代数学的な流れで行けば
 となる
となる  はないものか…
はないものか…
→
 となる
となる  が必ずしも無い…
が必ずしも無い…
→負数 となる
となる  が必ずしも無い…
が必ずしも無い…
→分数, 有理数
…のように, 量と言う概念に縛られず, 既存の数で対応できない数を埋めるために新しい数が構成されていきました.
もちろん分数, 有理数辺りまでは量概念によって十分構成可能です.
19〜20世紀になりこれらは「同値関係」と言う考え方でより厳密となり, この同値関係は数構成に限らず現代数学の重要な概念の一つとなります.
当然, これに合わせて同値関係では到底構成できない「自然数の定義」も議論の対象となります.
そう言う意味では数概念の厳密な体系化はまだ100年ちょっとしか経っていません.
「当たり前」から新しい数を構成するには比較的容易いですが, 肝心の「当たり前」の何故を解決するそれは後者の比ではないということです.
「あり得ない数」をどう扱うか
結局, 我々はそれを納得するまでその存在を認められませんし, 有り得ないとします.
それはそれで正しいでしょう.
何とか概念として理解しても, その度合いはそれぞれですし, ましてそれを量と統合して見做すなんてことは更に難しいかもしれません.
我々は結局個々人が納得した範囲でしか分からないのかもしれません.
この世界が三次元なのか四次元なのか,もっと次元が大きいのか…と言う(物理科学に寄ってますが)考えも然りです.
観測出来ない数
しかし,ありえないからといって無視してしまうのは勿体ないです.
仮に我々が理解している, 或いは扱っている数を総称して「観測できる数」としましょう.
つまり「あり得ない数」は「観測できない数」です.
良い例として二次方程式の解の公式を考えます, 今は中三で習うでしょうか?
二次方程式の解には実数解でないような実係数の組み合わせが存在する事は周知の事です.
ご存知であればそれが虚数解であることは自明ですね.
しかし解の公式を習う前後ではまだ虚数解…と言うよりそもそも虚数, 複素数を習っていません.
従って彼らには「解なし」と教えます.
つまり彼らにとってはそのような二次方程式の解は「存在しない」し, 「観測できない数」なのです.
しかし複素数を習って間もなく経てば, それは「虚数解として存在する」事を知らされます.
それまで「存在しない」「観測できない数」であったものが突如数として認められるのです.
一時的とはいえ, そんな「観測できない数」が解となりうるようなものを公式としてしまって良いものか, 公式として不完全ではないのか…と疑問に思った方もおられるかもしれません.
結果論的にそれは教育課程上の都合なわけですが, それを知ることのない, 或いは虚数(複素数)を学ぶ際に誤って理解した場合, 当人にとっては「観測できない数」であり続ける可能性が出てきます.
内部対称性
さて, 複素単位は次のように定義されていますね.
 の根の一つ
の根の一つ
ここで件の二次方程式の解は  の二つであることは間違いありません.
の二つであることは間違いありません.
どちらを複素単位とし,  と置くか…が疑問になりますが, 実は「どちらでも良い」が正解です.
と置くか…が疑問になりますが, 実は「どちらでも良い」が正解です.
但し慣例として前者を採用します.
この二つに関わり, 複素数には「複素共役」という関係があることもまたご存知でしょう, つまり
任意の複素数  における
における 
です.
この  と
と  は, 当然複素数の世界から見れば別の数であることは間違いないです.
は, 当然複素数の世界から見れば別の数であることは間違いないです.
しかしこの2つは実数の世界で見れば,  と任意の
と任意の  との違いが分かりません.
との違いが分かりません.
言ってみれば, 実数の世界にいる人には虚数軸やその違いは「見えない」, 「観測できない」のです.
観測できない数を認める事で現時点で観測出来る数体系に問題ないか…は当然疑問視すべきですし確かめる必要があります.
もし問題なければ, 観測できない架空の数であっても, ありえない数であったとしても既存の観測できる数周りの演算などに支障が無ければ十分です.
特にこの複素共役のような関係は内部対称性と呼ばれ, 本来使えない(と解釈されている)はずの物理などで複素数(虚数)が用いられているのはこの内部対称性に基づきます.
先程の数の歴史で言えば, 例えば自然数しか認めなかった時代における負数はまさに「観測できない数」であったのです.
我々は既に負数を数としても扱っていますから, つまり観測できない数はキチンと定義することで観測できる数になりうると言えます.
その意味では, 数学の本質は「ありえない量を如何に数に昇華させ, 統合するか」なのかもしれません.
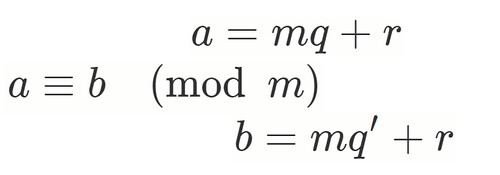
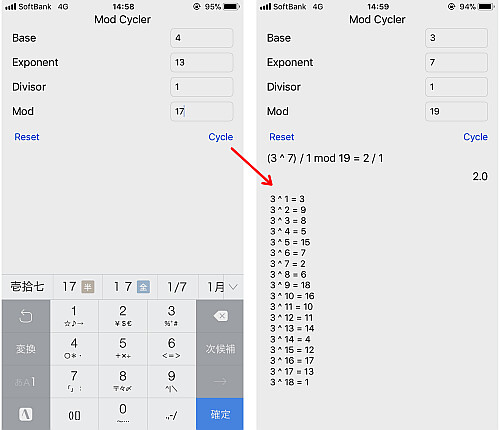
を整数
で割った余りが等しいとき,
と
は (法
に対して)合同であると言います.
を用いて
は
の倍数」を意味します.
は登場しません(依存しない, と言います)から, いちいち余りについて考えることなく合同式を定義できることになります, それが合同式の二つ目の定義です.
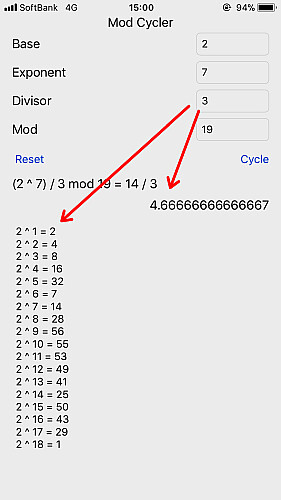
の差
が整数
の倍数であることき,
と
は (法
に対して)合同であると言います.
ならば
をそれぞれ
で割った余りは等しい.
を用いて
…(1)
の組が(ただ一通り)存在して
を
で割った余りが
」となります.
を
で割った余りが
となります.
双方を
で割った余りが共に
で等しくなります.