もう一人のY君

iPhoneアプリのレビューやアップデートレビューなどを書いています. たまに数学の記事も書きます.

もう一人のY君　MENU 　MENU

【数学】自然数、整数、有理数、無理数、実数、複素数

数学

自然数 整数 有理数 無理数 実数 複素数

　今回は数学で馴染みの深いメジャーな数の集まりについてです.

　モノによってはどれがなんだっけ…となるでしょう, その健忘録です.

 

 

スポンサーリンク

 

 

集合と代数系

blog.thetheorier.com

　数学, 特に代数学では集合と, その上に定められている演算や距離をはじめとする「位相」というものは集合が定義されている時点では扱ってない状態なので, 例えば自然数 { \displaystyle \mathbb{N} } とそれに加法を定義した代数系 { \displaystyle (\mathbb{N},+) } は厳密には別モノです.

 

　各々の集合(或いは対象の集まり)に必要な位相を定義することで, はじめてそれらが使えるようになります.

 

 

自然数

　日常生活でも当たり前に使ってる一方, あまりにトリビアルであるように思えてしまうためにどのようにして数学的特徴を捉えるか, それを理解するのは意外と難しく, 現にこれを扱うのは大学数学科以降となります.

 

[公理：ペアノ]

　次の条件を満たす集合 { \displaystyle \mathbb{N} } を自然数と呼ぶ.

 

  1. 1という要素を持つ
  2. { \displaystyle \mathbb{N} } の任意の要素 { \displaystyle x } に対し, { \displaystyle \mathbb{N} } の要素に対応する { \displaystyle x+1 } という規則が定まる({ \displaystyle x } の「次」)
  3. { \displaystyle x+1 = y+1 } ならば { \displaystyle x=y } である(単射)
  4. { \displaystyle x+1=1 } を満たす { \displaystyle x } は存在しない(⇔次が1である数は存在しない)
  5. { \displaystyle \mathbb{N} } は上記 1～4 を満たす最小の集合である

 

　ペアノの公理において, { \displaystyle 1 } という存在はさほど重要ではない…というか, 代わりに { \displaystyle 0 } に置き換えても問題ありません.

　そもそも公理で「{ \displaystyle 1 } とは何ぞや」に触れていないからです.

　但しその場合 { \displaystyle x+1 } と出来ないので代わりに { \displaystyle \text{suc}(x) } (後者を意味するsuccessorの頭3つ)などと表現します.

 

　「手で数えられない」とか「特定のカテゴリでは含めたほうが都合がいい」とか色んな理由で含む, 含まないがありますが, そのくらい曖昧であるということです.

 

　そもそも例えば手をグーにして「{ \displaystyle 0 }」を意味するということにすれば良い気がするんですけどね.

　指を使って{ \displaystyle 2 }進数で数える時だって, 例えば指を曲げる場合を「{ \displaystyle 0 }」を見做すんですから特に違和感を感じません.

 

　そもそもこれがどうして自然数になるのか, 抽象的なのでこれだけでは分かりません.

　例えば { \displaystyle 1+1 } に対応する数は何なのか, 定義により存在することは確かめられますが対応する何らかの(数)記号を用いることが要請されます.

　それを我々は(アラビア数字ならば){ \displaystyle 2 } と書いている, ということです.

　漢数字なら二ですし英語ならtwoですね.

　{ \displaystyle 2 } 以降も同じように何らかの記号を充てがうわけです, その際考えたくなるのが

 

いくつになったら桁上げするのか

 

という問題です.

 

　これによって使用する記号の数が決まり, 各々の数を表現する方法が変わってきます.

　{ \displaystyle 0 } を含め10個ならば10進数, 2個ならば2進数…ということになります.

 

　少なくとも「数学」ではこのように考えます, 指で数える等々も一つの数学ですが, 定義や公理にまで抽象化された概念はもはや「それ」による個々の考え方, 曖昧さを払拭するものとして存在します.

　言い換えれば理解さえすれば言語の別に関係なく万人に共通するということです.

 

 

正整数と非負整数

　上記の通り, 自然数 { \displaystyle \mathbb{N} } に { \displaystyle 0 } を含めるかどうかは大学になっても(意外と数学科であれば尚更)はっきりしません.

 

　そのためこの違いをはっきりさせるため(…なのかは分かりませんが), 正(の)整数と非負整数という集合があります.

　具体的にはそれぞれ

 

{ \displaystyle Z^+ := \{1, 2, 3, 4,\dots\} }

{ \displaystyle \{0, 1, 2, 3, 4,\dots\} }

 

です.

　非負整数については該当する記号を知りません, 無理矢理書くなら { \displaystyle \{0\}\cup Z^+ } でしょうかね(カッコ悪い…).

 

　誤解を与えたくない場合はこの2つを使うと良いでしょう.

 

 

整数

　比較的自然に理解できる自然数ですが, 方程式という「道具」が生まれ, 必然的にある問題が出てきました.

　具体的には例えば

 

 { \displaystyle x+1=0 } となる { \displaystyle x } は何なのか, 存在するのか

 

ということです.

 

　当初は国や地域で様々な考えがなされてきました.

　{ \displaystyle 0 } の概念の歴史背景に同じく「存在しない」とする考え方もありましたし, 同じような方程式の解はいずれも { \displaystyle 0 } とする考えもありました.

(存在しないってことならじゃあ { \displaystyle 0 } の「存在しない」と負数の「存在しない」の違い, もっと言うと虚数もですが…の「存在しない」は同じなの？違うの？どちらの場合もなぜそう言えるの？と, 現在を生きる僕は疑問を覚えるんですけどね. いずれも「存在しない」と仰る方はぜひ教えて欲しいものです, 特に { \displaystyle 0 } と虚数については)

 

　そのため, これに相当する数として(結果的に) { \displaystyle 0 } や負数として今日扱われるようになりました.

 

 

blog.thetheorier.com

　或いは我々は同値関係という画期的なアイデアを知っています.

　自然数から整数, 有理数, また実数から複素数の構成は然るべき同値関係, そして商種集合へ自然な加法・乗法を定めることにより, 各々と同じ構成の代数系を作ることができます

 

 

(蛇足)存在しない数

　今となっては当たり前に使ってる負数(後述する平方根や虚数もですが)は存在しない…という考え方があったのは上の通りです.

　現代でも { \displaystyle 0 } や虚数が存在しない, 実在しない数とする方がおられますが, これは明確な間違いです.

　数は飽くまでも概念であり, 我々はその存在を記号で書いたり喋ったりと何らかの方法でそれを確かめているだけです.

　現に例えば { \displaystyle 0 } だって, 今あなたはそのディプレイから左の記号を見て, それが何であるかを理解しているはずです.

　存在しないならどうしてそれが分かるのでしょう？書けるのでしょうか？

 

blog.thetheorier.com

 

 

分数, 有理数

　方程式を解くにあたって不都合が生じるのは負数だけではありません.

　例えば { \displaystyle 2x=1 } の解は何なのか, これに対応する数は存在するのか…という問題が出てきます.

(このように「方程式を解く」ことをベースに色んな数が必要であることをしみじみと感じさせます)

 

　これを解決するため, 分数や有理数といった概念が生まれました.

 

　分数は2つの数の比を表すのにも使われ, そのため例えば { \displaystyle a : b } という表記とも関連があります, つまり

 

{ \displaystyle a:b = c:d \Leftrightarrow \frac{a}{b}=\frac{c}{d} \Leftrightarrow ad=bc }

 

　という関係があります.

 

blog.thetheorier.com

　分数と有理数については過去に指摘した通りです.

 

 

無理数

　無理数は, つまるところ

 

有理数でない実数

 

と言ってしまえば簡単です.

　このためには実数を理解することが求められることは言うまでもありません.

 

 

小数(有限小数, 無限小数)

　実数に入る前に小数に触れましょう.

　小数は言ってみれば分数を解析的に表現したものです.

　割り算を筆算で解いていった結果と言ってもいいでしょうか.

 

　小数には小数点以下有限で以降 { \displaystyle 0 } となる有限小数と, そうならずひたすら数が並ぶ無限小数があります.

 

　非常にややこしいことに, 以下の図表の通り小数と有理数・無理数は入り組んだ関係となっています.

 

  有限小数  無限小数 
有理数  { \displaystyle \frac{1}{2} }  { \displaystyle \frac{1}{3} } 
無理数   - { \displaystyle \pi } 

(表内の数は具体例)

　面倒ですが理屈から言って間違いではないので仕方ないですね…

 

 

実数

　というわけで実数です.

 

　その前に「稠密(ちゅうみつ)」の話をしましょう.

 

　数はよく一直線上のどこか…といった風に表現します, このとき有理数は数直線上にびっしり敷き詰められているイメージです.

　数学用語でこれを「稠密」と言います, きちんと書けば

 

[稠密性]

　任意の有理数 { \displaystyle a, b (a\lt b) } に対して,

 

{ \displaystyle a\lt p\lt b }

 

を満たす有理数 { \displaystyle p } が存在する.

 

　つまり, それだけ近い(と思った)2つの有理数を取っても, その間にまだ { \displaystyle a, b } とは異なる有理数が, { \displaystyle a } と { \displaystyle b } の間に必ずある…ということです.

 

　稠密は穴が無くビッシリ埋まっているように思えますが実際には無理数というもっとたくさんの数の分だけ隙間があります.

　向こう側は見えないけど水を通す服のようなものですね.

 

　つまりそんな「穴より小さい隙間」をも埋める存在が実数(のうち有理数でないもの)ということになります, 「連続である」と言ってもいいですね.

 

　この「穴より小さい隙間が埋まっている」ことをここでは「完備」と言うのですが, これを公理たらしめる条件は例えば

 

  • 任意のコーシー列が収束する(収束先を実数と定める)
  • { \displaystyle \mathbb{R} } における任意の上に有界な部分集合の下限が { \displaystyle \mathbb{R} } の要素である(任意の下に有界な部分集合の上限が { \displaystyle \mathbb{R} } の要素である)
  • 任意の有界単調数列が収束する

 

…という風に幾つかあります.

 

　これらは互いに同値であるため, どれか一つが確かめられれば十分です.

 

　またここでも例えば { \displaystyle \sqrt2 } に収束する数列などいくらでもあるわけで, これをどう辻褄合わせするか…というと, 先程の整数の項目で触れた「同値関係」の考え方になります.

　分数や有理数もまた, 同じ値で別の表記がいくらでもありますが, それらを同じと見なし, そのグループである「類」を対象とする集まりを考えるわけです.

 

 

 複素数

　実数さえ分かれば複素数は簡単です, つまり実数 { \displaystyle \mathbb{R} } の直積 { \displaystyle \mathbb{R}\times\mathbb{R} } に対して, 次のように加法・乗法を定めれば良いです.

 

{ \displaystyle (a,b) + (c,d) = (a+c,b+d) }

{ \displaystyle (a,b)\times (c,d) := (ac-bd,ad+bc) }

 

　これによる代数系 { \displaystyle (\mathbb{R}\times\mathbb{R}, +, \times ) } が体であることを確認すれば十分です.

　こうして作られた(同じく)同値類 { \displaystyle [a,b] } を { \displaystyle a+bi } と書くことにすれば, 馴染みある複素数と同じものが構成されたことになります.

 

 

虚数と純虚数

　よくどっちがどっちか忘れる典型ですね.

　複素数 { \displaystyle a+bi } のうち, 各々次の場合を言います.

 

  • 虚数：{ \displaystyle b\neq 0 } であるもの
  • 純虚数：{ \displaystyle a=0 } であるもの

 

図表

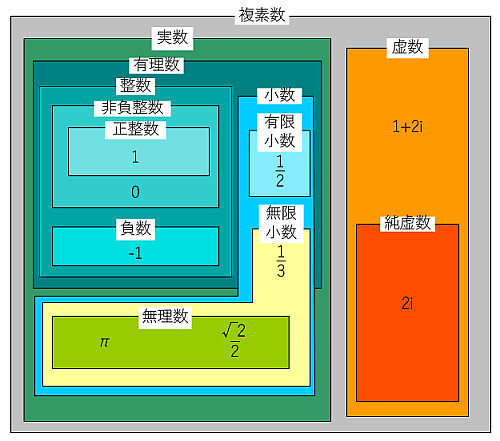
170617_01

　各々を簡単に図表にしたものです, 参考までに.

 

thetheorier